
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление предела в случае неопределенностиСодержание книги
Поиск на нашем сайте Мещерина Е.В.
Методическое пособие по Математике для студентов ветеринарного факультета заочной формы обучения
Оренбург Издательство ОГАУ Содержание Введение……………………………………………………………………….3 §1. Предел функции…………………………………………………………...4 §2. Производная функции. Дифференциал………………………………….8 §3. Исследование функции………………………………………………….11 §4. Интеграл………………………………………………………………….18 Варианты контрольных работ………………………………………………22 Список вопросов к экзамену………………………………………………..38 Список литературы…………………………………………………………..40 Введение В современной науке и технике все большую роль приобретает математическое образование, поскольку в производстве и управлении хозяйством непрерывно возрастает роль математических методов моделирования, проектирования, исследования, планирования. Законы математики – неизменное руководство к безошибочному действию в современной практике ведения хозяйства и изучение их служит подготовке студентов к последующему изучению родственных и специальных курсов. Данное пособие предназначено для студентов ветеринарного факультета заочной формы обучения. В нем представлен теоретический материал по следующим темам: предел функции, производная и дифференциал функции, исследование функции, интеграл. К каждой теме подобраны задачи и представлено их подробное решение. Так же пособие содержит варианты контрольных работ и список вопросов к экзамену по математике. Целью пособия является раскрытие основных методов решения задач по представленным темам. Пособие будет полезно студентам при решении контрольных работ и подготовке к экзамену по математике. Предел функции Определение предела Пусть a – точка числовой прямой, Число A называется пределом функции Число A 1 называется пределом функции f (x) слева в точке a, если для каждого ε > 0 существует δ > 0 такое, что для всех Число A 2 называется пределом функции f (x) справа в точке a, если для каждого ε > 0 существует δ > 0 такое, что для всех Предел слева обозначается Эти пределы характеризуют поведение функции слева и справа от точки a. Их часто называют односторонними пределами. Если для каждого ε > 0 существует такая δ -окрестность точки a, что для всех x, удовлетворяющих условию | x – a | < δ, x ≠ a, выполняется неравенство | f (x)| > ε, то говорят, что функция f (x) имеет в точке a бесконечный предел: Если для каждого ε > 0 существует такое δ > 0, что для любого x > δ выполняется неравенство | f (x) – A | < ε, то говорят, что предел функции f (x) при x, стремящемся к плюс бесконечности, равен A: Аналогично формулируется определение предела при x, стремящемся к минус бесконечности: Пример 1. а) б) в) г) Свойства пределов Если существует 1) 2) 3) 4) Теорема: Если в некоторой окрестности точки а выполняется неравенство Пример 2. Найти Решение. Пользуясь свойствами пределов получаем, что
Пример 3. Найти Решение. Пользуясь свойствами пределов получаем, что
Замечание. В дальнейшем будем пользоваться тем, что для любой элементарной функции f (x) и любой точки а из ее области определения справедливо соотношение Бесконечно большая функция Определение. Функция f (x) называется бесконечно большой при
Определение. Функция f (x) называется бесконечно малой при
Сформулируем основные соотношения для бесконечно больших и бесконечно малых функций. Если Если Если Если Если Если Пример 4. Найти Решение. Пользуясь свойствами пределов, получаем:
Так как
Производная Определение производной Рассмотрим функцию Определение. Разность Определение. Разность Определение. Если существует предел отношения приращения функции к приращению аргумента, при условии, что приращение аргумента стремится к 0, то его называют производной функции в точке
Нахождение производной называется дифференцированием функции. Геометрический смысл производной состоит в том, что производная есть угловой коэффициент касательной к графику функции Правила дифференцирования 1. 2. 3. 4. 5. Пример 1. Найти производную функции Решение.
Пример 2. Найти производную функции Решение.
Пример 3. Найти производную функции Решение.
Пример 4. Найти производную функции Решение.
Производная сложной функции Пусть функция
Таким образом, производная сложной функции равна произведению производных функций ее составляющих Пример 5. Найти производную функции Решение. Обозначим
откуда
Пример 6. Найти производную функции Решение. Обозначим
Определение. Производной второго порядка функции
Определение. Производной n-го порядка функции
Дифференциал функции Определение. Линейную функцию
Дифференциал функции используют в приближенных вычислениях:
Геометрический смысл дифференциала: дифференциал функции Пример 7. Вычислить дифференциал функции Решение.
Свойства функции Четность, нечетность. Определение. Множество D называют симметричным относительно начала координат, если для любого х Определение. Функцию f (x), заданную на множестве D (f), называют четной (нечетной), если: 1) множество D (f) симметрично относительно начала координат; 2) для любого х Функцию, которая не является ни четной, ни нечетной, называют функцией общего вида. Пример 1. Исследуем на четность функцию Решение. Сразу можно сделать вывод, что имеем функцию общего вида, так как ее область определения Пример 2. Исследуем на четность функцию f (x) = x 2 + Решение. 1) Df = ( 2) Составим выражение для f ( f ( Вывод: Так как f ( Периодичность. Определение. Функцию у = f (x), заданную на множестве D (f), называют периодической, если существует такое число Т ≠ 0, что: 1) для любого числа х, принадлежащего области определения функции Df, числа х ± Т также принадлежат области определения. ( (отсюда следует неограниченность области определения) 2) для всякого числа х из области определения справедливо равенство f (х ± Т) = f (x). Число Т называют периодом функции. Например, f (x) = cos x, T = 2π. Возрастание и убывание. Рассмотрим функцию y = f (x), заданную на множестве D (f). Пусть х 1 и х 2 – любые две различные точки множества (например, х 1 < x 2), содержащегося во множестве D (f). Определение. Функцию y = f (x) называют на множестве Х – возрастающей, если – убывающей, если – невозрастающе й, если – неубывающей, если Во всех четырех случаях функцию называют монотонной на множестве Х. Теорема. Для того чтобы дифференцируемая на промежутке Х функция y = f (x) была возрастающей (убывающей) на этом промежутке, необходимо и достаточно, чтобы для любого
Пример 3. Найти промежутки монотонности функции Решение. Найдем производную данной функции
Найдем точки, в которых производная равна 0 и не существует, то есть решим уравнение
Следовательно, производная равна 0 при
Наносим эти точки на координатную прямую и расставляем знаки производной в каждом полученном интервале Пользуясь предыдущей теоремой, получаем: функция возрастает на промежутках, где производная положительна, то есть на промежутках Экстремумы функции. Определение. Точку Другими словами, точка Определение. Точки максимума и минимума называют точками экстремума функции, а значения функции в этих точках называют экстремумами функции.
Признак экстремума: Если функция y = f (x) возрастает (убывает) на некотором интервале  , содержащемся в D (f) и убывает (возрастает) на интервале , содержащемся в D (f) и убывает (возрастает) на интервале  , содержащемся в D (f), то точка , содержащемся в D (f), то точка   точка локального максимума (минимума) функции y = f (x). точка локального максимума (минимума) функции y = f (x).
Пример 4. Найдем промежутки монотонности и экстремумы функции Решение. Функция определена, непрерывна и нечетна на промежутке 1. Найдем критические точки, то есть точки, в которых производная
Точки х = 0, х = 1, х = 2.
Функция убывает на лучах
Асимптоты графика функции. Прямая
Прямая 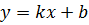 называется наклонной асимптотой графика функции называется наклонной асимптотой графика функции  . .
При Аналогично определяются асимптоты при Прямая Прямая Пример 6. Найти асимптоты графика функции Решение. Найдем
поэтому Функция не определена в точке
Таким образом, Замечание. Асимптота графика функции может пересекать сам график. Горизонтальные и наклонные асимптоты графика функции 1. Вычислить 2. Вычислить 3. Вычислить 4. Записать уравнение наклонной асимптоты: Пример 7. Исследовать функцию Решение. Обратимся к схеме исследования функции. 1. Найдем область определения функции. Так как функция задана дробным выражением, то знаменатель этой дроби должен быть отличен от 0. То есть 2. Точка
3. Найдем точки пересечения графика функции с осью Оу, то есть при Найдем точки пересечения графика функции с осью Ох, то есть при 4. Найдем промежутки знакопостоянства функции
Получили что на промежутках 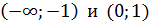 функция отрицательна, а на промежутках функция отрицательна, а на промежутках  – положительна. – положительна.
5. 1) Область определения функции – симметричное относительно начала координат множество. 2) Найдем
Получили что Из 1) и 2) следует, что функция нечетная. Функция не является периодической. 6. Для того чтобы найти промежутки монотонности функции, необходимо найти производную
и решить уравнение
При  производная не существует. Отметим эту точку на координатной прямой и расставим знаки производной на каждом полученном интервале. производная не существует. Отметим эту точку на координатной прямой и расставим знаки производной на каждом полученном интервале.
Значит, функция возрастает на каждом из промежутков 7. Экстремумов нет, так как производная не обращается в 0. 8. Чтобы определить промежутки выпуклости функции, нужно найти производную второго порядка от этой функции
и решить уравнение
Данное уравнение решений не имеет. Найдем точки, в которых производная второго порядка не существует. Это точка
Нанесем эту точку на координатную прямую и расставим знаки второй производной в каждом полученном интервале Значит, график функции выпуклый вниз на промежутке 9. Найдем асимптоты графика функции. Точка
Значит, Найдем так же
Исследуем функцию на наличие наклонных асимптот. Для этого найдем предел
Следовательно, прямая Найдем
Следовательно, прямая
 . .
10. Построим график функции.
Интеграл Неопределенный интеграл Определение. Функция Пример 1. Функция Определение. Множество всех первообразных Пример 2. а) б) Таблица основных неопределенных интегралов 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) Определенный интеграл Пусть функция Разобьем отрезок Обозначим | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 . Пусть функция
. Пусть функция  определена на множестве
определена на множестве  .
. при х, стремящемся к а (обозначается
при х, стремящемся к а (обозначается  ), если для любого положительного числа
), если для любого положительного числа 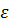 (
( существует такое положительное число
существует такое положительное число  что для любого
что для любого  такого, что
такого, что  , выполнено неравенство
, выполнено неравенство  .
. выполняется неравенство
выполняется неравенство 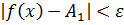 .
. выполняется неравенство
выполняется неравенство  .
. предел справа –
предел справа –  .
.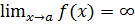
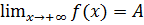 .
. .
. ;
; ;
; ;
; .
. и существует
и существует  , то:
, то: ;
; ;
; ;
; .
. и
и  , то
, то  .
. .
. .
.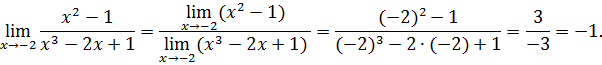
 .
. , если для любого положительного числа С существует окрестность точки а такая, что
, если для любого положительного числа С существует окрестность точки а такая, что  для любого х из выбранной окрестности точки а и принадлежащего области определения функции f (x). Обозначение
для любого х из выбранной окрестности точки а и принадлежащего области определения функции f (x). Обозначение .
.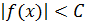 для любого х из выбранной окрестности точки а и принадлежащего области определения функции f (x). Обозначение
для любого х из выбранной окрестности точки а и принадлежащего области определения функции f (x). Обозначение .
. то
то  , и обратно, если
, и обратно, если  .
. и
и  , то
, то  .
.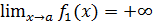 и
и  , то
, то  .
. , то
, то  .
. и
и  , то
, то  .
. и
и 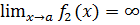 , то
, то  .
. .
. .
. то
то  . Тогда
. Тогда .
. , определенную на некотором интервале
, определенную на некотором интервале  .
. называют приращением аргумента х в точке х 0.
называют приращением аргумента х в точке х 0.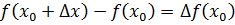 называют приращением функции f (x) в точке х 0.
называют приращением функции f (x) в точке х 0. и обозначают
и обозначают 
 .
.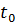 ; биологический смысл: если зависимость между числом особей популяции микроорганизмов y и временем t ее размножения задана уравнением y = p (t), то
; биологический смысл: если зависимость между числом особей популяции микроорганизмов y и временем t ее размножения задана уравнением y = p (t), то  – производительность жизнедеятельности популяции микроорганизмов в момент времени t.
– производительность жизнедеятельности популяции микроорганизмов в момент времени t. ;
; ;
; ;
; ;
; .
. .
.
 .
. .
. .
.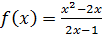 .
. =
= 
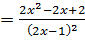 .
. .
.
 .
. имеет производную в некоторой точке
имеет производную в некоторой точке 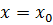 , а функция
, а функция  имеет производную в точке
имеет производную в точке  . Тогда, сложная функция
. Тогда, сложная функция 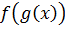 имеет производную в точке
имеет производную в точке  .
. .
. .
. . По правилу нахождения производной сложной функции
. По правилу нахождения производной сложной функции  ,
, .
. .
. , тогда
, тогда  . По правилу нахождения производной сложной функции
. По правилу нахождения производной сложной функции  .
. .
. .
. .
.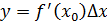 называют дифференциалом функции f в точке
называют дифференциалом функции f в точке  . Поэтому пишут:
. Поэтому пишут:  . Отсюда
. Отсюда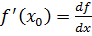 .
.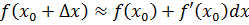 .
. есть приращение ординаты касательной, проведенной к графику функции в точку с абсциссой
есть приращение ординаты касательной, проведенной к графику функции в точку с абсциссой  .
.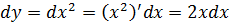 .
.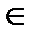 D противоположное ему число (
D противоположное ему число ( .
. не симметрична относительно начала координат.
не симметрична относительно начала координат. +
+  .
. (0;+ ∞) – симметричное множество относительно точки О (0; 0).
(0;+ ∞) – симметричное множество относительно точки О (0; 0). +
+  = x 2 +
= x 2 + 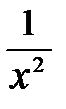 +
+  = f (x)
= f (x) x
x  +
+ 
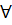 х
х  Df)
Df)  (х ± Т
(х ± Т 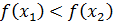 (меньшему значению аргумента соответствует меньшее значение функции);
(меньшему значению аргумента соответствует меньшее значение функции); (меньшему значению аргумента соответствует большее значение функции);
(меньшему значению аргумента соответствует большее значение функции);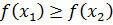 ;
;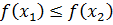 .
.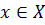 выполнялось условие
выполнялось условие 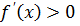
 .
. .
. .
. .
.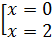 , а не существует при
, а не существует при  .
. и убывает на промежутках, где производная отрицательна, то есть на промежутках
и убывает на промежутках, где производная отрицательна, то есть на промежутках  .
.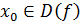 называют точкой максимума (минимума) функции y = f (x) с областью определения D (f), если существует интервал
называют точкой максимума (минимума) функции y = f (x) с областью определения D (f), если существует интервал 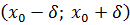 , где
, где 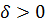 , содержащийся в D (f), такой, что для каждого
, содержащийся в D (f), такой, что для каждого  из этого интервала выполняется неравенство
из этого интервала выполняется неравенство 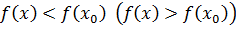 .
.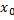


 .
. .
. либо не существует, либо равна 0.
либо не существует, либо равна 0.
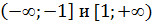 , возрастает на отрезке [
, возрастает на отрезке [ 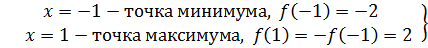 экстремумы функции.
экстремумы функции. равен
равен  .
.
 наклонная асимптота называется горизонтальной.
наклонная асимптота называется горизонтальной. и при
и при  .
. .
. .
. .
. ,
, – горизонтальная асимптота графика данной функции.
– горизонтальная асимптота графика данной функции. ,
, можно находить по следующему алгоритму.
можно находить по следующему алгоритму. . Если этот предел существует и равен некоторому числу с, то
. Если этот предел существует и равен некоторому числу с, то  – горизонтальная асимптота. Если предел не существует или равен бесконечности, то следует перейти ко второму пункту.
– горизонтальная асимптота. Если предел не существует или равен бесконечности, то следует перейти ко второму пункту.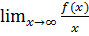 . Если этот предел не существует или равен бесконечности, то асимптоты нет. Если существует конечный предел
. Если этот предел не существует или равен бесконечности, то асимптоты нет. Если существует конечный предел  , то следует перейти к третьему шагу.
, то следует перейти к третьему шагу. . Если этот предел не существует или равен бесконечности, то асимптоты нет. Если существует конечный предел
. Если этот предел не существует или равен бесконечности, то асимптоты нет. Если существует конечный предел  , то следует перейти к четвертому шагу.
, то следует перейти к четвертому шагу. и построить ее график.
и построить ее график. 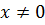 . Значит,
. Значит,  .
. :
: .
. .
. :
:  .
. .
. .
.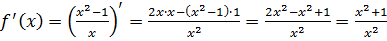
 .
. .
.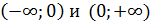 .
.
 .
. , вверх на
, вверх на  .
. .
.
 .
.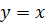 – наклонная асимптота графика функции при
– наклонная асимптота графика функции при 
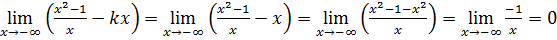 .
. называется перевообразной для функции
называется перевообразной для функции  , если для любого
, если для любого  .
. является первообразной для функции
является первообразной для функции  , так как
, так как  . Функция
. Функция 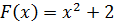 тоже является первообразной для функции
тоже является первообразной для функции  . Функция
. Функция  тоже является первообразной для функции
тоже является первообразной для функции  . Таким образом, множество всех первообразных для функции
. Таким образом, множество всех первообразных для функции  выглядит так:
выглядит так:  , где
, где  – некоторая постоянная.
– некоторая постоянная. для функции
для функции  называют неопределенным интегралом и обозначают
называют неопределенным интегралом и обозначают  .
.  называется подинтегральной функцией,
называется подинтегральной функцией,  – подинтегральным выражением,
– подинтегральным выражением, 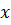 – переменной интегрирования.
– переменной интегрирования. .
. .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. и принимает на нем неотрицательные значения.
и принимает на нем неотрицательные значения. .
. разность
разность 


