
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая схема исследования функцииСодержание книги
Поиск на нашем сайте 1. Найти область определения функции. 2. Определить поведение функции на границах области определения. 3. Найти точки пересечения графика функции с осями координат. 4. Найти промежутки знакопостоянства. 5. Исследовать функцию на четность и периодичность. 6. Найти промежутки монотонности функции. 7. Найти экстремумы функции. 8. Найти промежутки выпуклости и точки перегиба графика функции. 9. Исследовать функцию на существование вертикальных, горизонтальных и наклонных асимптот. 10. Построить график функции. Определение. Областью определения D (y) функции у = f (x) (если это не оговорено особо) называют множество всех значений независимой переменной х, при которых выполнимы все операции, указанные формулой. Определение. Известно, что под множеством значений функции Свойства функции Четность, нечетность. Определение. Множество D называют симметричным относительно начала координат, если для любого х Определение. Функцию f (x), заданную на множестве D (f), называют четной (нечетной), если: 1) множество D (f) симметрично относительно начала координат; 2) для любого х Функцию, которая не является ни четной, ни нечетной, называют функцией общего вида. Пример 1. Исследуем на четность функцию Решение. Сразу можно сделать вывод, что имеем функцию общего вида, так как ее область определения Пример 2. Исследуем на четность функцию f (x) = x 2 + Решение. 1) Df = ( 2) Составим выражение для f ( f ( Вывод: Так как f ( Периодичность. Определение. Функцию у = f (x), заданную на множестве D (f), называют периодической, если существует такое число Т ≠ 0, что: 1) для любого числа х, принадлежащего области определения функции Df, числа х ± Т также принадлежат области определения. ( (отсюда следует неограниченность области определения) 2) для всякого числа х из области определения справедливо равенство f (х ± Т) = f (x). Число Т называют периодом функции. Например, f (x) = cos x, T = 2π. Возрастание и убывание. Рассмотрим функцию y = f (x), заданную на множестве D (f). Пусть х 1 и х 2 – любые две различные точки множества (например, х 1 < x 2), содержащегося во множестве D (f). Определение. Функцию y = f (x) называют на множестве Х – возрастающей, если – убывающей, если – невозрастающе й, если – неубывающей, если Во всех четырех случаях функцию называют монотонной на множестве Х. Теорема. Для того чтобы дифференцируемая на промежутке Х функция y = f (x) была возрастающей (убывающей) на этом промежутке, необходимо и достаточно, чтобы для любого
Пример 3. Найти промежутки монотонности функции Решение. Найдем производную данной функции
Найдем точки, в которых производная равна 0 и не существует, то есть решим уравнение
Следовательно, производная равна 0 при
Наносим эти точки на координатную прямую и расставляем знаки производной в каждом полученном интервале Пользуясь предыдущей теоремой, получаем: функция возрастает на промежутках, где производная положительна, то есть на промежутках Экстремумы функции. Определение. Точку Другими словами, точка Определение. Точки максимума и минимума называют точками экстремума функции, а значения функции в этих точках называют экстремумами функции.
Признак экстремума: Если функция y = f (x) возрастает (убывает) на некотором интервале  , содержащемся в D (f) и убывает (возрастает) на интервале , содержащемся в D (f) и убывает (возрастает) на интервале  , содержащемся в D (f), то точка , содержащемся в D (f), то точка   точка локального максимума (минимума) функции y = f (x). точка локального максимума (минимума) функции y = f (x).
Пример 4. Найдем промежутки монотонности и экстремумы функции Решение. Функция определена, непрерывна и нечетна на промежутке 1. Найдем критические точки, то есть точки, в которых производная
Точки х = 0, х = 1, х = 2.
Функция убывает на лучах
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 568; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 понимают множество всех таких чисел у 0, для каждого из которых существует число
понимают множество всех таких чисел у 0, для каждого из которых существует число 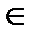 D противоположное ему число (
D противоположное ему число ( .
. не симметрична относительно начала координат.
не симметрична относительно начала координат. +
+  .
. (0;+ ∞) – симметричное множество относительно точки О (0; 0).
(0;+ ∞) – симметричное множество относительно точки О (0; 0). +
+  = x 2 +
= x 2 + 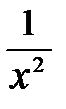 +
+  = f (x)
= f (x) x
x  +
+ 
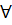 х
х  Df)
Df)  (х ± Т
(х ± Т 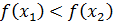 (меньшему значению аргумента соответствует меньшее значение функции);
(меньшему значению аргумента соответствует меньшее значение функции); (меньшему значению аргумента соответствует большее значение функции);
(меньшему значению аргумента соответствует большее значение функции);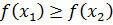 ;
;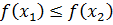 .
.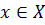 выполнялось условие
выполнялось условие 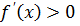
 .
. .
. .
. .
.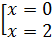 , а не существует при
, а не существует при  .
. и убывает на промежутках, где производная отрицательна, то есть на промежутках
и убывает на промежутках, где производная отрицательна, то есть на промежутках  .
.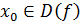 называют точкой максимума (минимума) функции y = f (x) с областью определения D (f), если существует интервал
называют точкой максимума (минимума) функции y = f (x) с областью определения D (f), если существует интервал 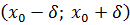 , где
, где 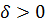 , содержащийся в D (f), такой, что для каждого
, содержащийся в D (f), такой, что для каждого  из этого интервала выполняется неравенство
из этого интервала выполняется неравенство 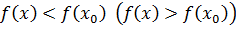 .
.
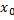


 .
. .
. либо не существует, либо равна 0.
либо не существует, либо равна 0.
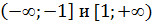 , возрастает на отрезке [
, возрастает на отрезке [ 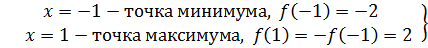 экстремумы функции.
экстремумы функции.


