
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение производной к исследованию функции.Содержание книги
Поиск на нашем сайте
Построение графиков функций [5],гл.2; [3],т.1,гл.5; [8],гл.7,§2; [9],гл.3; [10]
Промежутки монотонности и точки экстремума функции
Чтобы определить промежутки возрастания и убывания функции Чтобы найти точки экстремума (максимума или минимума) функции у (х), прежде всего определяют критические точки функции у (х), то есть точки, входящие в множество определения функции, в которых выполняется необходимое условие экстремума: либо у' (х)= 0, либо у' (х) = ∞, либо у' (х)не существует. Затем каждую из найденных критических точек проверяют на наличие экстремума с помощью одного из достаточных признаков существования экстремума (по первой или второй производной). Пример 32. Найти промежутки монотонности и точки экстремума функции, Решение: Прежде всего отметим, что данная функция определена на всей числовой оси, кроме точки х = 1. Продифференцируем эту функцию
Очевидно, что точка В критических точках Найдем экстремальные значения функции:
Выпуклость и вогнутость графика Функции. Точки перегиба
Промежутки выпуклости и вогнутости графика функции, а также точки перегиба определяются с помощью второй производной у". На промежутках выпуклости у" < 0, на промежутках вогнутости у" > 0. Чтобы найти точки перегиба, исследуют точки, в которых либо у" = 0, либо у" = Пример 33. Найти промежутки выпуклости и вогнутости, а также точки перегиба функции Решение: Зная первую производную
Поскольку первая производная в точке Асимптоты графика функции
а)Прямая х = а является вертикальной асимптотой графика функции у(х), если хотя бы один из односторонних пределов: Пример 34. Найти вертикальные асимптоты графика функции Решение: Как отмечалось, данная функция не определена в точке
Поэтому прямая х = 1является вертикальной асимптотой графика заданной функции. б) График функции у(х) имеет наклонную асимптоту у = kx + b при Пример 35. Найти наклонные асимптоты графика функции Решение: Найдем значения к и b для данной функции при
Аналогично находим, что при 4.3.7. Общий план исследования функции Чтобы составить достаточно полное представление о характере поведения функции и построить ее график, удобно проводить ее исследование по следующему плану: 1. Установить множество определения функции; при наличии точек разрыва найти в них односторонние пределы данной функции; 2.а) Найти точки пересечения графика функции с осями координат, б) Отметить особенности графика заданной функции, не связанные с производными, например, симметрию, периодичность. 3. Установить промежутки возрастания и убывания функции, найти ее экстремумы. 4. Установить промежутки выпуклости и вогнутости график функции, найти точки перегиба. 5 Найти асимптоты графика функции. Пример 36. Исследовать функцию Решение: Как отмечалось в примере 32, множество определения данной функции - вся числовая ось Ох, исключая точку Пример 37. Исследовать функцию Решение: 1. Множество определения данной функции - вся числовая ось Ох, кроме точки
2. а) Точки пересечения графика функции с осью Ох определяются из условия у = 0. В данном случае уравнение б) Поскольку 3. Находим
Производная у' существует и конечна на всем множестве определения заданной функции Функция Функция 4. Находим Вторая производная существует и конечна во всех точках множества определения данной функции. Тогда все точки перегиба находим из условия: у" = 0, то есть 5. Как было установлено в пункте 1, в точке х = 0 функция
Значит, прямая у = x+ 1является наклонной асимптотой графика функции при Пример 38. Исследовать функцию Решение: 1). Данная функция определена на всей числовой
2). Точки пересечения графика функции с осью Ох определяются из условия 3). 4).
Таким образом, наклонные асимптоты также отсутствуют. На рис.15 схематически изображен график функции Комплексные числа [6],гл.1,§6; [3],гл.7,§§1,2,3
Выражение Операции сложения и умножения комплексных чисел в алгебраической форме можно выполнять по обычным правилам алгебры многочленов, если учесть, что Пример 39. Найти вещественную и мнимую части комплексного числа
Решение: Чтобы упростить запись данного комплексного числа, учтем, что
Умножим числитель и знаменатель второй дроби на число, сопряженное знаменателю, и выполним очевидные преобразования:
Значит, Rez = Пример 40. Представить в тригонометрической форме и изобразить на комплексной плоскости число Решение: Изобразим комплексное число z = 1- i точкой М на комплексной плоскости, откладывая по оси Ох его вещественную часть Rez = 1, а по оси Оу мнимую часть Imz = -1. Радиус-вектор ОМ составляет с осью Ох угол
В данном случае
Итак,
Неопределенный интеграл [6],гл.1; [7],гл.1;[3],т.1,гл.10; [8],гл.9; [9],гл.4, [10]
Интегрирование - нахождение функции по ее дифференциалу - это математическая операция, обратная дифференцированию функции. В то время, когда дифференцирование функции проводится на основании общего правила, вытекающего из определения производной, для интегрирования функции нельзя указать такие общие правила. Техника интегрирования основана на применении основных свойств неопределенного интеграла и таблицы основных интегралов.
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 504; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.43 (0.008 с.) |

 , а также ее точки экстремума, надо вначале найти первую производную у' (х)заданной функции. Затем следует определить промежутки, на которых эта производная сохраняет свой знак: там, где у' (х)> 0, функция у (х) возрастает; если же у' (х) < 0, то на этом промежутке функция у (х)убывает.
, а также ее точки экстремума, надо вначале найти первую производную у' (х)заданной функции. Затем следует определить промежутки, на которых эта производная сохраняет свой знак: там, где у' (х)> 0, функция у (х) возрастает; если же у' (х) < 0, то на этом промежутке функция у (х)убывает.
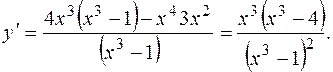
 не является критической, поскольку не принадлежит множеству определения функции. Имеем две критические точки, в которых
не является критической, поскольку не принадлежит множеству определения функции. Имеем две критические точки, в которых  Чтобы найти промежутки возрастания функции у (х),надо решить неравенство у' > 0, или
Чтобы найти промежутки возрастания функции у (х),надо решить неравенство у' > 0, или  Оно выполняется при
Оно выполняется при  - это промежутки возрастания функции. Соответственно, у' < 0 при
- это промежутки возрастания функции. Соответственно, у' < 0 при  - промежутки убывания данной функции.
- промежутки убывания данной функции. проверим выполнение достаточного условия существования экстремума с использованием первой производной. При переходе через точку х = 0 первая производная у' меняет знак с (+) на (-), значит, х = 0 - точка максимума. Аналогично, точка
проверим выполнение достаточного условия существования экстремума с использованием первой производной. При переходе через точку х = 0 первая производная у' меняет знак с (+) на (-), значит, х = 0 - точка максимума. Аналогично, точка 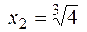 - точка минимума, потому что при переходе через нее первая производная
- точка минимума, потому что при переходе через нее первая производная  меняет знак с (-) на (+).
меняет знак с (-) на (+).
 , либо у" не существует (причем в последних двух случаях у' в соответствующих точках определена). Точками перегиба являются те из найденных точек, при переходе через которые у" изменяет свой знак.
, либо у" не существует (причем в последних двух случаях у' в соответствующих точках определена). Точками перегиба являются те из найденных точек, при переходе через которые у" изменяет свой знак. , найдем вторую
, найдем вторую
 - это точка перегиба, поскольку при переходе через нее у" меняет свой знак с (+) на (-). Промежутки вогнутости графика данной функции:
- это точка перегиба, поскольку при переходе через нее у" меняет свой знак с (+) на (-). Промежутки вогнутости графика данной функции:  , на промежутке
, на промежутке  график функции выпуклый. Значение функции в точке перегиба:
график функции выпуклый. Значение функции в точке перегиба: 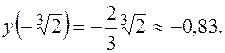
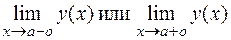 обращается в бесконечность. Поэтому для отыскания вертикальных асимптот графика функции надо найти точки бесконечного разрыва данной функции, которые относятся к точкам разрыва 2-го рода.
обращается в бесконечность. Поэтому для отыскания вертикальных асимптот графика функции надо найти точки бесконечного разрыва данной функции, которые относятся к точкам разрыва 2-го рода.
 , если существуют конечные пределы:
, если существуют конечные пределы:  Если хотя бы один из этих пределов не существует или бесконечен, то график функции не имеет наклонной асимптоты при
Если хотя бы один из этих пределов не существует или бесконечен, то график функции не имеет наклонной асимптоты при 

 по-прежнему
по-прежнему  . Таким образом, график функции
. Таким образом, график функции  имеет одну и ту же наклонную асимптоту при
имеет одну и ту же наклонную асимптоту при 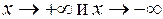 ; это прямая у = х.
; это прямая у = х. График функции пересекается с осями координат в единственной точке 0(0,0). Функция не является ни четной, ни нечетной, поскольку
График функции пересекается с осями координат в единственной точке 0(0,0). Функция не является ни четной, ни нечетной, поскольку 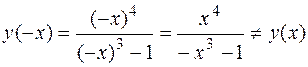 и
и  ,поэтому график функции не обладает свойствами симметрии. Дальнейшее исследование этой функции фактически уже проведено в примерах 32 -35. По данным, полученным в этих примерах, сделан схематический чертеж графика заданной функции, который представлен на рис.13.
,поэтому график функции не обладает свойствами симметрии. Дальнейшее исследование этой функции фактически уже проведено в примерах 32 -35. По данным, полученным в этих примерах, сделан схематический чертеж графика заданной функции, который представлен на рис.13. и сделать схематический чертеж ее графика.
и сделать схематический чертеж ее графика. . Найдем односторонние пределы функции при
. Найдем односторонние пределы функции при  . Предел слева
. Предел слева  так как
так как  и
и  . При вычислении предела справа возникает неопределенность вида
. При вычислении предела справа возникает неопределенность вида  ; приводим ее к неопределенности вида
; приводим ее к неопределенности вида  , к которой применяем правило Лопиталя:
, к которой применяем правило Лопиталя:

 не имеет решений, так как х = 0 не входит в множество определения функции. Точки пересечения графика функции с осью Оу можно найти, положив х = 0. Для заданной функции это значение не входит в множество ее определения. Следовательно, график исследуемой функции не имеет точек пересечения с осями координат.
не имеет решений, так как х = 0 не входит в множество определения функции. Точки пересечения графика функции с осью Оу можно найти, положив х = 0. Для заданной функции это значение не входит в множество ее определения. Следовательно, график исследуемой функции не имеет точек пересечения с осями координат. , то функция не является ни четной, ни нечетной.
, то функция не является ни четной, ни нечетной.
 . Поскольку точка разрыва первой производной х = 0 не принадлежит множеству определения функции, то все критические точки функции
. Поскольку точка разрыва первой производной х = 0 не принадлежит множеству определения функции, то все критические точки функции  находим из условия:
находим из условия: 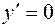 , или
, или 
 . Отсюда получаем
. Отсюда получаем  .
. , то есть при
, то есть при 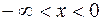 и
и  .
. , в данном случае при
, в данном случае при  Таким образом, при переходе через точку
Таким образом, при переходе через точку 

 . Поскольку это уравнение не имеет решения, то точек перегиба нет. График функции - выпуклый, если у" < 0; в данном случае при х < 0. График функции вогнутый при x> 0; > 0, где у" > 0.
. Поскольку это уравнение не имеет решения, то точек перегиба нет. График функции - выпуклый, если у" < 0; в данном случае при х < 0. График функции вогнутый при x> 0; > 0, где у" > 0.

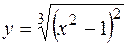 и сделать схематический чертеж графика.
и сделать схематический чертеж графика. оси
оси 
 , откуда
, откуда  , а с осью
, а с осью  - из условия
- из условия  , при этом
, при этом  . Данная функция - четная, поскольку
. Данная функция - четная, поскольку  , значит, ее график симметричен относительно оси
, значит, ее график симметричен относительно оси  . Первая производная обращается в бесконечность в точках х = 1, х = -1, в то время, как сама функция
. Первая производная обращается в бесконечность в точках х = 1, х = -1, в то время, как сама функция  и
и  . Функция возрастает при у' > 0, то есть при -1 < х < 0 и при х > 1. Таким образом, х = 0 -точка максимума,
. Функция возрастает при у' > 0, то есть при -1 < х < 0 и при х > 1. Таким образом, х = 0 -точка максимума,  и
и  - точки минимума данной функции;
- точки минимума данной функции;  ;
;  В точках х = -1 и х = 1 данная функция имеет так называемый "острый" экстремум: касательная к графику функции в каждой из этих точек параллельна оси Оу.
В точках х = -1 и х = 1 данная функция имеет так называемый "острый" экстремум: касательная к графику функции в каждой из этих точек параллельна оси Оу.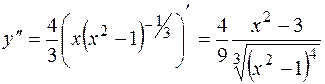 . Вторая производная обращается в бесконечность при х = ±1, но эти точки не принадлежат множеству определения у' (х)и, следовательно, не являются критическими точками для первой производной. Значит, критические точки для нее определяем из условия у" = 0, откуда
. Вторая производная обращается в бесконечность при х = ±1, но эти точки не принадлежат множеству определения у' (х)и, следовательно, не являются критическими точками для первой производной. Значит, критические точки для нее определяем из условия у" = 0, откуда 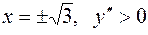 при
при  то график у (х)в этих интервалах вогнутый, а в интервалах
то график у (х)в этих интервалах вогнутый, а в интервалах 

 - график выпуклый, так как там у" < 0.
- график выпуклый, так как там у" < 0.
 5). Поскольку функция определена на всей числовой оси Ox, то вертикальных асимптот у ее графика нет. Проверим наличие наклонных асимптот:
5). Поскольку функция определена на всей числовой оси Ox, то вертикальных асимптот у ее графика нет. Проверим наличие наклонных асимптот:
 называется алгебраической формой комплексного числа z, если а и b - вещественные числа, а
называется алгебраической формой комплексного числа z, если а и b - вещественные числа, а  . Комплексное число i называется мнимой единицей, число а - вещественной частью комплексного числа z, число b - мнимой частью этого числа. Обозначается: а = Rez, b = Imz. Число bi называют чисто мнимым числом.
. Комплексное число i называется мнимой единицей, число а - вещественной частью комплексного числа z, число b - мнимой частью этого числа. Обозначается: а = Rez, b = Imz. Число bi называют чисто мнимым числом. и вообще
и вообще  . Число
. Число  называется сопряженным комплексному числу. Очевидно,
называется сопряженным комплексному числу. Очевидно,  .
. .
.


 ; Imz = - 1.
; Imz = - 1. .
. , называемый аргументом комплексного числа
, называемый аргументом комплексного числа  инаходится с помощью формул
инаходится с помощью формул
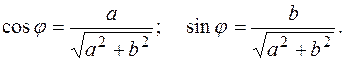
 Значит
Значит  . Модулем комплексного числа z = а + bi называется длина радиуса-вектора
. Модулем комплексного числа z = а + bi называется длина радиуса-вектора  В нашем примере
В нашем примере  Тригонометрической формой комплексного числа z = а + bi называется выражение
Тригонометрической формой комплексного числа z = а + bi называется выражение
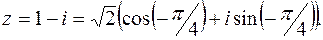 (см. рис.16)
(см. рис.16)


