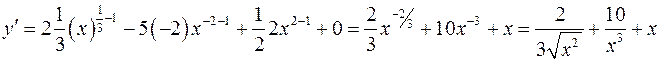Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление пределов с использованиемСодержание книги
Поиск на нашем сайте
Эквивалентных бесконечно малых величин
Функции
Пример 17. Найти Решение: Так как при
Непрерывность функции в точке и на промежутке. Точки разрыва функции [4],§3; [3],гл.2,§9; [8],гл.6,§6; [9],гл.1,§5, [10]
Если функция у = f (х) определена в некоторой окрестности конечной точки а, то точка а называется точкой разрыва функции в двух случаях: 1) в точке х = а функция f (х) не определена; 2) в точке х = а функция f (х) определена, но не выполняется хотя бы одно из равенств:
где Если при этом Если хотя бы один из пределов в равенстве (3) не существует или бесконечный, то точка a называется точкой разрыва второго рода (точкой бесконечного разрыва, если хотя бы один из соответствующих пределов - бесконечный). Все элементарные функции непрерывны в каждой точке области определения. Пример 18. Найти точки разрыва функции у = f (x), определить тип разрыва. Для точек разрыва первого рода вычислить скачок функции. Построить график.
Решение: Внутри каждого из промежутков ( Найдем односторонние пределы в этих точках: 1. Для точки х = 0 имеем:
Оба односторонних предела конечны, но не равны между собой, значит, точка х = 0 есть точка разрыва I рода. В точке х = 0 функция f(x) имеет скачок 2. Рассмотрим точку х = 1.
Пример 19. Найти точки разрыва функции Решение: Преобразуем дробь:
Функция не определена в точках х = -1 и х = 3 и, следовательно, имеет в этих точках разрывы. Найдем соответствующие односторонние пределы: 1. Для точки х = -1 при
Аналогично вычислим
Так как оба предела конечны, то точка х = - 1 - точка разрыва первого рода. Поскольку пределы не равны, то это - конечный разрыв I рода.
Пример 20. Найти точки разрыва функции Решение: Даннаяэлементарная функция не определена в точках
При Производная и дифференциал [4],§4; [3],т.1,гл.3,§§2-16; [8],гл.7,§1; [9],гл.2,§§1-6
Вычисление производных Основные правила дифференцирования: Если функция и(х) и v(x) дифференцируемы в точке х, то в этой точке:
Таблица производных:
Пример 21. Найти производную функции Решение: Используем первое и второе правила дифференцирования
Далее используем формулу для нахождения производной степенной функции (табличная формула N 2):
Пример 22. Найти производную функции Решение: Используем правило дифференцирования произведения и табличные формулы N 4 и N 11:
Пример 23. Найти производную функции Решение: Используем правило дифференцирования частного и табличные формулы N 9 и N 13:
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 401; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.87.151 (0.006 с.) |

 бесконечно малые при
бесконечно малые при  называются эквивалентными, если
называются эквивалентными, если  . Эквивалентность бесконечно малых обозначается так:
. Эквивалентность бесконечно малых обозначается так:  ~
~  при
при  то
то ~
~  ~
~  ~
~  ~
~  ~
~  ;
;  ~
~  ;
; ~
~  ~
~  ;
;  ~
~ 
 то имеем неопределенность
то имеем неопределенность  Заменим исходные бесконечно малые эквивалентными
Заменим исходные бесконечно малые эквивалентными ~
~  ;
;  ~
~  ;
; 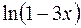 ~
~  ;
;  ~
~ 

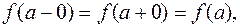 (3)
(3)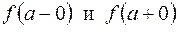 - левосторонний и правосторонний пределы функции
- левосторонний и правосторонний пределы функции  в точке а.
в точке а. ,то разрыв называется устранимым.
,то разрыв называется устранимым.
 ;0), (0; 1) и (1;
;0), (0; 1) и (1;  ) функция f(x) совпадает с соответствующей элементарной функцией. Следовательно, внутри каждого из этих промежутков функция f(x) будет непрерывной, и разрывы могут быть только на концах этих промежутков, то есть в точках x =0 и x =1.
) функция f(x) совпадает с соответствующей элементарной функцией. Следовательно, внутри каждого из этих промежутков функция f(x) будет непрерывной, и разрывы могут быть только на концах этих промежутков, то есть в точках x =0 и x =1.


 Односторонние пределы равны и совпадают со значением функции в рассматриваемой точке, значит, в этой точке функция f(x) непрерывна. График функции изображен на рис.9.
Односторонние пределы равны и совпадают со значением функции в рассматриваемой точке, значит, в этой точке функция f(x) непрерывна. График функции изображен на рис.9. ,установить тип разрыва, для точек разрыва первого рода вычислить скачок функции, построить график в окрестности точек разрыва.
,установить тип разрыва, для точек разрыва первого рода вычислить скачок функции, построить график в окрестности точек разрыва.
 и, значит,
и, значит,  Следовательно,
Следовательно,

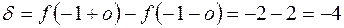 - скачок функции. В окрестности точки
- скачок функции. В окрестности точки 
 , поэтому
, поэтому  и, значит
и, значит

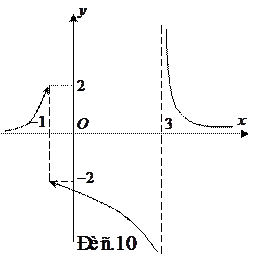 Таким образом, точка х = 3 - точка бесконечного разрыва второго рода. График функции представлен на рис.10.
Таким образом, точка х = 3 - точка бесконечного разрыва второго рода. График функции представлен на рис.10. , определить тип разрыва, начертить эскиз графика функции в окрестности точек разрыва.
, определить тип разрыва, начертить эскиз графика функции в окрестности точек разрыва. , следовательно, имеет в этой точке разрыв. Найдем односторонние пределы, учитывая, что
, следовательно, имеет в этой точке разрыв. Найдем односторонние пределы, учитывая, что  при
при  При
При  и
и 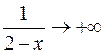 , следовательно,
, следовательно, 
 Таким образом, в точке
Таким образом, в точке  и
и  , следовательно,
, следовательно, 
 Заметим, что при
Заметим, что при  и
и  , т.е. прямая
, т.е. прямая  является горизонтальной асимптотой кривой. Эскиз графика функции изображен на рис.11.
является горизонтальной асимптотой кривой. Эскиз графика функции изображен на рис.11.