
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
К задачам аналитической геометрииСодержание книги
Поиск на нашем сайте
[2],гл.2,3; [8],гл.3,§1 Задачи на прямую и плоскость в пространстве рекомендуется решать средствами векторной алгебры. При решении задач необходимо уметь использовать различные формы уравнений прямых и плоскостей, а также уметь переходить от одной формы уравнения к другой. Пример 5. Составить уравнение плоскости, проходящей через точки Решение: Найдем координаты точки М3(х,у z) - точки пересечения заданной прямой с плоскостью хОу. Для этого от канонических уравнений прямой перейдем к параметрическим и, добавив уравнение плоскости хОу z = 0, получим систему для определения координат искомой точки:
Из третьего и четвертого уравнений получим t = 2, тогда x = 7; y = 2; z = 0. Таким образом, М 3(7,2,0) - точка пересечения заданной прямой с плоскостью хОу. Составим уравнение плоскости, проходящей через точки М1,М2,М3. Если точка М(х,у,z) - текущая точка плоскости, то векторы
Раскрыв этот определитель по элементам первой строки, получим уравнение искомой плоскости:
Пример 6. Найти уравнение плоскости, проходящей через точку Решение: Приведем общие уравнения прямой к каноническому виду
Т.о. уравнение искомой плоскости 11 х + у - 20 z - 1 = 0.
Геометрические образы уравнений на Плоскости и в пространстве [2],гл.4; [8], гл.3,§2; [10]
В декартовой системе координат на плоскости всякому уравнению первой степени относительно текущих координат соответствует прямая линия, а уравнению второй степени соответствует в общем случае кривая второго порядка - эллипс (окружность), гипербола или парабола. (Возможны и вырожденные случаи: например, уравнению Пример 7. Найти координаты точек пересечения кривых Решение: Определим вид кривых. Уравнение
Подставляя у2 = 5 - х из второго уравнения в первое, получим х2 - 7х + 6 = 0, откуда х1 = 1, x2 = 6. Тогда при В декартовой системе координат в пространстве всякому уравнению первой степени относительно текущих координат соответствует плоскость, а уравнению второй степени в общем случае соответствует поверхность второго порядка (за исключением вырожденных случаев). Пример 8. Тело в пространстве задано системой неравенств
Определить вид поверхностей, его ограничивающих, и изобразить это тело.
Решение: Уравнение х 2 + у 2 - (z - 2)2= 0 задает в пространстве конус с осью Oz, смещенный вдоль оси Oz на 2 (рис.3). Он разбивает все пространство на три части. Объединение двух из них, содержащих точки оси Oz, задается неравенством х 2 + у 2 - (z - 2)2 ≤ 0. Параболоид, задаваемый уравнением х 2 + у 2 = z (рис.4), разбивает пространство на две части, одна из которых и задается неравенством х 2 + у 2 ≤ z. Так как координаты точки A (0; 0; 2) удовлетворяют этому неравенству, то речь, очевидно, идет о части пространства, лежащей внутри параболоида. Наконец, z ≤ 2 задает то полупространство, которое лежит ниже плоскости z = 2. Поверхности х 2 + у 2 = z и х 2 + у 2- (z - 2)2 = 0 пересекаются в плоскости z = 1 по окружности х 2 + у 2 = 1. Объединяя эти результаты, мы получим, что исследуемое тело имеет вид, указанный на рис.5. Пример 9. Сделать схематический рисунок тела, заданного системой неравенств
Указать вид поверхностей, ограничивающих тело. Определить, по каким линиям и в каких плоскостях пересекаются эти поверхности.
Решение: Уравнение х 2 + у 2= 16 задает цилиндр с осью Oz, направляющей которого является окружность радиуса 4 с центром в начале координат (рис.6). Уравнение х 2 + у2 - z 2 = 12 задает однополостный гиперболоид (ось вращения - ось Oz), радиус "горла" (сечение плоскостью z = 0) равен На рис.8 изображено тело, ограниченное снаружи цилиндром, а изнутри однополостным гиперболоидом, которые пересекаются по двум окружностям с центрами на оси Oz, с одинаковыми радиусами R = 4, расположенными в плоскостях z = 2 и z = -2.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 610; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.212.225 (0.008 с.) |

 и точку пересечения прямой
и точку пересечения прямой  с плоскостью хОу.
с плоскостью хОу.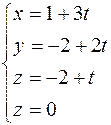
 и
и  - компланарны, следовательно, их смешанное произведение равно нулю:
- компланарны, следовательно, их смешанное произведение равно нулю:  или в координатной форме
или в координатной форме

 и прямую
и прямую 
 - направляющий вектор прямой, a
- направляющий вектор прямой, a  - точка, лежащая на этой прямой. Так как прямая лежит в обеих данных плоскостях, в плоскости х - у + 2 z + 1 = 0 и в плоскости Зх - у - z + 1 = 0, то ее направляющий вектор
- точка, лежащая на этой прямой. Так как прямая лежит в обеих данных плоскостях, в плоскости х - у + 2 z + 1 = 0 и в плоскости Зх - у - z + 1 = 0, то ее направляющий вектор  перпендикулярен нормальным векторам этих плоскостей N1 = (1; -1;2) и N2 = (3; -1; -1), поэтому можно выбрать
перпендикулярен нормальным векторам этих плоскостей N1 = (1; -1;2) и N2 = (3; -1; -1), поэтому можно выбрать
 Координаты точки
Координаты точки  . Выбирая одну из координат произвольно, например, положим
. Выбирая одну из координат произвольно, например, положим 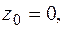 получим
получим  , откуда
, откуда  Значит,
Значит, 
 и канонические уравнения прямой имеют вид:
и канонические уравнения прямой имеют вид:  Теперь найдем уравнение плоскости, проходящей через прямую и точку А. Выберем произвольную точку искомой плоскости M(x,y,z), тогда три вектора
Теперь найдем уравнение плоскости, проходящей через прямую и точку А. Выберем произвольную точку искомой плоскости M(x,y,z), тогда три вектора 
 компланарны, (см.рис.1), значит
компланарны, (см.рис.1), значит 


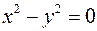 соответствуют две пересекающиеся прямые
соответствуют две пересекающиеся прямые  и
и  , а
, а  - точка
- точка  ,
,  ).
). и
и  Указать вид кривых. Сделать чертеж.
Указать вид кривых. Сделать чертеж. ;
; 
 определяет окружность с центром в точке (3; 0) и радиусом R = 2
определяет окружность с центром в точке (3; 0) и радиусом R = 2  .
.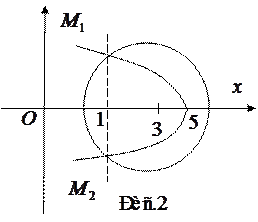 Уравнению х + у2 = 5 или у2 = -(x - 5) соответствует парабола, симметричная относительно оси 0х, ветви которой направлены влево, а вершина находится в точке (5,0). Координаты точек пересечения двух заданных линий являются решениями системы уравнений:
Уравнению х + у2 = 5 или у2 = -(x - 5) соответствует парабола, симметричная относительно оси 0х, ветви которой направлены влево, а вершина находится в точке (5,0). Координаты точек пересечения двух заданных линий являются решениями системы уравнений:
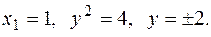 При х 2 = 6 уравнение у2 = 5 - х решения не имеет. Таким образом, заданные окружность и парабола пересекаются в двух точках
При х 2 = 6 уравнение у2 = 5 - х решения не имеет. Таким образом, заданные окружность и парабола пересекаются в двух точках 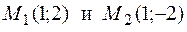 (см.рис.2).
(см.рис.2).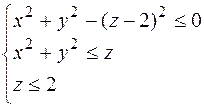



 (рис.7). Очевидно, что линиями пересечения поверхностей будут окружности того же радиуса, что и направляющая цилиндра. Определим, в каких плоскостях пересекаются поверхности. Для этого из уравнений системы исключим х и у: х 2+ у 2подставим в уравнение гиперболоида. Получим 16 - z 2 = 12 или z 2 - 4, откуда z = ±2.
(рис.7). Очевидно, что линиями пересечения поверхностей будут окружности того же радиуса, что и направляющая цилиндра. Определим, в каких плоскостях пересекаются поверхности. Для этого из уравнений системы исключим х и у: х 2+ у 2подставим в уравнение гиперболоида. Получим 16 - z 2 = 12 или z 2 - 4, откуда z = ±2.


