
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В задачах 71-80 найти первую производную функцииСодержание книги
Поиск на нашем сайте
В задачах 81-85 найти координаты точки пересечения с осью
В задачах 86-90 найти координаты точки пересечения с осью
В задачах 91-100 найти
Задание на контрольную работу № 3
В задачах 101-110 найти пределы, пользуясь правилом Лопиталя.
В задачах 111-120 исследовать функцию, построить ее график.
В задачах 121-130 найти неопределенные интегралы. Результат проверить дифференцированием.
В задачах 131-140 найти неопределенные интегралы, используя для вычислений формулу интегрирования по частям.
В задачах 141-150 вычислить определенные интегралы, используя подстановки, указанные в скобках:
Задание на контрольную работу № 4 В задачах 151-156 вычислить несобственный интеграл или доказать его расходимость.
В задачах 157-160 доказать, используя признак сравнения, сходится или расходится несобственный интеграл.
161. Найти площадь плоской фигуры, ограниченной линиями 162. Найти площадь плоской фигуры, ограниченной линиями 163. Вычислить площадь, заключенную внутри лемнискаты Бернулли 164. Определить длину дуги кривой: 165. Вычислить длину дуги астроиды 166. Вычислить площадь эллипса 167. Вычислить объем тела, образованный вращением вокруг оси Ох синусоиды 168. Вычислить площадь поверхности шарового пояса, получаемого при вращении вокруг оси Ох дуги окружности 169. Вычислить объем тела, образованный вращением вокруг оси Oy кривой 170. Найти длину дуги кривой В заданиях 171-174 для функции
В задачах 175-177 найти значение
В задачах 178-180 найти значение
В заданиях 181-185 найти в точке A полный дифференциал функции
В заданиях 186-190 найти в точке А полный дифференциал функции
В заданиях 191-200 найти наибольшее и наименьшее значения функции
Текущий контроль Тестовые задания
1. Вычислите определитель а) -1; б) 11; * в) 1; г) -11. 2. Алгебраическое дополнение а) 2; б) 1; в) -3; * г) -2. 3. Какое из утверждений верно для системы а) система имеет единственное решение, б) система несовместна, в) система имеет бесконечное множество решений. 4. При каком значении а) 5. Найти матрицу а) 6. Если а) в) 7. Вычислите длину вектора 1) 6 2) 25 3) 3 *4) 8. Укажите, какому из предложенных векторов коллинеарен вектор 1) 2 9. Записать уравнение сферы 1) 10. Записать уравнение конуса 1) 11. Напишите уравнение прямой, проходящей через точку М(2,0,4) и перпендикулярной плоскости 1) 3) 12. Составьте уравнение плоскости, проходящей через точку М(3,-1,4) и параллельной плоскости 1) 2) 13. Уравнение 1) параболу 2) гиперболу 3) эллипс 4) прямую 14. Определить вид поверхности 1) эллиптический параболоид 2) гиперболический цилиндр 3) однополостный гиперболоид 4) гиперболический параболоид 15. Указать вид кривой, полученной в пересечении гиперболического параболоида 1) парабола 2)эллипс 3)прямая 4) гипербола 16. Найдите область определения функции а) в) 17. Закончите фразу: последовательность а) ограничена сверху, но не ограничена снизу, б) ограничена снизу, но не ограничена сверху, в) ограничена, г) не ограничена ни снизу, ни сверху. 18. Вычислите а) 19. Вычислите а) 20. Определите, будет ли точка а) точка непрерывности, б) точка конечного разрыва, в) точка бесконечного разрыва, г) точка устранимого разрыва. 21. Дифференциал а) 22. Дифференциал а) 23. Найти произведение а) 24. Записать комплексное число а) 25. Вычислить 1) 3) 26. Вычислить 1) 27. Найти 1) 28. Вычислить 1) 29. Вычислить 1) 30. Значение функции а) 31. Частная производная а) 1; б) 3; в) 2; г) 32. Дифференциал функции а)
Содержание
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.28.173 (0.009 с.) |

 ,
,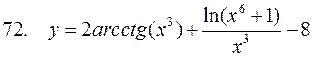 ,
,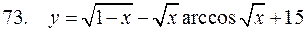 ,
,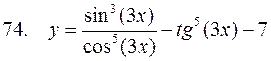 ,
, ,
, ,
, ,
, ,
,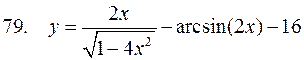 ,
, ,
, касательной, проведенной к графику функции
касательной, проведенной к графику функции 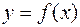 в заданной точке. Сделать чертеж.
в заданной точке. Сделать чертеж.
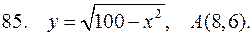
 касательной, проведенной к графику функции
касательной, проведенной к графику функции 
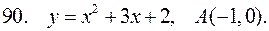
 и
и  функции, заданной параметрически
функции, заданной параметрически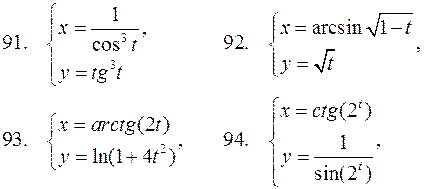


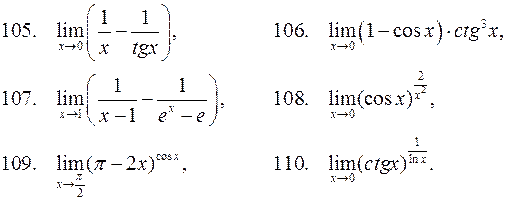
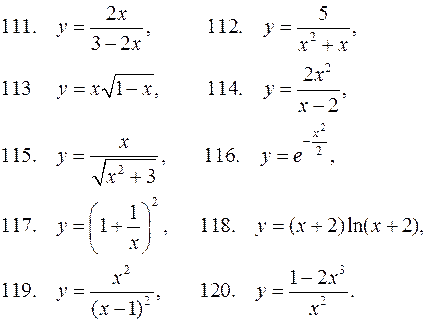


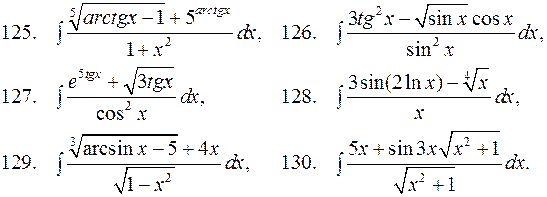
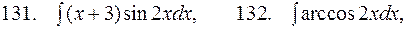


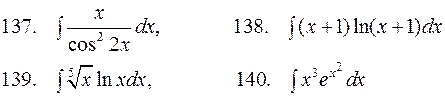




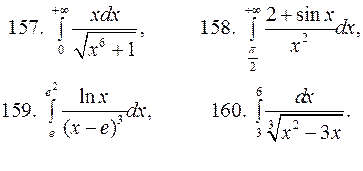
 и
и 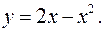 Сделать рисунок.
Сделать рисунок. Сделать рисунок.
Сделать рисунок. Построить эту кривую.
Построить эту кривую. Сделать рисунок.
Сделать рисунок. Сделать рисунок.
Сделать рисунок. Сделать рисунок.
Сделать рисунок.
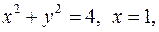
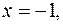
 Сделать рисунок.
Сделать рисунок. Сделать рисунок.
Сделать рисунок.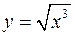 , от начала координат до точки В(4,8). Сделать рисунок.
, от начала координат до точки В(4,8). Сделать рисунок. убедиться, что
убедиться, что  .
.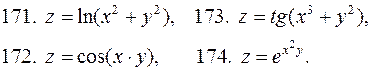
 в точке А.
в точке А.
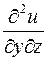 в точке А.
в точке А.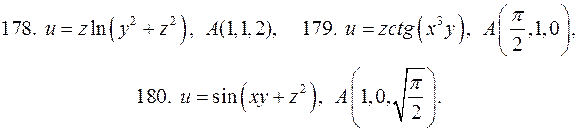
 , заданной неявно.
, заданной неявно.




 элемента
элемента 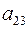 матрицы
матрицы 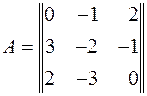 равно
равно ?
? система
система 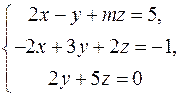 несовместна?
несовместна? б)
б) 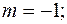 в)
в)  г)
г) 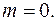
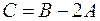 , если
, если 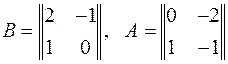 .
. ; * б)
; * б) 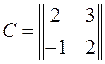 ; с)
; с)  ; г)
; г)  .
. , где
, где  - матрица третьего порядка, то ее определитель
- матрица третьего порядка, то ее определитель 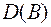 :
: ; б)
; б) 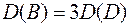 ;
; ; г)
; г)  .
. , если
, если 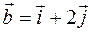 ,
,  .
.
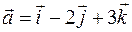 :
: 2)
2)  3)
3)  4)
4) 
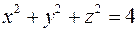 в сферической системе координат.
в сферической системе координат.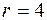 2)
2)  3)
3) 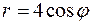 4)
4) 
 в цилиндрической системе координат.
в цилиндрической системе координат. 2)
2) 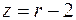 3)
3) 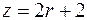 4)
4) 
 .
. 2)
2) 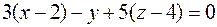
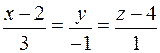 4)
4) 
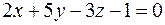 .
.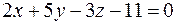 3)
3) 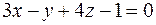
 4)
4) 
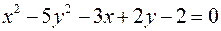 определяет на плоскости.
определяет на плоскости. :
: с плоскостью
с плоскостью  :
:
 ; б)
; б)  ;
; ; г)
; г) 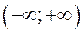 .
.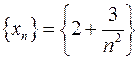

 , б)
, б)  , *в)
, *в)  , г)
, г) 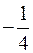 .
.
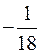 , б)
, б) 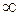 , *г)
, *г) 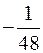 .
. точкой разрыва функции
точкой разрыва функции  , и если будет, то установите тип точки разрыва
, и если будет, то установите тип точки разрыва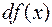 функции
функции  в точке
в точке  равен:
равен: ; б)
; б)  ; в)
; в) 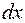 ; г)
; г)  .
. в точке
в точке  равен:
равен: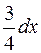 ; б)
; б)  ; г)
; г) 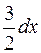 .
.
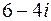 , б)
, б)  , в)
, в)  , г)
, г) 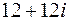 .
. в алгебраической форме
в алгебраической форме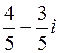 , б)
, б) 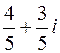 , в)
, в) 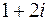 , г)
, г)  .
.
 2)
2) 


 2)
2) 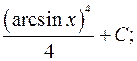 3)
3) 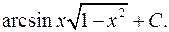

 2)
2)  3)
3) 

 2)
2) 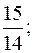 3)
3) 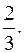
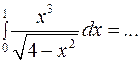
 2)
2)  3)
3) 
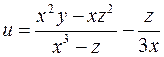 в точке
в точке 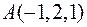 равно
равно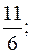 *б)
*б) 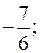 в)
в)  г)
г) 
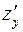 функции
функции  в точке
в точке  равна
равна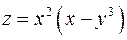 в точке
в точке 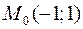 равен
равен б)
б)  в)
в)  г)
г) 



