
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несобственный интеграл от неограниченной функцииСодержание книги
Поиск на нашем сайте
Пусть функция f (х) непрерывна на промежутке[ а, b), а в точке b имеет бесконечный разрыв:
Несобственный интеграл называется сходящимся, если указанный предел существует и конечен, и расходящимся в противном случае. Аналогично определяется интеграл от функции, имеющей бесконечный разрыв на левом конце промежутка интегрирования. Пример 47. Вычислить несобственный интеграл Решение: Подынтегральная функция имеет бесконечный разрыв в точке 0, поэтому
Пример 48. Определить, сходится или расходится несобственный интеграл
Решение: Интеграл является несобственным, так как подынтегральная функция имеет бесконечный разрыв в точке х = 3 на всем промежутке интегрирования
Рассмотрим интеграл х = 5, t = 4. Тогда
Этот интеграл сходится. Следовательно, исходный интеграл сходится абсолютно и по теореме 1 - сходится. Геометрические приложения определенного интеграла [6],гл.2,§§7,8; [7],гл.2,§§7,8; [3],т.1,гл.12,§§1-6; [8],гл.10,§§3-6; [9],гл.5,§§7-10, [10]
Рассмотрим приложения определенного интеграла к вычислению площадей плоских фигур, объемов тел вращения и длин дуг кривых.
Вычисление площадей плоских фигур
Если фигура ограничена сверху графиком функции
Пример 49. Вычислить площадь круга радиуса R. Решение: Круг определяется неравенствами
Сделаем в этом интеграле замену
Пример 50. Вычислить площадь фигуры, заданной неравенствами:
Решение: Описанная фигура лежит под параболой и над биссектрисами 1-го и 2-го координатных углов (рис.18). Для вычисления ее площади разобьем промежуток интегрирования на два:
Пример 51. Вычислить площадь круга радиуса R, используя полярные координаты. Решение: В полярных координатах уравнение окружности радиуса R с центром в полюсе имеет вид
Решение: Вид фигуры, ограниченной данной кардиоидой, представлен на рис.20. Согласно условию, требуется найти площадь заштрихованной части фигуры, для которой полярный угол изменяется от 0 до
Вычисление длин дуг кривых
Если плоская дуга задана параметрическими уравнениями
и функции
Пример 53. Вычислить длину окружности радиуса R. Решение: Окружность радиуса R задается в параметрическом виде уравнениями
Если дуга задана в явном виде уравнением у = f(x), (а ≤x≤ b), то
Пример 54. Вычислить длину окружности радиуса R, используя формулу (4). Решение: Рассмотрим четверть окружности радиуса R с центром в начале координат, расположенную в первом координатном угле. Она задается уравнением
Этот интеграл является несобственным, так как подынтегральная функция имеет бесконечный разрыв на правом конце отрезка интегрирования. Вычислим его:
Если плоская дуга задана в полярных координатах уравнением
Пример 55. Вычислить длину окружности радиуса R, используя формулу (5). Решение: Окружность радиуса R с центром в полюсе системы координат задается уравнением
|
||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 567; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 . Несобственным интегралом
. Несобственным интегралом  от функции f (х) на промежутке[ а, b) называется предел
от функции f (х) на промежутке[ а, b) называется предел .
.

 .
.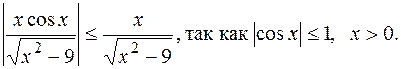
 . Сделаем в нем замену
. Сделаем в нем замену  , тогда
, тогда  и при х = 3, t = 0, а при
и при х = 3, t = 0, а при
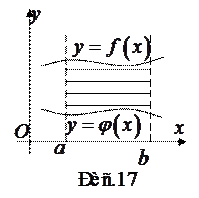
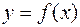 , a снизу графиком
, a снизу графиком  и прямыми
и прямыми  (рис.17), то ее площадь S находится по формуле
(рис.17), то ее площадь S находится по формуле
 . В таком случае
. В таком случае  , х изменяется от - R до R. Тогда
, х изменяется от - R до R. Тогда
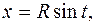 тогда
тогда 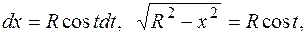 и при
и при 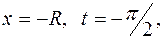 а при
а при  . Тогда
. Тогда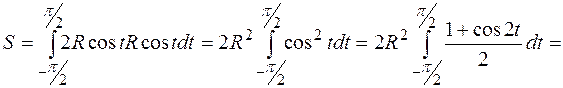
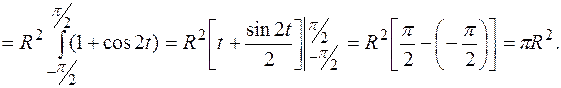


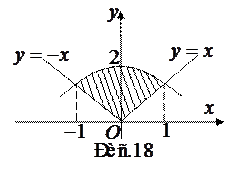 В полярной системе координат площадь сектора, ограниченного
В полярной системе координат площадь сектора, ограниченного 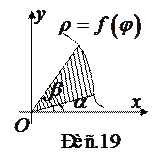 двумя лучами
двумя лучами 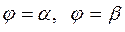 и кривой, заданной непрерывной функцией
и кривой, заданной непрерывной функцией 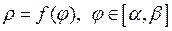 (рис.19), находится по формуле
(рис.19), находится по формуле
 Тогда для площади круга имеем
Тогда для площади круга имеем
 Пример 52. Найти площадь фигуры, ограниченной кардиоидой
Пример 52. Найти площадь фигуры, ограниченной кардиоидой 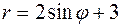 и лучами
и лучами 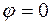 и
и 
 Тогда искомая площадь будет равна
Тогда искомая площадь будет равна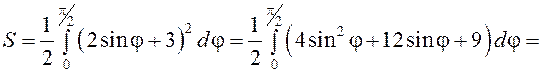

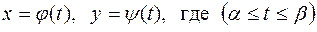 ,
, имеют непрерывные производные, не обращающиеся в ноль одновременно, то длина дуги
имеют непрерывные производные, не обращающиеся в ноль одновременно, то длина дуги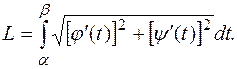
 тогда
тогда
 (4)
(4) Тогда
Тогда  и для длины окружности получаем
и для длины окружности получаем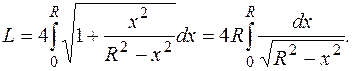
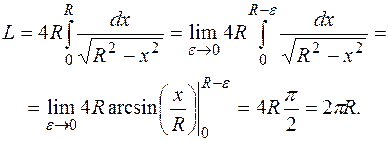
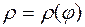 , где функция
, где функция  непрерывно дифференцируема на отрезке
непрерывно дифференцируема на отрезке  , а начальная и конечная точки дуги имеют полярные углы
, а начальная и конечная точки дуги имеют полярные углы  и
и 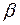 соответственно, то длина дуги вычисляется по формуле
соответственно, то длина дуги вычисляется по формуле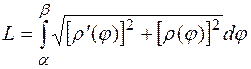 (5)
(5)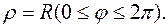 Тогда
Тогда  и длина
и длина



