
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференцирование функций, заданных параметрическиСодержание книги
Поиск на нашем сайте
Производная функции
Пример 27. Найти производные заданной в параметрической форме Решение: Вычислим
Используя формулу (2), получим
Итак,
Вычислим
Следовательно, используя формулу (3), получаем
Методические указания по выполнению контрольной работы N 3
Применение правила Лопиталя к нахождению Предела функции [5],гл.1,16; [3],т.1,гл.4,§§4-5; [8],гл.7,§2; [9],гл.11,§9, [10]
При отыскании предела 4.3.1. Раскрытие неопределенностей типа
Непосредственно применять правило Лопиталя можно только для раскрытия неопределенностей типа
если выполнены условия: 1) функции f(x), g(x) дифференцируемы в некоторой окрестности точки х = а и g'(х) ≠ 0 в этой окрестности (кроме, может быть самой точки а); 2) 3) существует Пример 28. Найти Решение: Поскольку
Так как этот предел существует, то согласно правилу Лопиталя:
Замечание. Если предел отношения производных
4.3.2. Раскрытие неопределенностей типа
Неопределенность типа Пример 29. Найти Решение: При
Получена неопределенность типа
(поскольку
Пример 30. Найти Решение: Выражение в скобках, представляющее собой неопределенность типа
Полученную неопределенность типа
4.3.3. Раскрытие неопределенностей типа
При раскрытии указанных неопределенностей используются: а) основное логарифмическое тождество б) непрерывность показательной функции, в силу чего:
Пример 31. Найти Решение: Поскольку
Теперь используем основное логарифмическое тождество и свойство непрерывности показательной функции:
Таким образом, для вычисления
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.201.46 (0.007 с.) |

 , заданной в параметрической форме:
, заданной в параметрической форме: 
 , находится по формуле
, находится по формуле (2)
(2) и
и  функции
функции 

 и
и 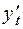 :
: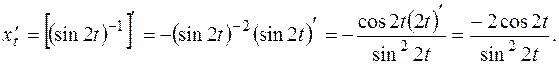
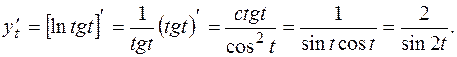

 Так как
Так как  , то для нахождения
, то для нахождения  (3)
(3) :
:

 подстановка предельного значения
подстановка предельного значения  в ряде случаев приводит к неопределенным выражениям типа:
в ряде случаев приводит к неопределенным выражениям типа:  . Тогда вычисление заданного предела называют раскрытием неопределенности соответствующего типа. Обычно при этом используют правило Лопиталя.
. Тогда вычисление заданного предела называют раскрытием неопределенности соответствующего типа. Обычно при этом используют правило Лопиталя. и
и 


 (конечный или бесконечный), при этом а может быть как числом, так и одним из символов:
(конечный или бесконечный), при этом а может быть как числом, так и одним из символов: 


 и
и  то имеем неопределенность типа
то имеем неопределенность типа  дифференцируемы на всей числовой оси. Найдем предел отношения их производных:
дифференцируемы на всей числовой оси. Найдем предел отношения их производных: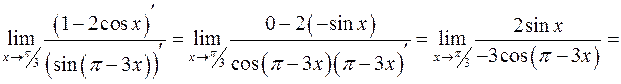


 и
и 

 аргумент логарифмической функции
аргумент логарифмической функции  Так как
Так как  и
и  , то возникает неопределенность типа
, то возникает неопределенность типа 

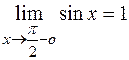 ). Здесь имеет место неопределенность типа
). Здесь имеет место неопределенность типа 





 (в частности,
(в частности,  );
);
 .
.
 , имеем неопределенность типа
, имеем неопределенность типа  . Найдем вначале предел логарифма заданной функции:
. Найдем вначале предел логарифма заданной функции:  . Здесь возникла неопределенность типа
. Здесь возникла неопределенность типа  , то перейдем к неопределенности типа
, то перейдем к неопределенности типа 


 в случае неопределенностей
в случае неопределенностей 
 .
.


