
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление площадей поверхностей вращенияСодержание книги
Поиск на нашем сайте
Если плоская дуга АВ задана уравнением
Пример 56. Вычислить площадь сферы радиуса R. Решение: Сфера радиуса R может быть получена вращением полуокружности
Вычисление объемов тел вращения
Если плоская дуга АВ задана уравнением
Если плоская дуга CD задана уравнением
Пример 57. Вычислить объем шара радиуса R. Решение: Шар радиуса R может быть получен вращением полукруга
Дифференциальное исчисление функции Нескольких переменных
Переменная z называется функцией независимых переменных х, у в множестве Е, если каждой паре (х,у) значений этих переменных из Е ставится в соответствие одно определенное значение z. Аналогично определяются и функции большего числа переменных. Частные производные [6],гл.З; [7],гл.3,§§4,5,7,8; [3],т.1,гл.8,§§5,7,10,12; [8],гл.8,§2; [9],гл.6,§§3,4,7,9, [10]
Для функции нескольких переменных вводится понятие частной производной по каждому из аргументов. Если z = f(x,y), то по определению Аналогично определяется и частная производная по y
При вычислении частных производных все аргументы функции, за исключением той, по которой производится дифференцирование, считаются постоянными (константами). При вычислении частных производных применяются те же приемы, что и при вычислении обыкновенных производных. Пример 58. Вычислить z'x и z'y для функции Решение: Найдем z'x. Считаем у2 величиной постоянной, выносим его за знак производной. Дифференцируем xsinx no x как произведение.
Для
Частные производные второго порядка - это частные производные от производных первого порядка. Например:
Если функция Пример 59. Вычислить Решение: По определению частных производных высших порядков, можно найти искомую производную следующим образом:
где Пример 60. Вычислить у'х и дифференциал dy, если Решение: В данном случае
Если функция z от х, у задана неявно уравнением типа F(x, у, z) = 0, то частные производные z по х, у могут быть вычислены из соотношений
Полный дифференциал Если функция
Пример 61. Найти полный дифференциал dz в точке Решение: Поскольку функция z (x, у)задана неявно, то ее частные производные z'x, z'y можно найти, используя соотношения (6), где
В точке
|
||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 593; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 , причем f(x) неотрицательна и имеет непрерывную производную на (а,b), то площадь поверхности, полученной при вращении дуги АВ вокруг оси Ох может быть вычислена по формуле
, причем f(x) неотрицательна и имеет непрерывную производную на (а,b), то площадь поверхности, полученной при вращении дуги АВ вокруг оси Ох может быть вычислена по формуле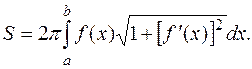
 , вокруг оси Ох. Тогда
, вокруг оси Ох. Тогда  и для площади поверхности сферы получаем
и для площади поверхности сферы получаем
 .
. , причем
, причем  неотрицательна, то объем тела, полученного при вращении криволинейной трапеции, расположенной под дугой CD, вокруг оси Оу может быть вычислена по формуле
неотрицательна, то объем тела, полученного при вращении криволинейной трапеции, расположенной под дугой CD, вокруг оси Оу может быть вычислена по формуле
 , вокруг оси Ох. Тогда для объема шара имеем
, вокруг оси Ох. Тогда для объема шара имеем
 частная производная z по х в точке
частная производная z по х в точке  .
. .
. .
.
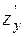 получаем
получаем

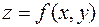 обладает в некоторой точке непрерывными частными производными z"xy и z"yx, то эти производные равны. Аналогичный факт справедлив и для производных более высоких порядков и для большего числа аргументов, что позволяет выбирать порядок дифференцирования.
обладает в некоторой точке непрерывными частными производными z"xy и z"yx, то эти производные равны. Аналогичный факт справедлив и для производных более высоких порядков и для большего числа аргументов, что позволяет выбирать порядок дифференцирования.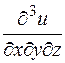 для функции
для функции  .
.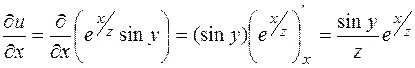

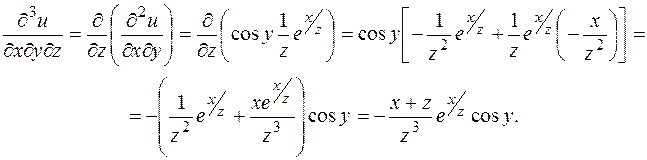 Если функция у от х задана неявно уравнением типа
Если функция у от х задана неявно уравнением типа  , то производная у по х вычисляется по формуле:
, то производная у по х вычисляется по формуле: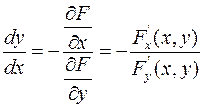 .
. - частные производные от F(x,y) по х,у соответственно.
- частные производные от F(x,y) по х,у соответственно.
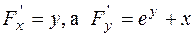 . Тогда
. Тогда
 (6)
(6)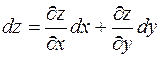
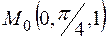 для функции z (x, у),заданной уравнением
для функции z (x, у),заданной уравнением 
 Тогда
Тогда
 Следовательно, в этой точке
Следовательно, в этой точке  и полный дифференциал
и полный дифференциал



