
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функции. Последовательности. Пределы.Содержание книги
Поиск на нашем сайте
Необходимо хорошо усвоить теоремы о пределах:
Приступим к отысканию пределов функций. Вопрос о пределе функции не имеет смысла, если не указан предел аргумента. Рассмотрим решение примеров.
Пример 1. Вычислить.
Решение. Применяя теоремы 1, 2, 3, 5, запишем
Пример 2. Вычислить
Пример 3. Вычислить
Решение
Пример 4. Вычислить
множители и сократим дробь на (х -I):
Допредельное значение х-1=0, поэтому сокращение на (х -1) законно.
Пример 5. Вычислить
Решение. Разделим числитель, и знаменатель дроби на х4:
Пример 6. Вычислить
Решение. Заменим sin Зх эквивалентной бесконечно малой Зх:
Пример 7. Вычислить
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ 1. Дайте определение функции. 2. Перечислите способы задания функции. Приведите примеры. 3. Сформулируйте определение числовой последовательности. 4. Какие бывают числовые последовательности? 5. Сформулируйте теорему о существовании предела последовательности. 6. Какая существует зависимость, между бесконечной малой и бесконечно большой последовательностями?
7. Дайте определение предела переменной. 8. Напишите уравнение гармонического колебания. 9. Как определяются функции y==arcsin х, y=arccos x, у= =arctg x, у=arcctg х? 10. Чему равно выражение y=sin(arcsin x)? 11. Как найти приращение аргумента? 12. Как найти приращение функции? 13. Как вычисляется средняя скорость изменения функции? 14. Дайте определение производной функции. 15. Выпишите теоремы о производных алгебраической суммы, произведения, частного.
Неопределенный интеграл
Понятие неопределенного интеграла. дифференцирование -это действие, с помощью которого по данной функции находится ее производная или дифференциал. Например, если F(x) = х10, то F' (х) = 10х9, dF (х) =10x9dx. Интегрирование -это действие, обратное дифференцированию. С помощью интегрирования по данной производной или дифференциалу функции находится сама функция. Например, если F' (х) = 7х6, то F (х) == х7, так как (х7)'=7х6. Дифференцируемая функция F(x), хЄ]a; b[ называется первообразной для функции f (х) на интервале ]а; Ь[, если F' (х) = f (х) для каждого хЄ]a; b[. Так, для функции f(x) = 1/cos3 х первообразной служит функция F(x)= tg x, поскольку (tg x)'= 1/cos2 х.
Например, 5x4dx = х5 + С, так как (х3 + С)' = 5х4. Приведем основные свойства неопределенного интеграла. 1.Дифференциал неопределенного интеграла равен подынтегральному выражению:
2.Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной, т. е.
аf(х)dx = a f(x)dx 4. Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов от каждой функции:
Основные формулы интегрирования
1.
2.
3.
4.
5.
7.
8.
9.
10.
11.
Если интеграл затруднительно привести к табличному с помощью элементарных преобразований, то в этом случае пользуются методом подстановки.
Пример 1. Найти
Решение. Произведем подстановку 2 — Зх2 = t тогда -6xdx =dt, xdx = -(1/6)dt. Далее, получаем
Пример 2. Найти Решение. Сначала положим 2 + cos x = t; тогда -sin xdx= dt, откуда sin xdx = -dt. Далее, получаем
Пример 3. Найти Решение. Положим 10х = t; тогда 10dx = dt, откуда dx=(1/10)dt. Далее, получаем
В практике интегрирования часто встречаются интегралы, для нахождения которых можно использовать следующие формулы (k = 0, n= 0 — постоянные):
1.
2.
4.
5.
6.
7.
8.
Вопросы и упражнения для самопроверки 1. Какое действие называется интегрированием? 2. Какая функция называется первообразной для функции f(x)? 3. Дайте определение неопределенного интеграла. 4. Перечислите основные свойства неопределенного интеграла. 5. Каким действием можно проверить интегрирование?
7. Найдите интегралы: а) б) в)
г)
Ответы: 7. а) б) в)
г) Определенный интеграл
Понятие определенного интеграла. Непосредственное вычисление определенного интеграла производится по формуле Ньютона—Лейбница:
где а—нижний предел, Ь—верхний предел, F (x)—какая-нибудь первообразная функции f (х).
Пример 1. Вычислить интеграл
Решение. Воспользуемся определением степени с дробным и отрицательным показателем и вычислим определенный интеграл:
Приведем основные свойства определенного интеграла. 1. При перестановке пределов интеграла знак интеграла меняется на противоположный:
4. Интеграл от суммы функций равен сумме интегралов от всех слагаемых:
Решение. 1) Произведем подстановку х3+2=t; тогда
3х2dx=dt, 2) Определим пределы интегрирования для переменной t. При х=1 получаем tн=13+2=3, при х=2 получаем tв=23+2=10. 3) Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим
Пример 3. Вычислить интеграл Решение. 1) положим cos х=t; тогда – sinxdx =dt и sinxdx = -dt. 2) Определим пределы интегрирования для переменной t: tн=cos0=1:tв=cos (π/2)=0. 3) Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим
Пример 4. Вычислить интеграл
Решение. Сначала преобразуем подынтегральное выражение sin3x = sin2 x • sin x = (1 — cos2x) sin x = sin x - cos2 x sin x. Затем вычислим интеграл от разности функций, заменив его разностью определенных интегралов от каждой функции:
Вычислим каждый интеграл отдельно:
Тогда
Приложения определенного интеграла. Площадь плоской фигуры. Площадь криволинейной трапеции аАВЬ (рис. 46), ограниченной гpaфикoм непрерывной функции y=f(x), где хЄ[а, b], отрезком [a,b] оси Ох, отрезками прямых х =a и х = b, вычисляется по формуле
(1) Пример 5. Вычислить площадь фигуры, ограниченной параболой у = х2 , прямыми х = - 1, х = 2 и осью абсцисс (рис.47). Решение. Применяя формулу (1), получаем
т.е. S=3 кв. ед. Площадь фигуры ABCD (рис. 48), ограниченной графиками непрерывных функций у =f1(x) и у f2= (x), где х Є[а, b], отрезками прямых х = а и х = Ь, вычисляется по формуле
(2)
Пример 6. Вычислить площадь фигуры, ограниченной осью Ох и линией у = х2 — 2х (рис. 49). Решение. Найдем пределы интегрирования, т. е. абсциссы точек пересечения графиков функций y=х2—2х и у=0 (ось Ох). Для этого решим систему
Теперь найдем искомую площадь:
Пример 7. Вычислить площадь фигуры, ограниченной линиями у = х2 и у2 =х (рис. 50). Решение. Найдем пределы интегрирования, т. е. абсциссы точек пересечения графиков функций у = х2 и у2 =х. Для этого решим систему
Искомую площадь вычисляем по формуле (2) при f1(x)=x2,
Объем тела вращения. Объем тела, образованного вращением вокруг оси Ох криволинейной трапеции аАВЬ, ограниченной непрерывной кривой у = f (x), где x Є [а, b], отрезком [а, Ь] оси Ох, отрезками прямых х = а и х = b (рис. 51), вычисляется по формуле
Пример 8. Вычислить объем тела, образованного вращением вокруг ocи Ох фигуры, ограниченной параболой у2=2х, прямой х = 3 и осью Ох (рис. 52). Решение. Применяя формулу (3), находим искомый объем:
(куб. ед.)
Объем тела, образованного вращением вокруг оси Оу криволинейной трапеции аАВЬ, ограниченной непрерывной кривой x=f(y), где у Є [а, b], отрезком [а, b] оси Оу, отрезками прямых у = а и у = Ь (рис. 53), вычисляется по формуле
(4)
Пример 9. Вычислить объем тела, образованного вращением вокруг ocи Оу фигуры, ограниченной параболой у=х2 и прямой у = 4 (рис. 54). Решение. Применяя формулу (4), находим искомый объем:
(куб. ед.)
Путь, пройденный точкой. Если точка движется прямолинейно и ее скорость v=f(t) есть известная функция времени t, то путь пройденный точкой за промежуток времени [t1,t2], вычисляется по формуле
(5) Вопросы для самопроверки
1. Дайте определение определенного интеграла. 2. Перечислите основные свойства определенного интеграла. 3. В чем заключается геометрический смысл определенного интеграла? 4. Напишите формулы для определения площади плоской фигуры с помощью определенного интеграла. 5. По каким формулам находится объем тела вращения? 6. Напишите формулу для вычисления пути, пройденного телом. 7. Напишите формулу для вычисления работы переменной силы. 8. По какой формуле вычисляется сила давления жидкости на пластинку?
Производная и ее приложения Производная. Понятие производной является одним из важнейших в курсе математики. Многие задачи как самой математики, так и естествознания и техники приводят к этому понятию.
Функция, имеющая конечную производную, называется дифференцируемой. Операция нахождения производной называется дифференцированием. Если у=f(u) и u=φ(x)— дифференцируемые функции своих аргументов, то производная сложной функции у=f(φ(x)) существует и равна произведению производной функции у по промежуточному аргументу u на производную промежуточного аргумента u по независимой переменной х:
Аналогичная формула верна и для сложных функций, которые задаются с помощью цепочки, содержащей три звена и более. Таблица формул дифференцирования 1. с’=0 2. х’=1 3. (u±v)’ = u’ ± v’ 4. (uv)’ = uv’ + vu’ 5. (cu)’ = cu’ 6. 7. 8. 9. 10. (au)’ = au ln a • u’ 11. (eu)’ = eu ln eu’ = euu’ 12. 13. 14. (sin u)’ = cos u • u’ 15. (cos u)’ = - sin u • u’ 16. 17. 18. 19. 20.
21. Здесь u и v — дифференцируемые функции от х, а с - постоянная величина. Пример 1. Найти производную функции Решение. Дифференцируем функцию по формулам
Пример 2. Найти производную функции у=sin3j и вычислить ее значение при j= p/3. Решение. Это сложная функция с промежуточным аргументом sinj. Дифференцируем ее по формулам (un)' = nun-1u', (sin u)' = cos u • u': f(j) = 3 sin2j (sinj)' = 3 sin2j cosj.
Вычислим значение производной при j = p/З: f(p/3) = 3sin2 (p/3) cos(p/3)=3(Ö3/2)2 •(1/2)=3•(3/4) • (1/2)=9/8. Пример 3. Найти производную функции
Решение. Сначала преобразуем функцию, используя свойства логарифмов: t
Дифференцируя, получим
Геометрический смысл производной. Производная функции у =f(x) представляет собой угловой коэффициент касательной, проведенной к графику функции в любой его точке. Угловой коэффициент касательной, проведенной к графику функции y=f(х) в точке A(а;b), равен значению производной функции при х = а: kкас=y'(a)=f'(a). Уравнение касательной, проведенной к графику функции в этой точке, имеет вид у— b=k (х -а), где k=f’(a). Пример 4. Составить уравнение касательной, проведенной к графику функции Решение. Сначала найдем ординату точки касания А (2;у). Так как точка А лежит на кривой, то ее координаты удовлетворяют уравнению кривой, т. е.
Уравнение касательной, проведенной к кривой в точке А(2;2), имеет вид у - 2 = k(x - 2). Для нахождения углового коэффициента касательной найдем производную:
Угловой коэффициент касательной равен значению производной функции при х = 2:
Уравнение касательной таково: у - 2 = - (х - 2), или у - 2 = -х + 2, т. е. х + у - 4 = 0.
Физический смысл производной. Если тело движется по прямой по закону s = s (t), то производная пути s по времени t равна скорости движения тела в данный момент времени t:
Быстрота протекания физических, химических и других процессов также выражается с помощью производной. Производная функции у=f(х) равна скорости изменения этой функции при данном значении аргумента х:
Пример 5. Закон движения точки по прямой задан формулой s=t2+3t+5. В какие моменты времени t скорость движения точки равна нулю? Решение. Скорость прямолинейного движения точки равна производной пути s по времени t: v (t) = s' = 3 t2 - 6t + 3; v (t) =0,З t2 - 6t + 3 = 0, t2 - 2t + 1 = 0, (t — 1)2 = 0, откуда t = 1. Вторая производная. Производной второго порядка (или второй производной) функции называется производная от первой производной у' =f' (х): у" = (у’)' или f" (х) = (f' (х))'. Пример 6. Найти вторую производную функции f(x)=tg x. Решение. Сначала по формуле Дифференцируя еще раз по формулам
Физический смысл второй производной. Если тело движется прямолинейно по закону s=s(t), то вторая производная пути s по времени t равна ускорению движения тела в данный момент времени t: а (t) = v' = s". Пример 7. Точка движется по прямой по закону s=t3-5t2+8t+2. (s - в метрах, t - в секундах). Найти ускорение движения точки в конце второй секунды. Решение. Сначала найдем производную пути s по времени t: s' = 3 t2 - 10 t + 8. Ускорение прямолинейного движения точки равно второй производной пути s по времени t: а (t) = s" = 6 t - 10, а(2) = 6 • 2 - 10 = 12 - 10 = 2. Ускорение движения точки в конце второй секунды равно 2 м/с2.
Приложения производной к исследованию функций. Дифференцируемая функция у= f (х) возрастает на промежутке ]а, b[, если ее производная положительна в каждой точке этого промежутка. Дифференцируемая функция у=f(x) убывает на промежутке]а; b[, если ее производная отрицательна в каждой точке этого промежутка. Функция y=f(x) имеет максимум в точке х = x1 (рис. 38), если для всех значений х, достаточно близких к x1, выполняется неравенство f(х) < f(х1); x=х1 - точка максимума; уmaх =f (х1) - максимум функции. Функция у = f(x) имеет минимум в точке х = х2 (рис. 38), если для всех значений х, достаточно близких к х2, выполняется неравенство f(x) > f(х2); х = х2 - точка минимума; уmaх = f(х2) - минимум функции. Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - экстремальными. Точки, в которых производная функции обращается в нуль, называются критическими, точками I рода. Первое достаточное условие существования экстремума функции. Если при переходе через критическую точку I рода х=х0 производная функции y=f(х) меняет знак, то х=х0 - точка
экстремума. При этом если производная меняет знак с плюса на минус, то х=х0= - точка максимума, а уmах =f(х0). Если же производная меняет знак с минуса на плюс, то х= х0 - точка минимума, a уmin =f(х0) Второе достаточное условие существования экстремума функции. Если в точке х = х0 первая производная функции у=f(x) обращается в нуль, а вторая производная отлична от нуля, то х=х0 - точка экстремума. При этом если вторая производная в этой точке положительна (f" (х0)>0), то х=х0 - точка минимума; если вторая производная в этой точке отрицательна (f"(х0) < 0), то х= х0 – точка максимума. рис. 38.
Направление вогнутости и точки перегиба кривой. Говорят, что на промежутке ]а, b[ кривая обращена выпуклостью вверх или выпукла (Ç), если она лежит ниже касательной, проведенной в любой ее точке (рис. 42). Говорят, что кривая на промежутке ]b,с[ обращена выпуклостью вниз или вогнута (È), если она лежит выше касательной, проведенной в любой ее точке (рис. 42). Точка А, в которой меняется направление вогнутости кривой, называется точкой перегиба кривой (рис. 42). График дифференцируемой функции y=f(x) является выпуклым на промежутке ]а; b[, если вторая производная функции отрицательна в каждой точке этого промежутка. График дифференцируемой функции y=f(x) является вогнутым на промежутке ]b; с[, если вторая производная функции положительна в каждой точке этого промежутка. Точки, в которых вторая производная функции обращается в нуль, называются критическими точками II рода. Если при переходе через критическую точку II рода х = х0 вторая производная функция меняет знак, то х = х0 - абсцисса точки перегиба. Ордината точки перегиба равна значению
функции в точке х0, т.е. ут.п. =f(х0); А(х0;f(х0)) - точка перегиба графика функции у = f(х). Исследование функций и построение их графиков. Исследование функции можно проводить по следующей схеме: 1. Найти область определения функции. 2. Найти точки пересечения графика функции с осями координат. 3. Найти промежутки монотонности и экстремумы функции. 4. Найти направление вогнутости и точки перегиба графика функции. 5. Для уточнения графика функции рекомендуется найти несколько дополнительных точек из уравнения функции. Пример 8. Построить график функции у = х3 - Зх. Решение 1. Областью определения функции служит множество всех действительных чисел, т. е. х = R. 2. Находим точки пересечения графика функции с осями координат:
3. Находим экстремумы функции. Для этого сначала найдем производную у' = Зх2 - 3. Затем найдем критические точки I рода: у' = 0,Зх2 - 3=0, х2 = 1, х1= 1, х2 = -1. Отметим эти точки на числовой прямой (рис. 43). Исследуем знак производной в каждом интервале; у'(-2) > 0, у' (0) < 0, у'(2) > 0. Функция возрастает при хÎ] -¥,-1[U]1,+¥[и убывает при хÎ] –1,1[. Итак, х= -1 — точка максимума; уmaх = у(-1)=(-1)3-3(-1)=-1+3=2; х=1 — точка минимума; ymin = у (1) = 13—3*1=1-3=-2.
4. Находим направление вогнутости и точки перегиба графика функции. Для этого сначала найдем вторую производную у" = 6х, а затем критические точки II рода: у" =0,6х=0, х = 0. Отметим эту точку на числовой прямой (рис. 44). Исследуем знак второй производной в каждом интервале: у"(-1) < 0, у"(1)>0.
Таким образом, график является выпуклым при хÎ] -¥,0[ и вогнутым при хÎ] 0, + ¥ [; х = 0 — абсцисса точки перегиба, yт.п= у(0) = 0; О (0,0) - точка перегиба графика функции. Отметим все полученные точки в системе координат и соединим их плавной кривой (рис. 45). Для уточнения графика функции можно найти дополнительные точки, используя уравнение функции: у(-2)= -2, у (2) =2.
Вопросы для самопроверки 1. Дайте определение производной функции. 2. В чем состоит геометрический смысл производной? 3. В чем состоит физический смысл производной? 4. Дайте определение второй производной функции. 5. В чем состоит физический смысл второй производной? 6. Напишите все формулы дифференцирования. 7. Как найти промежутки возрастания и убывания функции? 8. Как найти точки экстремума и экстремумы функции? 9. Как найти промежутки выпуклости и вогнутости кривой? 10. Как найти точки перегиба кривой?
11. Найдите производные функций: а) у = In tg (х/2); б) у = cos2 Öx; в) f(x)=(x+1)2х-1. 12. Составьте уравнение касательной к кривой у = х2 — 4х в точке с абсциссой х = 1. 13. Прямолинейное движение точки задано уравнением
(s - в метрах, t - в секундах). Найдите скорость и ускорение движения точки в конце второй секунды, 14. Какой из прямоугольников с периметром, равным 48см, имеет наибольшую площадь? 15. Число 66 представьте в виде суммы двух положительных слагаемых так, чтобы произведение этих чисел было наибольшим.
Ответы. 11. a) cosec х; б) 12. 2х+у+1=0. 13. 3 м/с, 2 м/с2. 14. Квадрат со стороной 12 см. 15. 33 и 33.
Решение. Находим производную данной функции, используя формулы
Умножив производную на дифференциал аргумента, получим дифференциал: Пример 2. Вычислить значение дифференциала функции n = In sin 2j при j = p/8, Dj = 0,02. Решение: Дифференциал функции вычисляем по формуле dv = v' (j) dj.
Прежде чем применить эту формулу, используя равенства
Понятие о дифференциальном уравнении. Дифференциальным уравнением называется уравнение, связывающее независимую переменную, искомую функцию, ее производную (или дифференциал аргумента и дифференциал функции). Если дифференциальное уравнение содержит производную или дифференциал не выше первого порядка, то оно называется дифференциальным уравнением первого порядка. Общий вид такого уравнения F (х, у, у') = 0. Общим решением дифференциального уравнения первого порядка называется функция у = j(х, С) от х и произвольной постоянной С, обращающая это уравнение в тождество. Общее решение, записанное в неявном виде Ф (х, у. С) =0, называется общим интегралом. Частным решением уравнения F (х, у, у') = 0 называется решение, полученное из общего решения при фиксированном значении С: у =j(х, Со), где Со - фиксированное число. Частным интегралом уравнения F(x, у, у') = 0 называется интеграл, полученный из общего интеграла при фиксированном значении С: Ф (х, у, Со) = 0. График любого частного решения дифференциального уравнения F (х, у, у') = 0 называется интеграл |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.49.213 (0.013 с.) |





 Решение
Решение
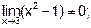


 Решение. В данном случае теорема о пределе частного не применима, так как Числитель дроби разложим на
Решение. В данном случае теорема о пределе частного не применима, так как Числитель дроби разложим на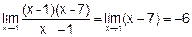





 Решение.
Решение. Совокупность всех первообразных функций f(x) на интервале ]а; b[ называют неопределенным интегралом от функции f(x) на этом интервале и пишут f (x)dx = F(x) + С. Здесь f(x)dx - подынтегральное выражение;
Совокупность всех первообразных функций f(x) на интервале ]а; b[ называют неопределенным интегралом от функции f(x) на этом интервале и пишут f (x)dx = F(x) + С. Здесь f(x)dx - подынтегральное выражение; (табличные интегралы).
(табличные интегралы).




 6.
6.















 3.
3.





 6. Напишите основные формулы интегрирования (табличные интегралы).
6. Напишите основные формулы интегрирования (табличные интегралы).





 Из этой формулы виден порядок вычисления определенного интеграл 1) находят одну из первообразных F (x) данной функции; 2) находят значение F (x) при х = а и х = Ь; 3) вычисляют разность F (Ь) — F (а).
Из этой формулы виден порядок вычисления определенного интеграл 1) находят одну из первообразных F (x) данной функции; 2) находят значение F (x) при х = а и х = Ь; 3) вычисляют разность F (Ь) — F (а).

 2. Отрезок интегрирования можно разбивать на части:
2. Отрезок интегрирования можно разбивать на части: 3. Постоянный множитель можно выносить за знак интеграла:
3. Постоянный множитель можно выносить за знак интеграла:
 Пример 2. Вычислить интеграл
Пример 2. Вычислить интеграл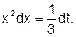






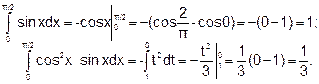














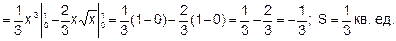


 (3)
(3)



 Производной функции y=f(x) в точке х называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:
Производной функции y=f(x) в точке х называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:

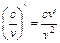


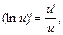 где u>0
где u>0 где u>0
где u>0











 в точке с абсциссой х=2.
в точке с абсциссой х=2.




 найдем первую производную:
найдем первую производную: 
 (un)’=nun-1u’, сos u)’=-sin u*u’, найдем вторую производную:
(un)’=nun-1u’, сos u)’=-sin u*u’, найдем вторую производную:










 в)
в) 


 (sin u)’ = cos u , u ’, (си)’= си ’, находим производную функции и ее значение при j = p/8:
(sin u)’ = cos u , u ’, (си)’= си ’, находим производную функции и ее значение при j = p/8:



