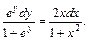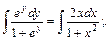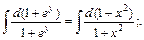Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общий интеграл этого уравнения имеет видСодержание книги
Поиск на нашем сайте
Замечание. Если произведение X1(x)•Y(у)=0 при х = а и у=b, то эти функции х=а и у=b являются решениями дифференциального уравнения при условии, что при этих значениях х и у уравнение не теряет числового смысла. Геометрически эти решения представляют собой прямые,
параллельные осям координат. Пример 2. Решить уравнение Решение. Так как
Интегрируя, находим
После потенцирования получим решение
Произведение у(х2+1)=0 при у = 0; так как при этом значении у дифференциальное уравнение не теряет числового смысла, то у = 0 — решение уравнения. Но оно входит в решение Подставив в общее решение значения у=3 и х =2Ö2, получим 3=С•3, откуда С=1. Частное решение уравнения, удовлетворяющее данному условию, имеет вид Пример 3. Решить уравнение 2х sin ydx +(х2+3) cos ydy=0. Найти частное решение, удовлетворяющее условию у =p/2 при х=1. Решение. Разделим каждый член уравнения на произведение (х2 • +3)sin y:
Интегрируя, находим
После потенцирования получим
Произведение (х2 + 3) sin у = 0 при sin у = 0, так как при этом значении дифференциальное уравнение не теряет числового смысла, то sin у=0 – решение уравнения. Но оно входит в интеграл Подставив в общий интеграл значения у=p/2 и х=1, получим 1=С/(1+3), откуда С = 4. Частный интеграл уравнения, удовлетворяющий данному условию, имеет вид sin у = 4/(х2 + 3). Пример 4. Решить уравнение еу (1 + х2) dy - 2x(1+еу) dx =0. Найти частное решение, удовлетворяющее условию у=0 при х=0. Решение. Перенесем второй член уравнения в правую часть и разделим обе части на произведение (1+еу)(1+х2):
Интегрируя, находим
После потенцирования получим общий интеграл уравнения: 1 + еу = С (1 + х2). Подставив в общий интеграл значения у=0 и х=0, получим 1+1=С, откуда С=2. Частный интеграл уравнения, удовлетворяющий данному условию, имеет вид 1+еу=2(1+х2).
Вопросы для самопроверки
1. Какое уравнение называется дифференциальным? 2. Дайте определение дифференциального уравнения первого порядка. 3. Дайте определение общего решения и общего интеграла дифференциального уравнения первого порядка. 4. Дайте определение частного решения и частного интеграла дифференциального уравнения первого порядка. 5. Решите дифференциальные уравнения и найдите частные решения (частные интегралы), удовлетворяющие данным условиям: а) (ху2 + х) dx - (у – х2у) dy =0; у = 1 при х = 2. б) ех (1+еу) dx + еу(1 + ex) dy = 0; у=0 при х=0, 6. Найдите частные решения (частные интегралы) дифференциального уравнения, удовлетворяющие данным условиям: а) у' = у3/х3; у =Ö2 при х =Ö3; б) у' tg х = 1 +у, у = - 1/2 при х = p/6.
Ответы. 5. а) (1 + у2)(1 - х3) = С, (1 + у2)(1 - х3) = -6; (1 + еу)(1 - ех) = С, (1 + еу)(1 - ех) = 4. 6. а) у2=6 х2/(х2 +6); б) у=sin х –1.
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 283; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.117.1 (0.006 с.) |


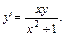 Найти частное решение, удовлетворяющее условию у = 3 при х = 2Ö2.
Найти частное решение, удовлетворяющее условию у = 3 при х = 2Ö2. то
то 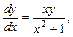 откуда (х2+1)dy=хуdх. Разделим обе части уравнения на произведение у(х2 - 1):
откуда (х2+1)dy=хуdх. Разделим обе части уравнения на произведение у(х2 - 1):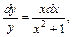
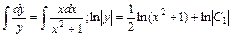
 откуда
откуда 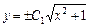 , или
, или 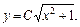 где С= + С1.
где С= + С1.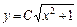 .
.
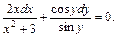
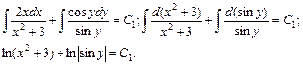
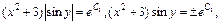 или
или 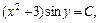 где
где 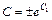 . Отсюда
. Отсюда 
 при С=0. Значит, общий интеграл уравнения имеет вид
при С=0. Значит, общий интеграл уравнения имеет вид