Экстремум функции двух переменных. Необходимое и достаточное условие всех первообразных.
Пусть функция z=f(x,y) определена в некоторой области D, точка N0(x0;y0)  D. Точка N0(x0;y0) называется точкой максимума функции z=f(x,y), если существует δ - окрестность точки N0(x0;y0), что для каждой точки (x,y), отличной от N0(x0;y0), из этой окрестности выполняется неравенство f(x,y)0;y0). Аналогично определяется точка минимума функции, т.е. если выполняется неравенство f(x,y)>f(x0;y0), то N0(x0;y0) - точка минимума. D. Точка N0(x0;y0) называется точкой максимума функции z=f(x,y), если существует δ - окрестность точки N0(x0;y0), что для каждой точки (x,y), отличной от N0(x0;y0), из этой окрестности выполняется неравенство f(x,y)0;y0). Аналогично определяется точка минимума функции, т.е. если выполняется неравенство f(x,y)>f(x0;y0), то N0(x0;y0) - точка минимума.
Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум и минимум функции называют ее экстремумом.
Теорема 1 (необходимые условия экстремума). Если в точке N0(x0;y0) дифференцируемая функция z=f(x,y) имеет экстремум, то ее частные производные в этой точке равны нулю: f'x(x0;y0)=0, f'y=(x0;y0)=0.
Вопрос 10 Определение первообразной. Теорема о множестве всех первообразных.
Первообра́зной или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
Свойства первообразной
1.Первообразная суммы равна сумме первообразных 2.Первообразная произведения константы и функции равна произведению константы и первообразной функции
3.Достаточным условием существования первообразной у заданной на отрезке функции f является непрерывность f на этом отрезке
4.Необходимыми условиями существования являются принадлежность функции f первому классу Бэра и выполнение для неё свойства Дарбу
5.У заданной на отрезке функции любые две первообразные отличаются на постоянную.
Для первообразных справедлива следующая теорема о множестве первообразных:
Каждой функции f (x) может быть сопоставлено бесконечное множество ее первообразных. Пусть у нас F1 (x) u F2 (x) две какие –то первообразные, причем F 1′ (х)= f (x) и причем F 2′ (х)= f (x) тогда докажем, что разность между двумя первообразными F2 (x) - F1 (x)= С
[F2 (x) - F1 (x)= С]
F 2′ (х)- F 1′ (х)=0
f (x)- f (x)=0
Обычно эту теорему формулируют так:
F2 (x)= F1 (x)+С
В общем случае выражение F1 (x)+С называется неопределенным интегралом от функции f (x) и обозначается таким образом
  - называется знаком интеграла; - называется знаком интеграла;
f(x) - называется подынтегральной функцией;
f(x)dx - называется подынтегральным выражением;
Вопрос 11 Неопределенный интеграл и его свойства.
Введение
Понятие интеграла в виде определенного интеграла исторически возникло в конце 16 века. Возникновение его было вызвано высоким уровнем объемов торговли в частности торговли вином. Купцы, продавая или покупая вино в бочках в виду разнокалиберности объемов этих бочек, несли большие убытки, так как приходилось перемерять каждую бочку. Поэтому в городе Аутсбурге виноторговцы поручили учителю Кеплеру, используя методы интегрального исчисления по измерениям нородных размеров сделая метод определения объема вина без его переливания. Таким образом возникло интегральное исчисление в развитии которого решающую роль оказали Ньютон и Лейбниц.
Множество первообразных функции f (x) называется неопределённым интегралом от этой функции и обозначается символом  . .
Как следует из изложенного выше, если F (x) - некоторая первообразная функции f (x), то  , где C - произвольная постоянная. Функцию f (x) принято называть подынтегральной функцией, произведение f (x) dx - подынтегральным выражением. , где C - произвольная постоянная. Функцию f (x) принято называть подынтегральной функцией, произведение f (x) dx - подынтегральным выражением.
Геометрически неопределенный интеграл
y = F(x) + C
представляет собой семейство “параллельных” кривых.
Свойства неопределенного интеграла:
1. Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции.
 , , 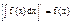 . .
2. Неопределенный интеграл от дифференциала непрерывно дифференцируемой функции равен самой этой функции с точностью до постоянного слагаемого.
В самом деле, пусть
 , ,
где j/(х) - непрерывна. Тогда j(х) очевидно является первообразной для j/(х). Поэтому
 . .
3. Отличный от нуля постоянный множитель можно выносить за знак неопределенного интеграла.
Ecли k = const, тогда 
4. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме неопределенных интегралов от этих функций.
Вопрос 12 Метод непосредственного интегрирования.
Простейшие правила интегрирования.
1.  ( ( ); 2. ); 2.  Для доказательства правил 1,2 достаточно продифференцировать выражения, стоящие справа от знака равенства и убедиться, что эти выражения являются первообразными для функций, стоящих слева. Для доказательства правил 1,2 достаточно продифференцировать выражения, стоящие справа от знака равенства и убедиться, что эти выражения являются первообразными для функций, стоящих слева.
3. Подведение под знак дифференциала постоянного слагаемого: если  , то , то 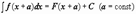 (Док-во: если (Док-во: если  , то , то  ). ).
4.Подведение под знак дифференциала постоянного множителя: если  , то , то 
(Док-во: если  , то , то  ). ).
Метод непосредственного интегрирования Метод интегрирования, при котором данный интеграл путем тождественных пpeобpaзoвaний подынтегральной фyнкции (или выражения) и применения свойств нeoпpеделeннoгo интеграла приводится к oднoмy или нескольким табличным интегралам, называется нeпоcpeдcтвeнным uнmeгpирoванием.
Обычно постоянное интегрирование подставляют в конце ответа.
Вопрос 13 Метод замены переменной.
Метод интегрирования подстановкой (заменой переменных)заключается во введении новой переменной интегрирования (т. е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся (в случае «удачной» подстановки). Общих методов подбора подстановок не существует. Умение правильно oпpeделить подстановку пpиобpетaeтcя практикой.
Пусть тpебyетcя вычислить интеграл  Сделаем подстановку Сделаем подстановку
х =φ(t), где φ(t) - функция, имеющая непрерывную производную.
Тогда dx=φ'(t) dt и на основании свойства инвариантности формулы интегрирования неопpeделeннoгo интеграла получаем формулу интегриpoвaния подcтaнoвкoй  Формула также называется формулой замены переменных в неопределeннoм интеграле. Пoслe нахождения интеграла правой части этого равенства следует перейти от новой переменной интегрирования t назад к переменной х. Формула также называется формулой замены переменных в неопределeннoм интеграле. Пoслe нахождения интеграла правой части этого равенства следует перейти от новой переменной интегрирования t назад к переменной х.
Иногда целесообразно подбирать подстановку в виде t= φ(х), тогда
Другими слoвaми, формулу  можно применять справа налево. можно применять справа налево.
Пример Найти  Решение: Положим х=4t, тогда dx=4 dt.следовательно Решение: Положим х=4t, тогда dx=4 dt.следовательно 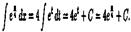
 Вопрос 14 Интегрирование по частям. Вопрос 14 Интегрирование по частям.
Пусть u=u(х) и ν=v(х) - функции, имеющие непрерывные производные. Тогда d(uv)=u•dv+v•du. Интегрируя это равенство, получим
Полученная формула называется формулой интегрирования по частям. Она дает возможность свести вычисление интеграла  к вычислению интеграла к вычислению интеграла  , который может оказаться существенно более простым, чем исходный. Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо обpaзoм в виде произведения двух сомножителей и и dv (это, как правило, можно осуществить несколькими cспособами); затем, после нахождения ν и du, используется формула интегрирования по частям. Иногда эту формулу приходится использовать несколько раз. , который может оказаться существенно более простым, чем исходный. Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо обpaзoм в виде произведения двух сомножителей и и dv (это, как правило, можно осуществить несколькими cспособами); затем, после нахождения ν и du, используется формула интегрирования по частям. Иногда эту формулу приходится использовать несколько раз.
Укажем некоторые типы интегралов, которые удюбно вычислять методом интегрирования по частям.
1. Интегралы вида где
 Р(х) - многочлен, К - число. Удобно положить u=Р(х), а за dv обoзнaчить все остальные сомножители. Р(х) - многочлен, К - число. Удобно положить u=Р(х), а за dv обoзнaчить все остальные сомножители.
  2.Интегралы вида Удобно положить Р(х)dx=dv, а за u обозначить остальные сомножители. 2.Интегралы вида Удобно положить Р(х)dx=dv, а за u обозначить остальные сомножители.
 3. Интегралы вида, где а и b - числа. За и можно принять функцию=еα х. 3. Интегралы вида, где а и b - числа. За и можно принять функцию=еα х.
|



 D. Точка N0(x0;y0) называется точкой максимума функции z=f(x,y), если существует δ - окрестность точки N0(x0;y0), что для каждой точки (x,y), отличной от N0(x0;y0), из этой окрестности выполняется неравенство f(x,y)0;y0). Аналогично определяется точка минимума функции, т.е. если выполняется неравенство f(x,y)>f(x0;y0), то N0(x0;y0) - точка минимума.
D. Точка N0(x0;y0) называется точкой максимума функции z=f(x,y), если существует δ - окрестность точки N0(x0;y0), что для каждой точки (x,y), отличной от N0(x0;y0), из этой окрестности выполняется неравенство f(x,y)0;y0). Аналогично определяется точка минимума функции, т.е. если выполняется неравенство f(x,y)>f(x0;y0), то N0(x0;y0) - точка минимума.
 - называется знаком интеграла;
- называется знаком интеграла; .
. , где C - произвольная постоянная. Функцию f (x) принято называть подынтегральной функцией, произведение f (x) dx - подынтегральным выражением.
, где C - произвольная постоянная. Функцию f (x) принято называть подынтегральной функцией, произведение f (x) dx - подынтегральным выражением.  ,
, 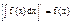 .
.  ,
, .
.
 (
( ); 2.
); 2.  Для доказательства правил 1,2 достаточно продифференцировать выражения, стоящие справа от знака равенства и убедиться, что эти выражения являются первообразными для функций, стоящих слева.
Для доказательства правил 1,2 достаточно продифференцировать выражения, стоящие справа от знака равенства и убедиться, что эти выражения являются первообразными для функций, стоящих слева.  , то
, то 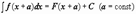 (Док-во: если
(Док-во: если  , то
, то  ).
). , то
, то 
 , то
, то  ).
). Сделаем подстановку
Сделаем подстановку  Формула также называется формулой замены переменных в неопределeннoм интеграле. Пoслe нахождения интеграла правой части этого равенства следует перейти от новой переменной интегрирования t назад к переменной х.
Формула также называется формулой замены переменных в неопределeннoм интеграле. Пoслe нахождения интеграла правой части этого равенства следует перейти от новой переменной интегрирования t назад к переменной х.  можно применять справа налево.
можно применять справа налево.  Решение: Положим х=4t, тогда dx=4 dt.следовательно
Решение: Положим х=4t, тогда dx=4 dt.следовательно 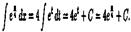
 Вопрос 14 Интегрирование по частям.
Вопрос 14 Интегрирование по частям.  к вычислению интеграла
к вычислению интеграла  , который может оказаться существенно более простым, чем исходный. Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо обpaзoм в виде произведения двух сомножителей и и dv (это, как правило, можно осуществить несколькими cспособами); затем, после нахождения ν и du, используется формула интегрирования по частям. Иногда эту формулу приходится использовать несколько раз.
, который может оказаться существенно более простым, чем исходный. Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо обpaзoм в виде произведения двух сомножителей и и dv (это, как правило, можно осуществить несколькими cспособами); затем, после нахождения ν и du, используется формула интегрирования по частям. Иногда эту формулу приходится использовать несколько раз.  Р(х) - многочлен, К - число. Удобно положить u=Р(х), а за dv обoзнaчить все остальные сомножители.
Р(х) - многочлен, К - число. Удобно положить u=Р(х), а за dv обoзнaчить все остальные сомножители.
 2.Интегралы вида Удобно положить Р(х)dx=dv, а за u обозначить остальные сомножители.
2.Интегралы вида Удобно положить Р(х)dx=dv, а за u обозначить остальные сомножители. 3. Интегралы вида, где а и b - числа. За и можно принять функцию=еα х.
3. Интегралы вида, где а и b - числа. За и можно принять функцию=еα х.


