
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Степенной ряд. Признаки сходимости. Область сходимости.Содержание книги
Поиск на нашем сайте
Степенной ряд с одной переменной — это формальное алгебраическое выражение вида:
в котором коэффициенты an берутся из некоторого кольца R. Для степенных рядов есть несколько теорем, описывающих условия и характер их сходимости. Первая теорема Абеля: Пусть ряд
Обращая эту теорему, получаем, что если степенной ряд расходится при x = x0, он расходится при всех x, таких что | x | > | x0 |. Из первой теоремы Абеля также следует, что существует такой радиус круга R (возможно, нулевой или бесконечный), что при | x | < R ряд сходится абсолютно (и равномерно по x на компактных подмножествах круга | x | < R), а при | x | > R — расходится. Это значение R называется радиусом сходимости ряда, а круг | x | < R — кругом сходимости. Формула Коши-Адамара: Значение радиуса сходимости степенного ряда может быть вычислено по формуле: (По поводу определения верхнего предела
Если у ряда G(x) свободный член нулевой, тогда
Вопрос о сходимости ряда в точках границы | x | = R круга сходимости достаточно сложен и общего ответа здесь нет. Вот некоторые из теорем о сходимости ряда в граничных точках круга сходимости: Признак Д’Аламбера: Если при n > N и α > 1 выполнено неравенство
тогда степенной ряд Признак Дирихле: Если все коэффициенты степенного ряда Вторая теорема Абеля: Пусть степенной ряд сходится в точке x = x0. Тогда он сходится равномерно по x на отрезке, соединяющем точки 0 и x0. Сумма степенного ряда как функция комплексного параметра x является предметом изучения теории аналитических функций. 51. ряд Маклорена … Ряды Маклорена некоторых функций Экспонента:
Натуральный логарифм: для всех Биномиальное разложение:
для всех
В частности: Квадратный корень:
для всех
для всех | x | < 1 Конечный геометрический ряд:
Тригонометрические функции:
для всех
Гиперболические функции:
для всех
для всех
для всех 52. Ряд Тейлора… Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций. Определение Пусть функция f(x) бесконечно дифференцируема в некоторой окрестности точки a. Формальный ряд называется рядом Тейлора функции f в точке a. Свойства Если f есть аналитическая функция, то её ряд Тейлора в любой точке a области определения f сходится к f в некоторой окрестности a. Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности a. Например, Коши предложил такой пример:
У этой функции все коэффициенты ряда Тейлора равны нулю. Формула Тейлора Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки. Теорема: Þ Пусть функция f(x) имеет n + 1 производную в некоторой окрестности точки a, U(a,ε) Þ Пусть Þ Пусть p — произвольное положительное число, тогда:
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша). Различные формы остаточного члена В форме Лагранжа:
В форме Коши:
Ослабим предположения: Пусть функция f(x) имеет n − 1 производную в некоторой окрестности точки a И n производную в самой точке a, тогда:
Применение рядов для приближенного вычисления определенных интегралов
Вычислить определённый интеграл
Так как
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.7.53 (0.01 с.) |


 сходится в точке x0. Тогда этот ряд сходится абсолютно в круге | x | < | x0 | и равномерно по x на любом компактном подмножестве этого круга.
сходится в точке x0. Тогда этот ряд сходится абсолютно в круге | x | < | x0 | и равномерно по x на любом компактном подмножестве этого круга.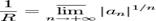
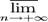 Пусть F(x) и G(x) — два степенных ряда с радиусами сходимости RF и RG. Тогда
Пусть F(x) и G(x) — два степенных ряда с радиусами сходимости RF и RG. Тогда

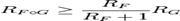
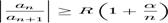
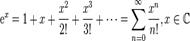
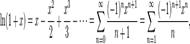
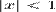
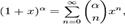
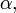 где
где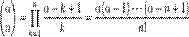
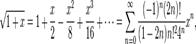
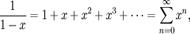
 для всех
для всех 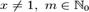

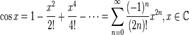
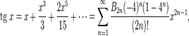
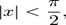 где B2n — Числа Бернулли
где B2n — Числа Бернулли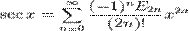
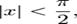 для всех
для всех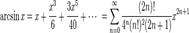
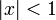 для всех
для всех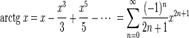

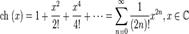
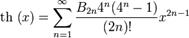


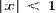
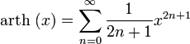


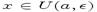
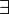 точка
точка 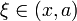 при x < a или
при x < a или  при x > a:
при x > a:
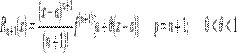
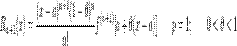
 — остаточный член в асимптотической форме (в форме Пеано, в локальной форме)
— остаточный член в асимптотической форме (в форме Пеано, в локальной форме)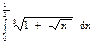 с точностью до 0,001, разложив подынтегральную функцию в степенной ряд, и затем проинтегрировать его почленно.
с точностью до 0,001, разложив подынтегральную функцию в степенной ряд, и затем проинтегрировать его почленно.
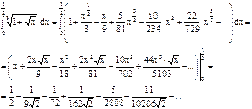
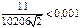 , то для требуемой точности достаточно первых пяти членов полученного ряда:
, то для требуемой точности достаточно первых пяти членов полученного ряда:



