
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
З а м е ч а н и Е. Нет общего метода интегрирования уравнения первого порядка. Обычно рассматривают некоторые отдельные типы таких уравнений, для каждого из которых дается свой способ.Содержание книги
Поиск на нашем сайте
Однородные дифференциальные уравнения второго порядка Уравнение второго порядка Однородное уравнение второго порядка: a2y'' + a1y' + a0y = 0 интегрируется следующим образом: Пусть λ1,λ2 — корни характеристического уравнения. a2λ2 + a1λ + a0 = 0, Являющегося квадратным уравнением. Вид общего решения однородного уравнения зависит от значения дискриминанта: при Δ > 0 уравнение имеет два различных вещественных корня
Общее решение имеет вид: при Δ = 0 — два совпадающих вещественных корня
Общее решение имеет вид: y(t) = c1e^αt + c2te^αt при Δ < 0 существуют два комплексно сопряженных корня
Общее решение имеет вид: y(t) = c1e^αt cos(βt) + c2e^αt sin(βt) Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами Дифференциальное уравнение где коэффициенты Если Если I. Рассмотрим однородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами:
Общим решением уравнения (17) является функция
(18) где Фундаментальной системой решений называется всякая система линейно независимых решений, содержащая столько функций, каков порядок дифференциального уравнения. Функции Кратко критерий линейной независимости может быть сформулирован следующим образом: функции
отличен от нуля. В противном случае функции линейно зависимы.
Числовые ряды. Определение ряда и его сходимостьВ настоящей главе обобщим понятие суммы на некоторые случаи бесконечного числа слагаемых и изучим свойства таких сумм. Определение 1. Пусть задана последовательность чисел. а1, а2, а3,..., аn,... (1.1) Выражение вида
называется рядом, а число аn - его n-ным членом, n = 1,2,....
Сразу же заметим, что в нашем случае (1.2) - числовой ряд. Если же последовательность есть последовательность функций, то ряд называется функциональным (аn = fn(x), n = 1,2,...). Примеры. аn = а×qn-1,. Понятно, что изучение функциональных рядов всегда можно свести к изучению числовых рядов, зафиксировав х = х0. Ряд (1.2) считается заданным, если мы знаем его общий член аn (то есть член, стоящий на n-ном месте). Из теории последовательностей мы знаем, что аn выражается как функция номера n. Определение 2. Конечная сумма первых n членов ряда называется n-й частичной суммой, а оставшиеся члены, начиная с n + 1, написанные в том же порядке, что и в данном ряду, называется n-ным остатком ряда.
(1.3) Sn - n-ная частичная сумма (n = 1,2,...,k) Rn = an+1 + an+2 +... + an+i +..., (1.4) Rn - остаток ряда. Определение 3. Ряд Если ряд сходится, то
Если Необходимый признак сходимости ряда. Числовые ряды - выражение типа
(1)
Ряд считается заданным, если задан общий член. Сумма первых n членов ряда называется n-ной суммой членов ряда.
- называют суммой ряда (1) и говорят, что ряд сходится.
Если предел не существует, то ряд (1) считается расходящимся. Свойства рядов: 1) Если ряд (1) сходится, то сходится и ряд. 2) Если ряд (1) сходится и ряд 3) Если к ряду (1) прибавить (или отбросить) конечное число членов, то полученный ряд и ряд (1) сходящиеся и расходящиеся одновременно. Теорема (необходимый признак сходимости числового ряда). Если ряд (1) сходится, то его общий член стремится к нулю, то есть Если не выполняется, то расходится. Достаточное условие расходимости ряда: если предел Необходимый признак сходимости ряда недостаточен для сходимости, поскольку существуют ряды, которые расходятся, но необходимый признак сходимости для них выполняется.
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 253; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.95.129 (0.007 с.) |

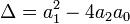
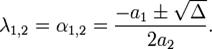
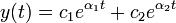
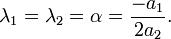
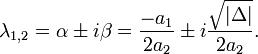
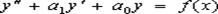 (16)
(16)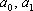 – постоянные, называется линейным дифференциальным уравнением второго порядка с постоянными коэффициентами.
– постоянные, называется линейным дифференциальным уравнением второго порядка с постоянными коэффициентами.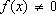 , то уравнение (16) называется неоднородным.
, то уравнение (16) называется неоднородным.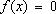 , то уравнение (16) называется однородным.
, то уравнение (16) называется однородным.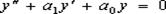 (17)
(17)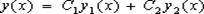
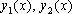 – фундаментальная система решений уравнения (17).
– фундаментальная система решений уравнения (17).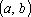 , если существуют постоянные числа
, если существуют постоянные числа 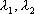 , не все равные нулю, такие что
, не все равные нулю, такие что 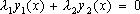 для любых
для любых 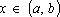 . Если же указанное тождество выполняется только в случае, когда
. Если же указанное тождество выполняется только в случае, когда 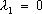 и
и 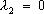 , то функции
, то функции 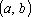 .
.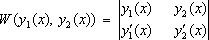
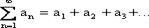 (1.2)
(1.2)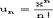
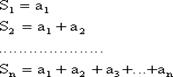
 называется сходящимся, если последовательность его частичных сумм сходится. Если ряд не сходится, то говорят, что он расходится.
называется сходящимся, если последовательность его частичных сумм сходится. Если ряд не сходится, то говорят, что он расходится.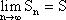 называется его суммой.
называется его суммой. . (1.5)
. (1.5)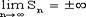 , то
, то 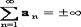 .
.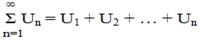
 - члены ряда,
- члены ряда,  - общий член ряда.
- общий член ряда.

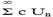 (с - const)
(с - const)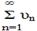 сходится, то
сходится, то  сходится.
сходится.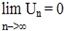 .
. или этот предел не существует, то ряд расходится.
или этот предел не существует, то ряд расходится.


