
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановокСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотри интегралы, содержащие квадратный трехчлен:
Выделив полный квадрат под корнем, получим один из трех интегралов:
1.
2.
3.
Интегрирование простейших иррациональных выражений .Класс иррациональных функций очень широк, поэтому универсального способа их интегрирования просто быть не может. В этой статье попытаемся выделить наиболее характерные виды иррациональных подынтегральных функций и поставить им в соответствие метод интегрирования. 1.Используя метод непосредственного интегрирования, достаточно просто находятся неопределенные интегралы вида, где p – рациональная дробь, k и b – действительные коэффициенты. 2.Бывают случаи, когда уместно использование метода подведения под знак дифференциала. Например, при нахождении неопределенных интегралов вида
3.Достаточно часто приходится иметь дело с неопределенными интегралами вида В этом случае выделяем полный квадрат под знаком корня:
Понятие интегральной суммы Понятие интегральной суммы естественно обобщается на случай знакопеременной функции.
25 Свойства определенного интеграла
1) Если f (x) = c = const, то 3) Если f1 (x) и f2 (x) интегрируемые на [a; b], то: 4) Если в определенном интеграле поменять местами пределы интегрирования, то интеграл только изменит свой знак на противоположный. 5) Определенный интеграл с одинаковыми пределами интегрирования равен нулю. 6) Если f (x) - интегрируема в любом из промежутков [a; b], [a; c], [c; b], то: 8) Если f (x), g (x) - интегрируемые и f (x) ³ g (x) для x Î [a; b], b> a, то: 9) Если f (x) - интегрируема и m £ f (x) £ M, для x Î [a; b], b> a, то 10) (Теорема о среднем): Если ф-ия f (x) - непрерывная для x Î [a; b], b> a, то найдется такая точка x = c Î [a; b], что:
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 708; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.249.188 (0.007 с.) |


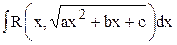 .
. ,
,  ,
,  . Все они вычисляются с помощью тригонометрических подстановок.
. Все они вычисляются с помощью тригонометрических подстановок.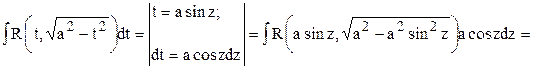
 .
.
 .
.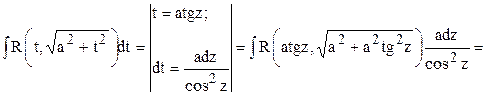
 .
.
 , где p – рациональная дробь.
, где p – рациональная дробь. , где p и q – действительные коэффициенты.
, где p и q – действительные коэффициенты. и используем формулу из таблицы неопределенных интегралов
и используем формулу из таблицы неопределенных интегралов  .
. , где M, N, p и q – действительные коэффициенты, очень схоже с интегрированием простейших дробей третьего типа: выполняется подведение под знак дифференциала, затем выделяется полный квадрат подкоренного выражения и применяются формулы из таблицы первообразных
, где M, N, p и q – действительные коэффициенты, очень схоже с интегрированием простейших дробей третьего типа: выполняется подведение под знак дифференциала, затем выделяется полный квадрат подкоренного выражения и применяются формулы из таблицы первообразных


