
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Темы «Интегральное исчисление функции одной переменной. Ряды»
1. Первообразная функция, определение и теоремы. 2. Неопределенный интеграл и его свойства. Таблица основных интегралов. 3. Метод непосредственного интегрирования в неопределенном интеграле. 4. Метод замены переменной в неопределенном интеграле. 5. Метод интегрирование по частям для неопределенного интеграла. Классы интегралов, берущихся по частям. 6. Интегрирование рациональных выражений, содержащих квадратный трехчлен. 7. Интегрирование иррациональных выражений, содержащих квадратный трехчлен. 8. Интегрирование рациональных функций: сведение неправильных рациональных дробей к правильным, разложение дробно-рациональных выражений на простейшие дроби. 9. Интегрирование простейших рациональных дробей. 10. Интегрирование иррациональных функций: случаи сведения к интегрированию рациональных функций. 11. Применение подстановок Эйлера к интегрированию иррациональных выражений. 12. Интегрирование тригонометрических и других трансцендентных функций. 13. Интегралы, не выражающиеся в элементарных функциях. 14. Понятие об уравнении поверхности. Плоскость в пространстве. Различные уравнения плоскости: общее, в отрезках, нормальное. Уравнение плоскости, проходящей через три данных точки. 15. Прямая в пространстве. Прямая как линия пересечения двух плоскостей. Канонические уравнения плоскости. Параметрические уравнения плоскости. Приведение уравнений прямой к каноническим. 16. Угол между двумя плоскостями, между двумя прямыми, между прямой и плоскостью и их нахождение. Условия параллельности двух прямых, двух плоскостей, прямой и плоскости. Условия перпендикулярности двух прямых, двух плоскостей, прямой и плоскости. 17. Поверхности второго порядка: сфера, эллипсоид. Исследование их формы и построение. 18. Однополостный и двуполостный гиперболоиды. Исследование их формы и построение. 19. Эллиптический и гиперболический параболоиды. Исследование их формы и построение. 20. Цилиндрические и конические поверхности. Исследование их формы и построение. 21. Задачи, приводящие к понятию определенного интеграла. Определенный интеграл как предел интегральных сумм. 22. Основные свойства определенного интеграла. Формула Ньютона-Лейбница. 23. Замена переменной и интегрирование по частям в определенном интеграле. 24. Приложения определенного интеграла для вычисления площади, длины дуги, площади поверхности вращения, объема. 25. Несобственные интегралы с бесконечными пределами интегрирования, интегралы от неограниченных функций. 26. Числовые ряды: основные понятия, необходимые условия сходимости ряда. Остаток ряда. 27. Ряды с положительными членами и признаки их сходимости: признаки сравнения, Даламбера, Коши (радикальный и интегральный). 28. Знакочередующиеся ряды, признак Лейбница. 29. Степенные ряды и область их сходимости. 30. Разложение функций в степенной ряд. Разложение некоторых элементарных функций ( 31. Применение степенных рядов к приближенным вычислениям значений функций, интегралов, пределов. 32. Системы ортогональных функций. Примеры. 33. Тригонометрические ряды и их сходимость. Ряды Фурье. Формулы для вычисления коэффициентов ряда Фурье. 34. Ряды Фурье для четных и нечетных периодических функций. Практическое занятие № 44 Тема занятия « Функции нескольких переменных. Частные производные функции нескольких переменных » Цель занятия: изучить определения частных производных и правила их нахождения. Организационная форма занятия: практикум. Компетенции, формируемые на занятии: - способность и готовность анализировать социально-значимые проблемы и процессы, использовать на практике методы гуманитарных, естественнонаучных, медико-биологических, и клинических наук в различных видах профессиональной и социальной деятельности (ОК-1). Формирование у будущих специалистов этой компетенции на занятии предполагает обучение студентов - сформулировать гипотезу и проверить ее в дальнейшем; - анализировать ситуации и делать выводы; - ставить новые вопросы и видеть проблемы в традиционных ситуациях; - абстрагировать содержание и выделять существенное. Вопросы, выносимые на обсуждение 1. Функции нескольких переменных, основные определения. 2. Частные производные первого порядка. 3. Частные производные второго и более высоких порядков. 4. Теорема о независимости смешанных производных от порядка дифференцирования. 5. Производная сложной функции. Полная производная. Методические рекомендации Для подготовки к занятию дома 1. Прочитайте конспект лекции, соответствующий теме занятия. Запомните основные определения. 2. Изучите рекомендуемую литературу по вопросам, выносимым на обсуждение. 3. Найдите ответы на теоретические задания для развития и контроля владения компетенциями. Подготовьтесь к ответам на эти вопросы на занятии. 4. Законспектируйте ответы на теоретические задания, которые не содержатся в Вашем конспекте лекции по указанной теме. 5. Изучите разобранные примеры решения типовых задач и законспектируйте их решение в рабочую тетрадь. На занятии по указанию преподавателя 1. Дайте ответы на вопросы из теоретических заданий для развития и контроля владения компетенциями. 2. В рабочей тетради и на доске решите практические задания для развития и контроля владения компетенциями из заданий, решаемых в аудитории. 3. Разберите с преподавателем вопросы, которые остались Вами не понятыми по теме этого занятия. 4. Сдайте выполненное ИДЗ №9 на проверку преподавателю. Дома 1. Закрепите полученные практические умения и навыки, решая практические задания для развития и контроля владения компетенциями из заданий для самостоятельной работы дома. 2. Пройдите репетиционное тестирование по пройденной теме. Рекомендуемая литература [1] глава 11 пп 11.1 - 11.3. [2] часть 1, глава VIII §§ 1 – 2. [3] глава 6 §§ 27, 30. [4] часть II занятия 37 – 39. [6] глава 12 § 1; § 6. [7] глава VIII §§1; 2; 6.
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ 1. Укажите область определения функции Решение. Аналитическое выражение 2. Найдите область определения функции Решение. Для того чтобы Все точки 3. Найдите частные производные первого порядка для функции Решение. Вычисляем частную производную функции по переменной
Аналогично, считая, что
4. Вычислите частные производные второго порядка для функции Решение. Воспользуемся найденными частными производными первого порядка
Заметим, что смешанные частные производные равны, т.е. 5. Для сложной функции Решение. Для нахождения частных производных для сложной формулы воспользуемся формулами Тогда получаем
В последние выражения вместо Замечание. Для случая большего числа переменных формулы нахождения частных производных обобщаются. Например, если
Если задана функция 6. Вычислите полную производную функции Решение. Воспользуемся формулой вычисления полной производной
Теоретические задания
|
||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 330; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.107.223 (0.007 с.) |
 ,
,  ,
,  ,
, 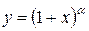 ,
,  ,
,  ,
,  ) в ряд Тейлора (Маклорена).
) в ряд Тейлора (Маклорена). .
.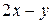 имеет смысл при любых значениях
имеет смысл при любых значениях  и
и  . Следовательно, областью определения функций является вся плоскость
. Следовательно, областью определения функций является вся плоскость 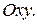

 имело действительное значение, нужно, чтобы под корнем стояло неотрицательное число, т.е.
имело действительное значение, нужно, чтобы под корнем стояло неотрицательное число, т.е. 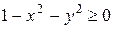 , или
, или  .
. ,координаты которых удовлетворяют указанному неравенству, лежат в круге радиуса
,координаты которых удовлетворяют указанному неравенству, лежат в круге радиуса  с центром в начале координат и на границе этого круга.
с центром в начале координат и на границе этого круга. .
.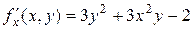 .
. .
. и
и  , которые сами являются функциями двух переменных
, которые сами являются функциями двух переменных  ;
; ;
; ;
; .
. .
. вычислите частные производные первого порядка.
вычислите частные производные первого порядка. и
и  . Вычисляем частные производные входящие
. Вычисляем частные производные входящие  ,
,  ,
,  ,
,  ,
, 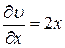 ,
,  .
.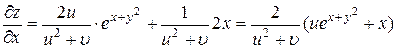 ,
, .
.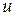 и
и  необходимо поставить
необходимо поставить  и
и  соответственно.
соответственно. - функция четырех аргументов
- функция четырех аргументов  а каждый из них зависит от
а каждый из них зависит от  ,
,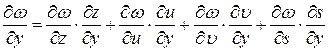 .
. , где
, где  в свою очередь зависят от одного аргумента
в свою очередь зависят от одного аргумента  то,
то, 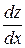 . Эта производная вычисляется по первой из приведенных формул:
. Эта производная вычисляется по первой из приведенных формул:  . Но так как
. Но так как  ; поэтому
; поэтому  . Эта формула носит название формулы для вычисления полной производной
. Эта формула носит название формулы для вычисления полной производной 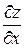 ).
). , если
, если  . Вычисляем
. Вычисляем  ,
,  ,
,  . Тогда подставляя в формулу, получаем следующий результат:
. Тогда подставляя в формулу, получаем следующий результат: .
.


