
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная и дифференциал функцииСодержание книги
Поиск на нашем сайте
Т.Н. Ерохина
СБОРНИК ЗАДАЧ И УПРАЖНЕНИЙ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
Учебное пособие Барнаул 2005 Т.Н. Ерохина
СБОРНИК ЗАДАЧ И УПРАЖНЕНИЙ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
Учебное пособие Барнаул 2005
Ерохина Т.Н. Сборник задач и упражнений по математике: учебное пособие.-Барнаул,2005,-46 С.
Учебное пособие составлено с учетом Государственного стандарта среднего профессионального образования. В пособии подобран теоретический и практический материал для освоения программы дисциплины «Математика». Материал изложен в доступной форме, с соблюдением должной математической строгости. Приводятся решения типовых примеров и задач, что способствует лучшему пониманию учебного материала. В конце каждой темы имеются упражнения для самостоятельной решения. Данный материал предназначен в первую очередь для студентов торгово-экономического колледжа дневной, заочной и дистанционной форм обучения. Может быть использован преподавателями и студентами других учебных заведений, а также для самостоятельного обучения. Рецензент: Л.В. Болгерт преподаватель информатики БТЭК © Издательство 2005 Содержание
Предисловие.................................................................................... 4 1 Предел функции.......................................................................... 5 Упражнения................................................................................ 10 2 Производная и дифференциал функции.............................. 11 Упражнения................................................................................ 26 3 Неопределенный интеграл...................................................... 30 Упражнения................................................................................ 36 4 Определенный интеграл.......................................................... 38 Упражнения................................................................................ 44 Список использованных источников....................................... 46
Предисловие
В учебном пособии раскрывается содержание основных понятий и теорем курса математического анализа на специально подобранных упражнениях и задачах. В каждом разделе приводятся краткие теоретические сведения, состоящие из определений и основных математических понятий. Первый раздел посвящен пределу функции, второй – производной функции, третий и четвертый – интегральному исчислению.
В пособии подобраны типовые задачи и приводятся их решения. В каждом разделе содержаться упражнения для самостоятельной работы. Пособие рекомендуется для практических занятий всех форм обучения БТЭК. Автор считает своим долгом выразить искреннюю признательность студентам и преподавателям, высказывающим критические замечания и предложения, способствующие улучшению данного пособия в будущем. Предел функции
Число а называется пределом числовой последовательности х1, х2, х3… хn, если для всякого сколь угодно малого положительного числа Е найдется такое положительное число N, что çхn – aç< Е при n>N. В этом случае пишут Число А называется пределом функции f (x) при х → а, если для любого сколь угодно малого Е > 0 найдется такое δ > 0, что çf(x) – Aç < Е при 0<çх – аç < δ.
Аналогично Условно записывают М – производное положительное число. В этом случае функция f(x) называется бесконечно большой при х→а. Если при х→а. Вычисление приделов основывается на следующих теоремах и их следствиях. Если существуют
Пример 1 Вычислить Воспользуемся теоремой о пределе разности и суммы, получим
Таким образом, для вычисления предела многочлена f (x) при х → х0 достаточно вместо переменной х поставить значение х0, к которому она стремится, и выполнить соответствующие действия, т.е.
Пример 2 Вычислить Предел отношения двух многочленов, Если q(х0) ≠ 0, то можно применить теорему о пределе частного. Здесь
Пример 3 Вычислить Если
Если же Разложим на множители числитель и знаменатель.
Пример 4 Вычислить Здесь I Способ решения: Для раскрытия неопределенности разложим числитель и знаменатель на множители, используя формулу:
D = b2 – 4ac дискриминант. Решим уравнение
Его корни
II Способ решения: Введем замену:
Пример 5 Вычислить
Имеет место неопределенность вида
Пример 6 Вычислить Данный предел представляет отношение многочленов По свойствам бесконечно больших функций
Пример 7 Вычислить В числителе
Пример 8 Вычислить Имеет место неопределенность вида
Упражнения Вычислить пределы (1.1-1.46): 1.1 1.4 1.7 1.10 1.13 1.16 1.19 1.22 1.25 1.28 1.31 1.34 1.38 1.41 1.44 Правила дифференцирования 1. 3.
Таблица производных
Пример 1 Найти производные функций: а) б) в) Решение: а) Применим правила дифференцирования.
Пример 2 Найти производные функций: а) б) Решение: Данные функции являются сложными степенными
б) Пример 3 Найти производные функции: а) б) в) Решение: а) Функция сложная
б) Функция сложная
в) Функция сложная
Упражнения Найти производные функции (2.1-2.43): 2.1 2.3 2.5 2.7 2.9 2.11 2.13 2.15 2.17 2.19 2.21 2.23 2.25 2.27 2.29 2.31 2.33 2.35. 2.37 2.39 2.41 2.43 Найти производные и дифференциалы функций (2.44-2.54): 2.44 2.46 2.48 2.50 2.52 2.54 Найти производные высших порядков (2.55-2.62) 2.55 2.56 2.57 2.58 2.59 2.60 2.61 2.62 Найти интервалы монотонности функций (2.63-2.70): 2.63 2.65 2.67 2.69 Исследовать с помощью первой производной функции на экстремум (2.71-2.78): 2.71 2.73 2.75 2.77 Исследовать с помощью второй производной функции на экстремум (2.79-2.85): 2.79 2.81 2.83 2.85 Найти точки перегиба и интервалы выпуклости и вогнутости следующих кривых (2.86-2.95): 2.86 2.88 2.90 2.92 2.94 Исследовать функции и построить их график (2.96-2.104): 2.96 2.99 2.102 Неопределенный интеграл
Функция F(х) называется первообразной для функции f (x), если Если функция f(х) имеет первообразную F(x), то она имеет бесконечное множество первообразных, причем все первообразные содержатся в выражении Неопределенным интегралом от функции f (x) называется совокупность всех ее первообразных.
Отыскание неопределенного интеграла называется интегрированием. Основные интегралы. 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) Методы интегрирования I. Непосредственное интегрирование: подынтегральное выражение путем преобразований и использования свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам. Пример 1 Вычислить Разделим числитель на знаменатель, получим
Пример 2 Найти Приведем подынтегральные выражения к степенным
Пример 3 Найти Раскроем скобки
Пример 4 Найти Преобразуем знаменатель
Проверим результат
Получили подынтегральную функцию, интеграл найден верно.
II. Замена переменной в неопределенном интеграле: замена переменной в неопределенном интеграле производится с помощью подстановок двух видов: 1)
2) Формула замены переменной при такой постановке:
Пример 5 Найти Приведем подынтегральное выражение к табличному с помощью замены
Пример 6 Найти Так как производная выражения
Пример 7 Найти Во многих случаях нет необходимости записывать, какое выражение мы принимаем за новую переменную.
III. Интегрирование по частям: интегрированием по частям называется нахождение интеграла по формуле
где При этом за U берется такая функция, которая при дифференцировании упрощается, а за Пример 8 Найти Положим
Пример 9 Найти Положим
Пример 10 Найти Положим
Вновь применим формулу интегрирования по частям. Положим Таким образом,
Так как в правой части стоит искомый интеграл, то перенесем его в левую часть получим
Упражнения Найти интегралы (3.1-3.61):
3.1 3.3 3.5 3.7 3.9 3.11 3.13 3.15 3.17 3.19 3.21 3.23 3.25 3.27 3.29 3.31 3.33 3.35 3.37 3.39 3.41 3.43 3.45 3.47 3.49 3.51 3.53 3.55 3.57 3.59 3.61
Определенный интеграл
Определенным интегралом от функции
Если функция Числа a и b называют нижним и верхним пределами интегрирования. Упражнения Вычислить интегралы (4.1-4.37): 4.1 4.4 4.7 4.10 4.13 4.16 4.19 4.22 4.25 4.28 4.31 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |


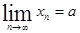 .
.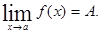
 , если çf(x)-Aç< Е при çхç>N.
, если çf(x)-Aç< Е при çхç>N.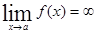 , если çf(x)ç>М при 0<çх-аç<δ, где
, если çf(x)ç>М при 0<çх-аç<δ, где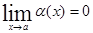 , то функция a(x) называется бесконечно малой
, то функция a(x) называется бесконечно малой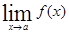 и
и 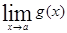 , то
, то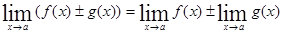 .
.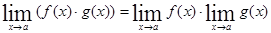 .
.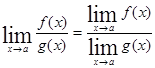 , если g(x)≠0.
, если g(x)≠0.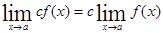 , где с=const.
, где с=const.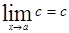 .
.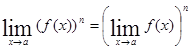 .
. .
.
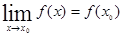
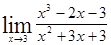 .
.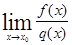 , где х0 – число.
, где х0 – число.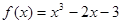 и
и 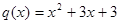 .Так как
.Так как  , то имеем:
, то имеем: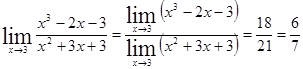 .
. .
.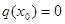 , то теорему о пределе частного применить нельзя. Тогда если
, то теорему о пределе частного применить нельзя. Тогда если 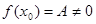 , то
, то .
. имеем неопределенность вида
имеем неопределенность вида 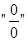 , в этом случае предел
, в этом случае предел 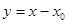 .
.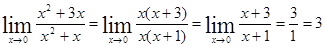 .
. .
.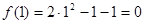 ,
, 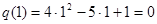 , имеет место неопределенность вида
, имеет место неопределенность вида 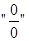 .
.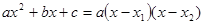 , где
, где 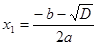 ;
;  корни квадратного уравнения.
корни квадратного уравнения.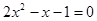 .
.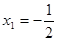 ;
; 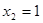 .
.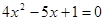 .
.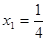 ;
;  .
. ,
, 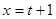 , так как
, так как 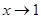 , то
, то 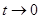 .
.
 .
. ,
, 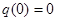 .
.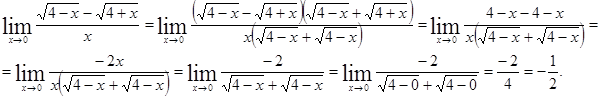
 .
. при
при 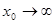 .
.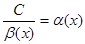 , где
, где  ,
,  - бесконечно большая функция,
- бесконечно большая функция,  - бесконечно малая функция.
- бесконечно малая функция. .
.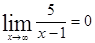 .
.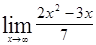 .
.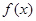 - бесконечно большая функция. По свойствам бесконечно больших функций
- бесконечно большая функция. По свойствам бесконечно больших функций 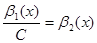 , где
, где  ,
, 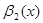 - бесконечно большие функции.
- бесконечно большие функции. .
.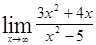 .
. . Вынесем в числителе и знаменателе аргумент со старшей степенью.
. Вынесем в числителе и знаменателе аргумент со старшей степенью.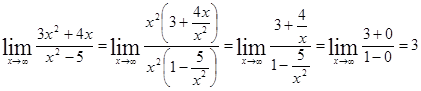 .
. ; 1.2
; 1.2 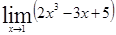 ; 1.3
; 1.3 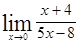 ;
;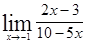 ; 1.5
; 1.5 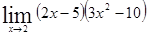 ; 1.6
; 1.6 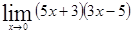 ;
;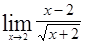 ; 1.8
; 1.8 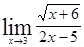 ; 1.9
; 1.9 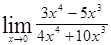 ;
;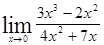 ; 1.11
; 1.11 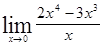 ; 1.12
; 1.12 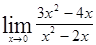 ;
;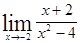 ; 1.14
; 1.14  ; 1.15
; 1.15 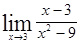 ;
; ; 1.17
; 1.17 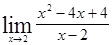 ; 1.18
; 1.18 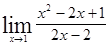 ;
;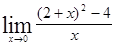 ; 1.20
; 1.20 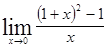 ; 1.21
; 1.21 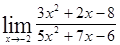 ;
; ; 1.23
; 1.23 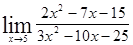 ; 1.24
; 1.24 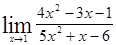 ;
; ; 1.26
; 1.26 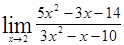 ; 1.27
; 1.27 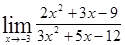 ;
;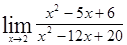 ; 1.29
; 1.29 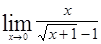 ; 1.30
; 1.30 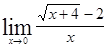 ;
;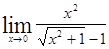 ; 1.32
; 1.32 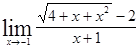 ;1.33
;1.33 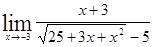 ;
;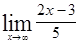 ; 1.35
; 1.35 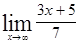 ; 1.36
; 1.36 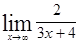 ; 1.37
; 1.37  ;
;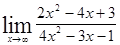 ; 1.39
; 1.39 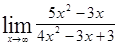 ; 1.40
; 1.40 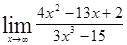 ;
;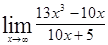 ; 1.42
; 1.42 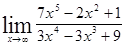 ; 1.43
; 1.43  ;
;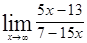 ; 1.45
; 1.45  ; 1.46
; 1.46 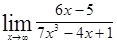 .
.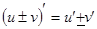 2.
2. 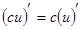 , где
, где 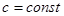
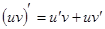 4.
4. 
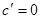 ,
, 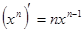
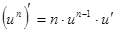
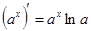
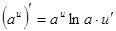
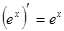
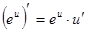
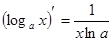

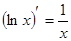
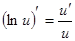
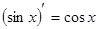

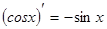
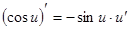
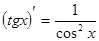

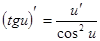
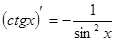
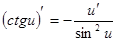
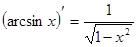
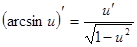
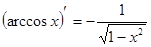
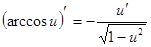
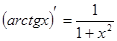
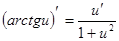
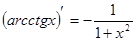

 - дифференциал функции
- дифференциал функции  , где
, где 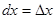 - дифференциал независимой переменной х.
- дифференциал независимой переменной х.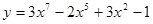 ;
;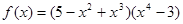 ;
;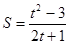 .
.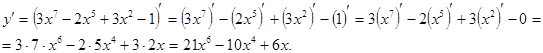
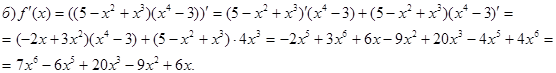

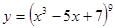 ;
;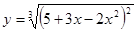 .
.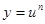 .
.
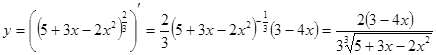 .
.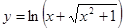 ;
;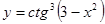 ;
; ;
;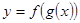 , где
, где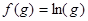 ,
,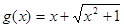 .
.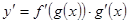
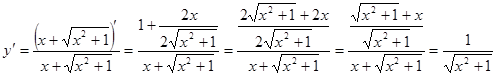 .
.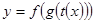 , где
, где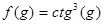 ,
,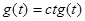 ,
,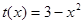 .
.
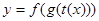 , где
, где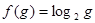 ,
,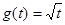 ,
, .
.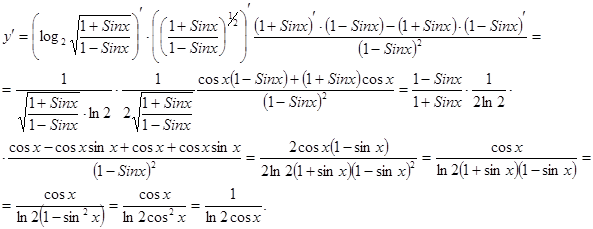
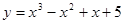 ; 2.2
; 2.2 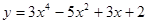 ;
;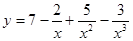 ; 2.4
; 2.4  ;
;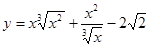 ; 2.6
; 2.6 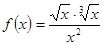 ;
;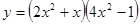 ; 2.8
; 2.8 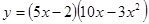 ;
;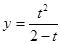 ; 2.10
; 2.10 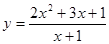 ;
; ; 2.12
; 2.12 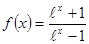 Найти
Найти  ;
;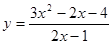 ; 2.14
; 2.14 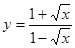 ;
;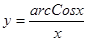 ; 2.16
; 2.16 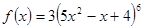 ;
;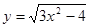 ; 2.18
; 2.18 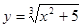 ;
;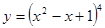 ; 2.20
; 2.20 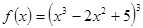 Найти
Найти 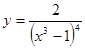 ; 2.22
; 2.22 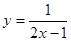 ;
;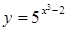 ; 2.24
; 2.24 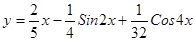 ;
;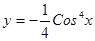 ; 2.26
; 2.26  ;
;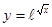 ; 2.28
; 2.28  ;
;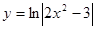 ; 2.30
; 2.30 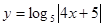 ;
;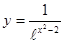 ; 2.32
; 2.32  Найти
Найти  ;
;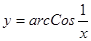 ; 2.34
; 2.34  Найти
Найти 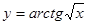 ; 2.36
; 2.36 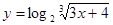 ;
;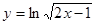 ; 2.38
; 2.38 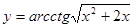 ;
;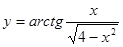 ; 2.40
; 2.40 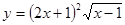 ;
; ; 2.42
; 2.42 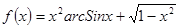 ;
; .
.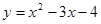 ; 2.45
; 2.45  ;
;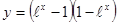 ; 2.47
; 2.47 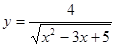 ;
; ; 2.49
; 2.49 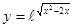 ;
;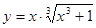 ; 2.51
; 2.51  ;
;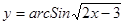 ; 2.53
; 2.53  ;
; .
.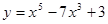 Найти
Найти 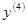 .
.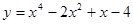 Найти
Найти 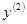 .
.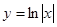 Найти
Найти 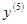 .
.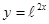 Найти
Найти 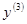 .
.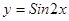 Найти
Найти 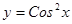 Найти
Найти 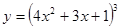 Найти.
Найти. 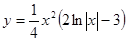 Найти.
Найти.  ; 2.64
; 2.64  ;
; ; 2.66
; 2.66 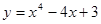 ;
; ; 2.68
; 2.68 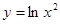 ;
;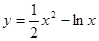 ; 2.70
; 2.70 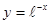 .
.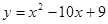 ; 2.72
; 2.72 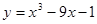 ;
; ; 2.74
; 2.74  ;
;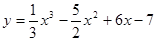 ; 2.76
; 2.76  ;
; ; 2.78
; 2.78  .
.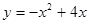 ; 2.80
; 2.80 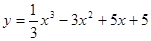 ;
;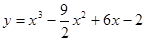 ; 2.82
; 2.82 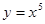 ;
;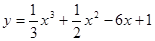 ; 2.84
; 2.84 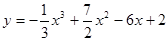 ;
; .
.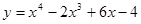 ;
;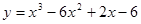 ; 2.89
; 2.89 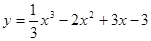 ;
; ; 2.91
; 2.91 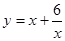 ;
;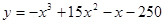 ; 2.93
; 2.93 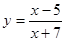 ;
;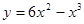 ; 2.95
; 2.95 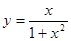 .
. ; 2.97
; 2.97 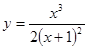 ; 2.98
; 2.98 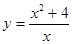 ;
;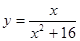 ; 2.100
; 2.100 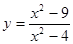 ; 2.101
; 2.101 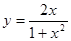 ;
;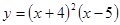 ; 2.103
; 2.103  ; 2.104
; 2.104  .
.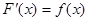 или
или 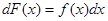 .
.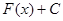 ; где С – постоянная.
; где С – постоянная.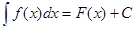
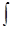 – знак интеграла, f (x) подынтегральная функция,
– знак интеграла, f (x) подынтегральная функция, 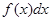 - подынтегральное выражение, х – переменная интегрирования.
- подынтегральное выражение, х – переменная интегрирования.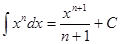 , n ≠ -1,
, n ≠ -1, ,
, ,
, ,
,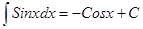 ,
, ,
,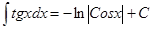 ,
,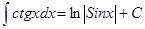 ,
,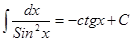 ,
, ,
,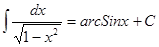 ,
, ,
,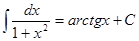 ,
, ,
, ,
,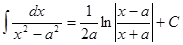 ,
, .
.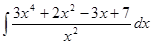 .
.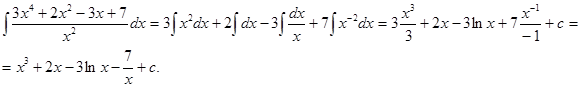
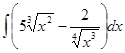 .
.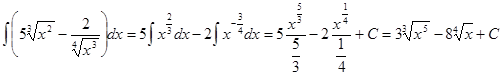 .
.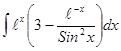 .
.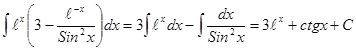 .
. . Результат проверить дифференцированием.
. Результат проверить дифференцированием. .
. .
.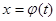 , где
, где 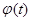 - монотонная, непрерывная дифференцируемая функция новой переменной t. Формула замены переменной в этом случае имеет вид
- монотонная, непрерывная дифференцируемая функция новой переменной t. Формула замены переменной в этом случае имеет вид ;
;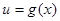 , где u – новая переменная.
, где u – новая переменная.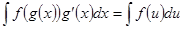
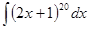 .
.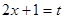 . Найдем дифференциал от обеих частей подстановки:
. Найдем дифференциал от обеих частей подстановки: 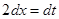 , откуда
, откуда 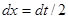 . Следовательно,
. Следовательно, .
.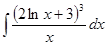 .
.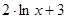 равна
равна 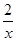 , применим подстановку
, применим подстановку 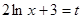 . Дифференциал от обеих частей равен
. Дифференциал от обеих частей равен 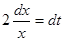 ,
, 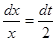 .
.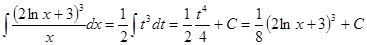 .
. .
.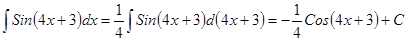 .
.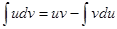 ;
;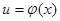 ,
, 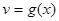 - непрерывно дифференцируемые функции от х. С помощью этой формулы нахождение интеграла
- непрерывно дифференцируемые функции от х. С помощью этой формулы нахождение интеграла  сводится к отысканию другого интеграла
сводится к отысканию другого интеграла 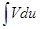 , ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
, ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.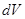 - та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
- та часть подынтегрального выражения, интеграл от которой известен или может быть найден.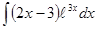 .
. ,
, 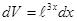 , тогда
, тогда 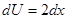
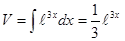 . Следовательно,
. Следовательно,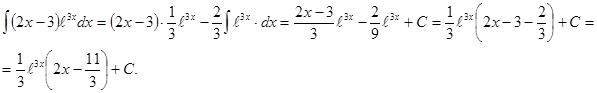
 .
.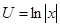 ,
, 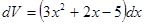 , тогда
, тогда 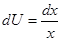 ,
, 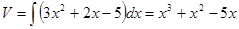 . Следовательно,
. Следовательно,
 .
.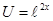 ,
,  , тогда
, тогда 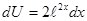 ,
, 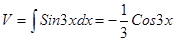 . Следовательно,
. Следовательно,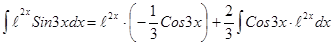 .
. , тогда
, тогда 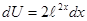 ,
, 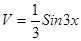 .
.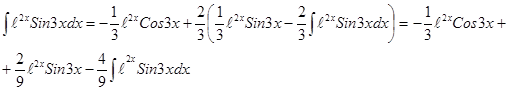
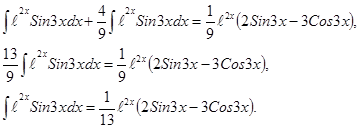
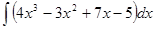 ; 3.2
; 3.2  ;
; ; 3.4
; 3.4 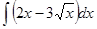 ;
;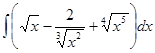 ; 3.6
; 3.6 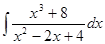 ;
;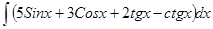 ; 3.8
; 3.8 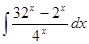 ;
; ; 3.10
; 3.10  ;
;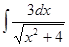 ; 3.12
; 3.12 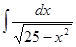 ;
;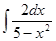 ; 3.14
; 3.14 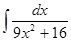 ;
;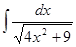 ; 3.16
; 3.16 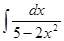 ;
;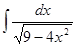 ; 3.18
; 3.18 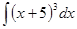 ;
; ; 3.20
; 3.20 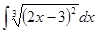 ;
;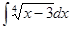 ; 3.22
; 3.22 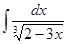 ;
; ; 3.24
; 3.24 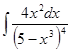 ;
; ; 3.26
; 3.26  ;
; ; 3.28
; 3.28  ;
;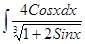 ; 3.30
; 3.30 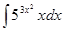 ;
; ; 3.32
; 3.32 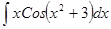 ;
;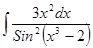 ; 3.34
; 3.34 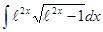 ;
; ; 3.36
; 3.36  ;
; ; 3.38.
; 3.38. 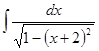 ;
;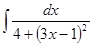 ; 3.40
; 3.40 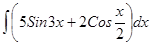 ;
;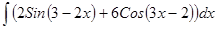 ; 3.42
; 3.42 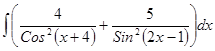 ;
; ; 3.44
; 3.44 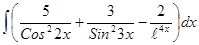 ;
; ; 3.46
; 3.46 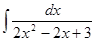 ;
;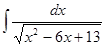 ; 3.48
; 3.48 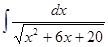 ;
;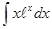 ; 3.50
; 3.50  ;
;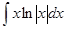 ; 3.52
; 3.52 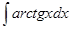 ;
;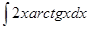 ; 3.54
; 3.54 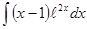 ;
; ; 3.56
; 3.56 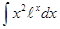 ;
;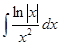 ; 3.58
; 3.58 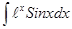 ;
; ; 3.60
; 3.60 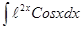 ;
;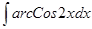 .
.

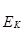 .
.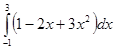 ; 4.2
; 4.2  ; 4.3
; 4.3 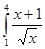 ;
;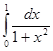 ; 4.5
; 4.5 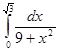 ; 4.6
; 4.6 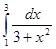 ;
;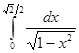 ; 4.8
; 4.8 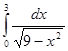 ; 4.9
; 4.9 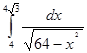 ;
;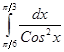 ; 4.11
; 4.11  ; 4.12
; 4.12 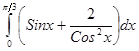 ;
;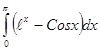 4.14
4.14  ; 4.15
; 4.15 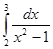 ;
; ; 4.17
; 4.17 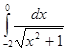 ; 4.18
; 4.18 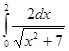 ;
;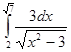 ; 4.20
; 4.20  ; 4.21
; 4.21 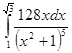 ;
;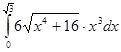 ; 4.23
; 4.23 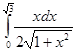 ; 4.24
; 4.24 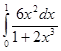 ;
;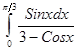 ; 4.26
; 4.26 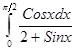 ; 4.27
; 4.27  ;
; ; 4.29
; 4.29 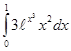 ; 4.30
; 4.30 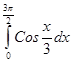 ;
;


