
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выпуклость, вогнутость. Точки перегиба.Содержание книги
Поиск на нашем сайте
График функции  называется выпуклым в интервале (a, b), если он расположен ниже касательной, проведенной в любой точке этого интервала (рис.3). называется выпуклым в интервале (a, b), если он расположен ниже касательной, проведенной в любой точке этого интервала (рис.3).
График функции Достаточное условие выпуклости (вогнутость) графика функции: если Точка
Пример 9 Найти промежутки выпуклости и вогнутости графика функции
Определим первую и вторую производную
Если Если Кривая выпукла в промежутке Схема исследования функции с помощью производных и построение графика. 1) Найти область определения функции. 2) Исследовать функцию на четность и нечетность. 3) Найти точки пересечения графика функции с осями координат. 4) Исследовать функцию на непрерывность; найти точки разрыва. 5) Найти интервалы возрастания и убывания функции и ее экстремумы. 6) Найти интервалы выпуклости и вогнутости кривой и точки ее перегиба. 7) Построить график.
Пример 10 Построить график функции 1) Область определения функции вся числовая ось, за исключением точки D (у) = (-∞; 0) V(0; +∞). 2) Функция не является ни четной, ни нечетной. 3) Найдем точки пересечения графика с осью 0x, имеем
С осью 0у функция не пересекается. 4) Точка разрыва 5) Найдем экстремумы функции и интервалы возрастания и убывания. Имеем
Функция возрастает х = 0, точка максимума, х = 2, точка минимума.
6) Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба.
Если х > 0, При х <0,
График функции всюду вогнут. Точек перегиба прямая не имеет. Используя полученные данные построим график (рис.4).
Упражнения Найти производные функции (2.1-2.43): 2.1 2.3 2.5 2.7 2.9 2.11 2.13 2.15 2.17 2.19 2.21 2.23 2.25 2.27 2.29 2.31 2.33
2.35. 2.37 2.39 2.41 2.43 Найти производные и дифференциалы функций (2.44-2.54): 2.44 2.46 2.48 2.50 2.52 2.54 Найти производные высших порядков (2.55-2.62) 2.55 2.56 2.57 2.58 2.59 2.60 2.61 2.62 Найти интервалы монотонности функций (2.63-2.70): 2.63 2.65 2.67 2.69 Исследовать с помощью первой производной функции на экстремум (2.71-2.78): 2.71 2.73 2.75 2.77 Исследовать с помощью второй производной функции на экстремум (2.79-2.85): 2.79 2.81 2.83 2.85 Найти точки перегиба и интервалы выпуклости и вогнутости следующих кривых (2.86-2.95): 2.86 2.88 2.90 2.92 2.94 Исследовать функции и построить их график (2.96-2.104): 2.96 2.99 2.102 Неопределенный интеграл
Функция F(х) называется первообразной для функции f (x), если Если функция f(х) имеет первообразную F(x), то она имеет бесконечное множество первообразных, причем все первообразные содержатся в выражении Неопределенным интегралом от функции f (x) называется совокупность всех ее первообразных.
Отыскание неопределенного интеграла называется интегрированием. Свойства неопределенного интеграла. 1) 2) 3) 4) 5) Основные интегралы. 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17) Методы интегрирования I. Непосредственное интегрирование: подынтегральное выражение путем преобразований и использования свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам. Пример 1 Вычислить Разделим числитель на знаменатель, получим
Пример 2 Найти Приведем подынтегральные выражения к степенным
Пример 3 Найти Раскроем скобки
Пример 4 Найти Преобразуем знаменатель
Проверим результат
Получили подынтегральную функцию, интеграл найден верно.
II. Замена переменной в неопределенном интеграле: замена переменной в неопределенном интеграле производится с помощью подстановок двух видов:
1)
2) Формула замены переменной при такой постановке:
Пример 5 Найти Приведем подынтегральное выражение к табличному с помощью замены
Пример 6 Найти Так как производная выражения
Пример 7 Найти Во многих случаях нет необходимости записывать, какое выражение мы принимаем за новую переменную.
III. Интегрирование по частям: интегрированием по частям называется нахождение интеграла по формуле
где При этом за U берется такая функция, которая при дифференцировании упрощается, а за Пример 8 Найти Положим
Пример 9 Найти Положим
Пример 10 Найти Положим
Вновь применим формулу интегрирования по частям. Положим Таким образом,
Так как в правой части стоит искомый интеграл, то перенесем его в левую часть получим
Упражнения Найти интегралы (3.1-3.61): 3.1 3.3 3.5 3.7 3.9 3.11 3.13 3.15 3.17 3.19 3.21 3.23 3.25 3.27 3.29 3.31 3.33 3.35 3.37 3.39 3.41 3.43 3.45 3.47 3.49 3.51 3.53 3.55 3.57 3.59 3.61
Определенный интеграл
Определенным интегралом от функции
Если функция Числа a и b называют нижним и верхним пределами интегрирования.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.251.175 (0.01 с.) |


 в интервале (a, b), то график функции является выпуклым в этом интервале; если
в интервале (a, b), то график функции является выпуклым в этом интервале; если  , то на этом интервале, график функции – выгнутый.
, то на этом интервале, график функции – выгнутый. графика функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба (рис.3).
графика функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба (рис.3). .
. ,
, .
. , то
, то  .
. , то
, то  .
. и вогнута в промежутке
и вогнута в промежутке  .
.

 ,
,  .
. .
. ,
,  ,
, ,
, .
. ,
, 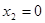 критические точки,
критические точки,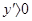 на промежутках
на промежутках  ,
, на промежутке (0; 2).
на промежутке (0; 2).

 >0
>0
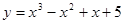 ; 2.2
; 2.2 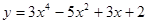 ;
;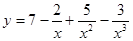 ; 2.4
; 2.4  ;
;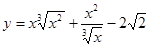 ; 2.6
; 2.6 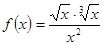 ;
;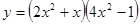 ; 2.8
; 2.8 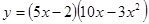 ;
;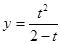 ; 2.10
; 2.10 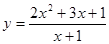 ;
; ; 2.12
; 2.12 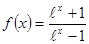 Найти
Найти  ;
;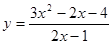 ; 2.14
; 2.14 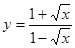 ;
;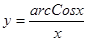 ; 2.16
; 2.16 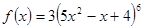 ;
;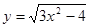 ; 2.18
; 2.18 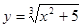 ;
;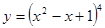 ; 2.20
; 2.20 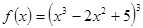 Найти
Найти 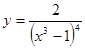 ; 2.22
; 2.22 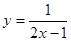 ;
;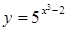 ; 2.24
; 2.24 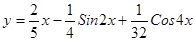 ;
;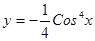 ; 2.26
; 2.26  ;
;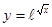 ; 2.28
; 2.28  ;
;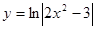 ; 2.30
; 2.30 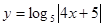 ;
;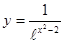 ; 2.32
; 2.32  Найти
Найти  ;
;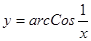 ; 2.34
; 2.34  Найти
Найти 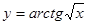 ; 2.36
; 2.36 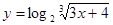 ;
;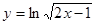 ; 2.38
; 2.38 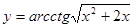 ;
;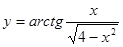 ; 2.40
; 2.40 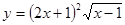 ;
; ; 2.42
; 2.42 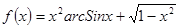 ;
; .
.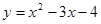 ; 2.45
; 2.45  ;
;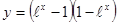 ; 2.47
; 2.47 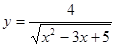 ;
; ; 2.49
; 2.49 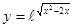 ;
;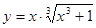 ; 2.51
; 2.51  ;
;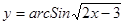 ; 2.53
; 2.53  ;
; .
.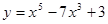 Найти
Найти 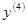 .
.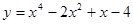 Найти
Найти 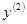 .
.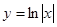 Найти
Найти 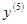 .
.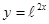 Найти
Найти 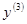 .
.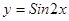 Найти
Найти 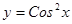 Найти
Найти 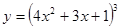 Найти.
Найти. 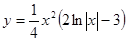 Найти.
Найти.  ; 2.64
; 2.64  ;
; ; 2.66
; 2.66 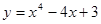 ;
; ; 2.68
; 2.68 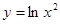 ;
;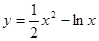 ; 2.70
; 2.70 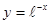 .
.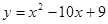 ; 2.72
; 2.72 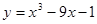 ;
; ; 2.74
; 2.74  ;
;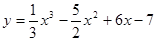 ; 2.76
; 2.76  ;
; ; 2.78
; 2.78  .
.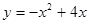 ; 2.80
; 2.80 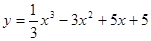 ;
;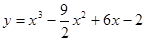 ; 2.82
; 2.82 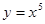 ;
;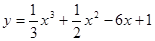 ; 2.84
; 2.84 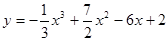 ;
; .
.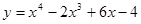 ;
;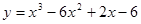 ; 2.89
; 2.89 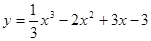 ;
; ; 2.91
; 2.91 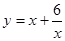 ;
;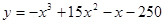 ; 2.93
; 2.93 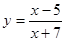 ;
;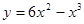 ; 2.95
; 2.95 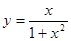 .
. ; 2.97
; 2.97 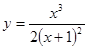 ; 2.98
; 2.98 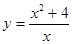 ;
;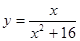 ; 2.100
; 2.100 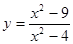 ; 2.101
; 2.101 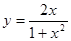 ;
;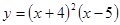 ; 2.103
; 2.103  ; 2.104
; 2.104  .
.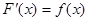 или
или 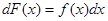 .
.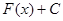 ; где С – постоянная.
; где С – постоянная.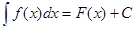
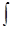 – знак интеграла, f (x) подынтегральная функция,
– знак интеграла, f (x) подынтегральная функция, 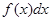 - подынтегральное выражение, х – переменная интегрирования.
- подынтегральное выражение, х – переменная интегрирования. ,
, ,
, ,
, , где а – постоянная,
, где а – постоянная, .
.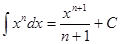 , n ≠ -1,
, n ≠ -1, ,
, ,
, ,
,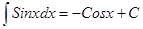 ,
, ,
,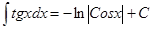 ,
,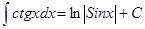 ,
,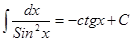 ,
, ,
,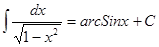 ,
, ,
,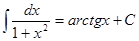 ,
, ,
, ,
,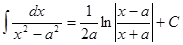 ,
, .
.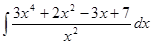 .
.
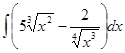 .
.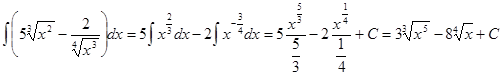 .
.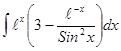 .
.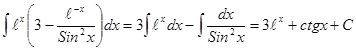 .
. . Результат проверить дифференцированием.
. Результат проверить дифференцированием. .
. .
.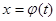 , где
, где  - монотонная, непрерывная дифференцируемая функция новой переменной t. Формула замены переменной в этом случае имеет вид
- монотонная, непрерывная дифференцируемая функция новой переменной t. Формула замены переменной в этом случае имеет вид ;
;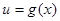 , где u – новая переменная.
, где u – новая переменная.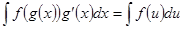
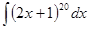 .
.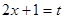 . Найдем дифференциал от обеих частей подстановки:
. Найдем дифференциал от обеих частей подстановки: 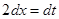 , откуда
, откуда 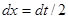 . Следовательно,
. Следовательно, .
.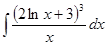 .
.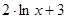 равна
равна 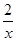 , применим подстановку
, применим подстановку 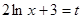 . Дифференциал от обеих частей равен
. Дифференциал от обеих частей равен 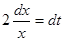 ,
, 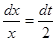 .
.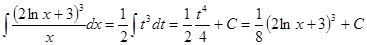 .
. .
.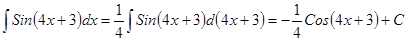 .
.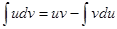 ;
;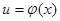 ,
, 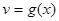 - непрерывно дифференцируемые функции от х. С помощью этой формулы нахождение интеграла
- непрерывно дифференцируемые функции от х. С помощью этой формулы нахождение интеграла  сводится к отысканию другого интеграла
сводится к отысканию другого интеграла 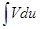 , ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
, ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.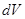 - та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
- та часть подынтегрального выражения, интеграл от которой известен или может быть найден.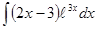 .
. ,
, 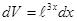 , тогда
, тогда 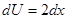
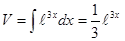 . Следовательно,
. Следовательно,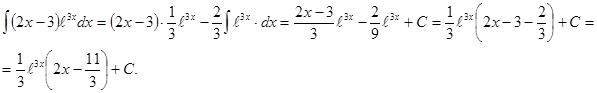
 .
.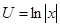 ,
, 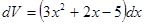 , тогда
, тогда 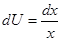 ,
, 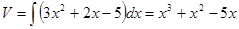 . Следовательно,
. Следовательно,
 .
.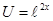 ,
,  , тогда
, тогда 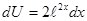 ,
, 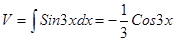 . Следовательно,
. Следовательно,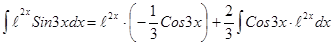 .
. , тогда
, тогда 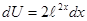 ,
, 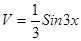 .
.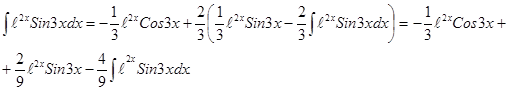
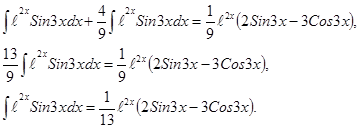
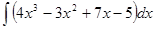 ; 3.2
; 3.2  ;
; ; 3.4
; 3.4 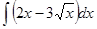 ;
;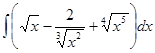 ; 3.6
; 3.6 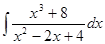 ;
;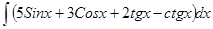 ; 3.8
; 3.8 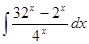 ;
; ; 3.10
; 3.10  ;
;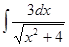 ; 3.12
; 3.12 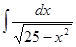 ;
;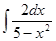 ; 3.14
; 3.14 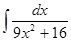 ;
;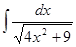 ; 3.16
; 3.16 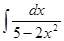 ;
;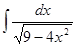 ; 3.18
; 3.18 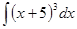 ;
; ; 3.20
; 3.20 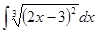 ;
;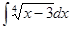 ; 3.22
; 3.22 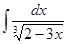 ;
; ; 3.24
; 3.24 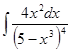 ;
; ; 3.26
; 3.26  ;
; ; 3.28
; 3.28  ;
;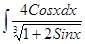 ; 3.30
; 3.30 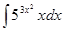 ;
; ; 3.32
; 3.32 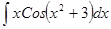 ;
;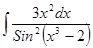 ; 3.34
; 3.34 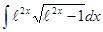 ;
; ; 3.36
; 3.36  ;
; ; 3.38.
; 3.38. 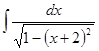 ;
;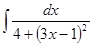 ; 3.40
; 3.40 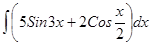 ;
;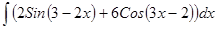 ; 3.42
; 3.42 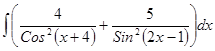 ;
; ; 3.44
; 3.44 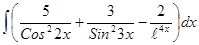 ;
; ; 3.46
; 3.46 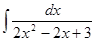 ;
;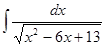 ; 3.48
; 3.48 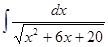 ;
;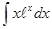 ; 3.50
; 3.50  ;
;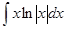 ; 3.52
; 3.52 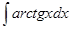 ;
;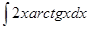 ; 3.54
; 3.54 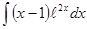 ;
; ; 3.56
; 3.56 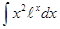 ;
;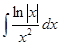 ; 3.58
; 3.58 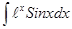 ;
; ; 3.60
; 3.60 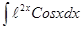 ;
;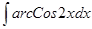 .
. на отрезке [a; b] (или в пределах от a до b) называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков (max Δxк) стремится к нулю:
на отрезке [a; b] (или в пределах от a до b) называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков (max Δxк) стремится к нулю:

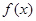 непрерывна на [a; b], то предел интегральной суммы существует и не зависит от способа разбиения отрезка [a; b] на элементарные отрезки и от выбора точек
непрерывна на [a; b], то предел интегральной суммы существует и не зависит от способа разбиения отрезка [a; b] на элементарные отрезки и от выбора точек 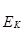 .
.


