
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 15 Простейшие рациональные и их интегрированиеСодержание книги
Поиск на нашем сайте Как мы увидим ниже, далеко не всякая элементарная функция имеет интеграл, выражающийся в элементарных функциях. Поэтому очень важно выделить такие классы функций, интегралы которых выражаются через элементарные функции. Простейшим из этих классов является класс рациональных функций. Всякую рациональную функцию можно представить в виде рациональной дроби, т. е. в виде отношения двух многочленов:
здесь М(х)-многочлен, а Пример. Пусть дана неправильная рациональная дробь
Разделив числитель на знаменатель (по правилу деления многочленов), получим
Так как интегрирование многочленов не представляет затруднений, то основная трудность при интегрировании рациональных дробей заключается в интегрировании правильных рациональных дробей. Определение. Правильные рациональные дроби вида (1). (2). (3) (4) Интегрирование простейших дробей типа (1),(2) и (3) не составляет большой трудности, поэтому мы приведем их интегрирование без каких-либо дополнительных пояснений: (1) (2) (3) = Более сложных вычислений требует интегрирование простейших дробей (4) типа. Пусть нам дан интеграл такого типа: (4) Произведем преобразования:
Первый интеграл берется подстановкой
Второй интеграл- обозначим его через Ik-запишем в виде
полагая
(по предположению корни знаменателя комплексные, а следовательно,
Преобразуем интеграл:
Интегрируя по частям,будем иметь
Подставляя это выражение в равенство (1), получим
= = В правой части содержится интеграл того же типа, что
Подставляя затем всюду вместо t и m их значения, получим выражение интеграла (4) через х и заданные числа А, B, p,q.
Вопрос 16 Разложение правильной дроби на простейшие Целой функцией называется многочлен (полином). Определение 2. Дробно-рациональной функцией называется дробь, числителем и знаменателем которой являются многочлены.
Определение 3. Дробно-рациональная функция называется неправильной рациональной дробью, если степень числителя не меньше степени знаменателя(n m). Определение 4. Дробно-рациональная функция называется правильной, если степень числителя меньше степени знаменателя. Теорема:
Простейшие рациональные дроби. 1) 2) 3) Выделяем полный квадрат и делаем замену переменной:
Делаем обратную замену переменной и получаем окончательный ответ.
Вопрос 17 Интегрирование рациональных дробей Вид простейших дробей определяется корнями знаменателя f(x). Здесь возможны следующие случаи. 1.Случай. Корни знаменателя действительны и различны, т. е. F(x)=(x-a)(x-b)…(x-d). В этом случае дробь
и тогда
2. Случай. Корни знаменателя действительные, причем некоторые из них кратные:
В этом случае дробь Пример 1.
3. Случай. Среди корней знаменателя есть комплексные неповторяющиеся(т.е. различные):
В этом случае дробь Пример 2.Требуется вычислить интеграл
Следовательно,
Полагая х=1, получим 1=2С, С= Ѕ; полагая х=0, получим 0= -B+C, B=1/2. Приравнивая коэффициенты при
4. Случай. Среди корней знаменателя есть комплексные кратные:
В этом случае разложение дроби Пример 3. Требуется вычислить интеграл
Решение. Разлагаем дробь на простейшие:
откуда
Комбинируя указанные выше методы определения коэффициентов, находим А=1, В= - 1, С=0, D=0, Е=1. Таким образом, получаем
Из всего изложенного следует, что интеграл от любой рациональной функции может быть выражен через элементарные функции в конечном виде, а именно: 1) через логарифмы- в случаях простейших дробей 1 типа; 2) через рациональные функции- в случае простейших дробей 2 типа 3) через логарифмы и арктангенсы- в случае простейших дробей 3 типа 4) через рациональные функции и арктангенсы- в случае простейших дробей 4 типа. Вопрос 18 Универсальная тригонометрическая подстановка.
В то же время функция Теорема. Интеграл вида
В результате проведенных преобразований
Подстановка
называется универсальной тригонометрической подстановкой.
Интегралы вида
находятся с помощью тригонометрических формул
20.Вычисление интегралов вида В этом случае полезно пользоваться следующими правилами: А) если m - нечетное положительное число, то вносим
Б) если оба показателя m и n - четные положительные числа, то подынтегральную функцию преобразуют с помощью формул понижения степени:
В) если число m+n является четным отрицательным числом, то можно сделать замену переменной
Г) если степени m и n отрицательны, то часто бывает полезным уменьшить степени с помощью основного тригонометрического тождества. Смотрипример 7.
Примечание. В общем случае интегралы вида
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 645; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.007 с.) |

 Не ограничивая общности рассуждения, будем предполагать, что эти многочлены не имеют общих корней. Если степень числителя ниже степени знаменателя, то дробь называется правильной, в противном случае дробь называется неправильной. Если дробь неправильная, то, разделив числитель на знаменатель (по правилу деления многочленов), можно представить данную дробь в виде суммы многочлена и некоторой правильной дроби:
Не ограничивая общности рассуждения, будем предполагать, что эти многочлены не имеют общих корней. Если степень числителя ниже степени знаменателя, то дробь называется правильной, в противном случае дробь называется неправильной. Если дробь неправильная, то, разделив числитель на знаменатель (по правилу деления многочленов), можно представить данную дробь в виде суммы многочлена и некоторой правильной дроби: ;
;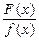 - правильная дробь.
- правильная дробь.
 .
.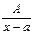
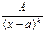 (k-целое положительное число
(k-целое положительное число 
 (корни знаменателя комплексные, т.е.
(корни знаменателя комплексные, т.е. 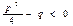 ).
). (k-целое положительное число
(k-целое положительное число 



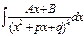
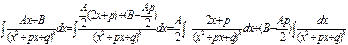
 :
:
 ,
,
 ). Далее поступаем следующим образом:
). Далее поступаем следующим образом: .
.
 .
.
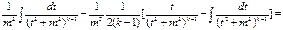
 .
. , но показатель степени знаменателя подынтегральной функции на единицу ниже
, но показатель степени знаменателя подынтегральной функции на единицу ниже 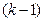 ;таким образом, мы выразили
;таким образом, мы выразили  Продолжая идти тем же путем, дойдем до известного интеграла:
Продолжая идти тем же путем, дойдем до известного интеграла:


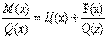
 - задача свелась к интегрированию правильной рациональной дроби.
- задача свелась к интегрированию правильной рациональной дроби.
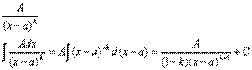

 Тогда интеграл примет вид:
Тогда интеграл примет вид: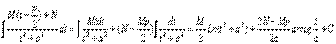
 Теорема 1. Если знаменатель Q(x) имеет любые корни, то правильная дробь разлагается на сумму простейших дробей 1 и 2 типа.
Теорема 1. Если знаменатель Q(x) имеет любые корни, то правильная дробь разлагается на сумму простейших дробей 1 и 2 типа.  (1) Интегрирование правильной рациональной дроби.
(1) Интегрирование правильной рациональной дроби. сумме интегралов от простейших дробей
сумме интегралов от простейших дробей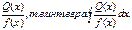 Если данная дробь неправильная, то мы представляем ее в виде суммы многочлена M(x) и правильной рациональной дроби
Если данная дробь неправильная, то мы представляем ее в виде суммы многочлена M(x) и правильной рациональной дроби 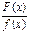 . Последнюю же представляем по формуле в виде суммы простейших дробей. Таким образом, интегрирование всякой рациональной дроби сводится к интегрированию многочлена и нескольких простейших дробей.
. Последнюю же представляем по формуле в виде суммы простейших дробей. Таким образом, интегрирование всякой рациональной дроби сводится к интегрированию многочлена и нескольких простейших дробей. разлагается на простейшие дроби 1типа:
разлагается на простейшие дроби 1типа:
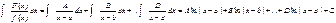

 разлагается на простейшие дроби 1и 2 типов.
разлагается на простейшие дроби 1и 2 типов.

 .Разложим подынтегральную дробь на простейшие:
.Разложим подынтегральную дробь на простейшие: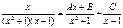
 .
.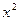 , получим 0=А+С, откуда А= - Ѕ. Таким образом,
, получим 0=А+С, откуда А= - Ѕ. Таким образом,
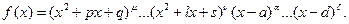
 .
.


 . Например,
. Например, ,
, 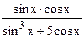 ,
,  .
. рациональной не является.
рациональной не является. с помощью подстановки
с помощью подстановки  преобразуется в интеграл от рациональной дроби.Для доказательства выразим
преобразуется в интеграл от рациональной дроби.Для доказательства выразим 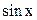 ,
,  и
и  через
через  :
:


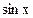 ,
,  и
и 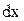 превратились в рациональные дроби от
превратились в рациональные дроби от 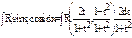 В данном выражении рациональные дроби подставлены в рациональную функцию. Так как над ними выполняются лишь арифметические операции, то в результате получается также рациональная дробь. Итак, рациональную функцию от тригонометрических функций можно проинтегрировать, превратив ее в рациональную дробь.
В данном выражении рациональные дроби подставлены в рациональную функцию. Так как над ними выполняются лишь арифметические операции, то в результате получается также рациональная дробь. Итак, рациональную функцию от тригонометрических функций можно проинтегрировать, превратив ее в рациональную дробь. ,
,  ,
,  ,
, 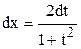
 )
)


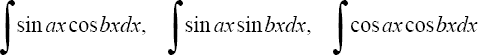
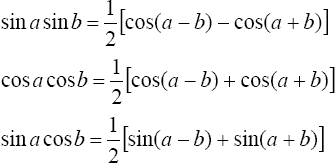
 , где m и n? целые числа.
, где m и n? целые числа. под знак дифференциала или, (что то же самое) делаем замену переменной
под знак дифференциала или, (что то же самое) делаем замену переменной  . При этом число n может быть рациональной дробью. Аналогично, если n - нечетное положительное число, то вносим под знак дифференциала
. При этом число n может быть рациональной дробью. Аналогично, если n - нечетное положительное число, то вносим под знак дифференциала  или применяем подстановку
или применяем подстановку  . Сравни с 1. Смотри
. Сравни с 1. Смотри ,
,  и
и  .
. или
или 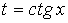 . Смотри пример 6.
. Смотри пример 6.


