
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция нескольких переменных.Содержание книги
Поиск на нашем сайте Функция нескольких переменных. Функцией переменных на множестве стве ствами D и Y, при котором для любой точки
Множество D называется областью определения функции (ООФ), Y — областью значений функции. Так, функция двух переменных
Частное и полное приращение Пусть дана Z=f(x,y) которая определена в области Д Придадим переменной х приращение?ха переменную у оставим без изменения. Часным приращением фун Z=f(x,y) по переменной х называют величина?хz которая определяется соотношением?хz =f(x+?х,y)- f(x,y). Аналогично определяется часное приращение функции по переменной «у».?уz =f(x,?у+y)-f(x,y) Полным приращением функции Z=f(x,y) наз величина?Z которая определяется сотношением?z =f(x+?х,?у+y)-f(x,y) Предел и непрерывность функции двух независимых переменных Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается (не выполняется хотя бы одно из условий непрерывности функции в точке), называются точками разрыва этой функции. Точки разрыва z=ƒ(х;у) могут образовывать целые линии разрыва. Так, функция Можно дать другое, равносильное приведенному выше, определение непрерывности функции z=ƒ(х;у) в точке. Обозначим Δх=х—х0, Δу=у—у0, Δz=ƒ(х;у)—ƒ(х0;у0). Величины Δх и Δу называются приращениями аргументов х и у, а Δz — полным приращением функции ƒ(х;у) в точке М0(х0;у0). Функция z = ƒ(х;у) называется непрерывной в точке М0(х0;у0) є D, если выполняется равенство Пользуясь определением непрерывности и теоремами о пределах, можно доказать, что арифметические операции над непрерывными функциями и построение сложной функции из непрерывных функций приводит к непрерывным функциям — подобные теоремы имели место для функций одной переменной Частные производные. Функции двух переменных. Частная производная функции нескольких переменных — это производная относительно одной переменной, все другие переменные при нахождении считаются константами. Для упрощения ограничимся случаем функций от трех переменных; все дальнейшее, однако, справедливо и для функций любого числа переменных. Пусть в некоторой области D имеем функцию Аналогично определяются и частные производные функции Градиент функции трех переменных. Градиентом функции трех переменных u = f (x, y, z) в точке A = (x0, y0, z0)
называется вектор, координаты которого равны частным производным функции в этой точке:
∂u ∂u ∂u grad u = ; ; . ∂x A ∂y A ∂z A
В направлении градиента функция имеет наибольший рост. Интегралы вида
находятся с помощью тригонометрических формул
20.Вычисление интегралов вида В этом случае полезно пользоваться следующими правилами: А) если m - нечетное положительное число, то вносим
Б) если оба показателя m и n - четные положительные числа, то подынтегральную функцию преобразуют с помощью формул понижения степени:
В) если число m+n является четным отрицательным числом, то можно сделать замену переменной
Г) если степени m и n отрицательны, то часто бывает полезным уменьшить степени с помощью основного тригонометрического тождества. Смотрипример 7.
Примечание. В общем случае интегралы вида
Понятие интегральной суммы Понятие интегральной суммы естественно обобщается на случай знакопеременной функции. 25 Свойства определенного интеграла 1) Если f (x) = c = const, то 3) Если f1 (x) и f2 (x) интегрируемые на [a; b], то: 4) Если в определенном интеграле поменять местами пределы интегрирования, то интеграл только изменит свой знак на противоположный. 5) Определенный интеграл с одинаковыми пределами интегрирования равен нулю. 6) Если f (x) - интегрируема в любом из промежутков [a; b], [a; c], [c; b], то: 8) Если f (x), g (x) - интегрируемые и f (x) ³ g (x) для x Î [a; b], b> a, то: 9) Если f (x) - интегрируема и m £ f (x) £ M, для x Î [a; b], b> a, то 10) (Теорема о среднем): Если ф-ия f (x) - непрерывная для x Î [a; b], b> a, то найдется такая точка x = c Î [a; b], что: Есть в тетради. Есть в тетради. Комплексная плоскость
Рассмотрим декартову систему координат x0y. Пусть каждому числу z = a + bi ставится в соответствие точка z (a; b). Такую плоскость назовем комплексной. Иными словами с каждой точкой z этой плоскости связывают радиус-вектор, определяющий положение данной точки. Угол между положительным направлением оси 0х и радиус-вектором, отсчитанным в направлении против часовой стрелки, называется аргументом. Ось 0х называется действительной осью комплексной плоскости. Ось 0y называется мнимой осью комплексной плоскости. Аргумент может принимать значения из интервала -∞ < arg z < ∞. Наименьшее по модулю значение аргумента называется главным и обозначается arg z = φ. Из рисунка следует, что:
Чтобы найти аргумент, необходимо учитывать, в какой четверти комплексной плоскости находится число: I квадрант φ1 = arg z1 = φ; II квадрант φ1 = arg z1 = π - φ; III квадрант φ1 = arg z1 = π + φ; IV квадрант φ1 = arg z1 = 2π - φ;. Найдем модуль и аргумент комплексного числа:
Арифметические действия над комплексными числами Сумма коммутативности: z1 + z2 = z2 + z1 ассоциативности: (z1 + z2) + z3 = z1 + (z2 + z3) Произведение коммутативности: z1 * z2 = z2 * z1 ассоциативности: (z1 * z2) * z3 = z1 * (z2 * z3) дистрибутивности: z1 * (z2 + z3) = z1 * z2 + z1 * z3 Разность Частное Первого порядка. Уравнение вида
F(x, y, y/) = 0 (1.4) называется уравнением первого порядка. В простейших случаях оно может быть разрешено относительно у/=f(x,y). (1.4’) Общее решение (1.4) имеет вид у=j(х,С), (1.5) где С - константа. Геометрически общее решение представляет собой семейство интегральных кривых.
Интегральные кривые обладают тем свойством, что все касательные в точке М(х,у) имеют наклон tga = f ’(x,y). Если задать точку М0(х0,у0), через которую должна проходить интегральная кривая, то это требование называется начальным условием y = у0, х = х0 и тогда у0 = j(х0,С0). Определяется С - константа; в результате получаем частное интегральное решение у = j(х,С0). В этом состоит задача Коши. Задача Коши. Найти решение у = j(х) дифференциального уравнения (1.4’), удовлетворяющее начальному условию: у0=j(х0) Уравнение второго порядка Однородное уравнение второго порядка: a2y'' + a1y' + a0y = 0 интегрируется следующим образом: Пусть λ1,λ2 — корни характеристического уравнения. a2λ2 + a1λ + a0 = 0, Числовые ряды. Определение ряда и его сходимостьВ настоящей главе обобщим понятие суммы на некоторые случаи бесконечного числа слагаемых и изучим свойства таких сумм. Определение 1. Пусть задана последовательность чисел. а1, а2, а3,..., аn,... (1.1) Выражение вида
называется рядом, а число аn - его n-ным членом, n = 1,2,.... Сразу же заметим, что в нашем случае (1.2) - числовой ряд. Если же последовательность есть последовательность функций, то ряд называется функциональным (аn = fn(x), n = 1,2,...). Примеры. аn = а×qn-1,. Понятно, что изучение функциональных рядов всегда можно свести к изучению числовых рядов, зафиксировав х = х0. Ряд (1.2) считается заданным, если мы знаем его общий член аn (то есть член, стоящий на n-ном месте). Из теории последовательностей мы знаем, что аn выражается как функция номера n. Определение 2. Конечная сумма первых n членов ряда называется n-й частичной суммой, а оставшиеся члены, начиная с n + 1, написанные в том же порядке, что и в данном ряду, называется n-ным остатком ряда.
(1.3) Sn - n-ная частичная сумма (n = 1,2,...,k) Rn = an+1 + an+2 +... + an+i +..., (1.4) Rn - остаток ряда. Определение 3. Ряд Если ряд сходится, то
Если Необходимый признак сходимости ряда. Числовые ряды - выражение типа
(1)
Ряд считается заданным, если задан общий член. Сумма первых n членов ряда называется n-ной суммой членов ряда.
- называют суммой ряда (1) и говорят, что ряд сходится.
Если предел не существует, то ряд (1) считается расходящимся. Свойства рядов: 1) Если ряд (1) сходится, то сходится и ряд. 2) Если ряд (1) сходится и ряд 3) Если к ряду (1) прибавить (или отбросить) конечное число членов, то полученный ряд и ряд (1) сходящиеся и расходящиеся одновременно. Теорема (необходимый признак сходимости числового ряда). Если ряд (1) сходится, то его общий член стремится к нулю, то есть Если не выполняется, то расходится. Достаточное условие расходимости ряда: если предел Необходимый признак сходимости ряда недостаточен для сходимости, поскольку существуют ряды, которые расходятся, но необходимый признак сходимости для них выполняется.
Определение Пусть функция f(x) бесконечно дифференцируема в некоторой окрестности точки a. Формальный ряд называется рядом Тейлора функции f в точке a. Свойства Если f есть аналитическая функция, то её ряд Тейлора в любой точке a области определения f сходится к f в некоторой окрестности a. Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности a. Например, Коши предложил такой пример:
У этой функции все коэффициенты ряда Тейлора равны нулю. Формула Тейлора Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки. Теорема: Þ Пусть функция f(x) имеет n + 1 производную в некоторой окрестности точки a, U(a,ε) Þ Пусть Þ Пусть p — произвольное положительное число, тогда:
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша). функция нескольких переменных. Функцией переменных на множестве стве ствами D и Y, при котором для любой точки
Множество D называется областью определения функции (ООФ), Y — областью значений функции. Так, функция двух переменных
Частное и полное приращение Пусть дана Z=f(x,y) которая определена в области Д Придадим переменной х приращение?ха переменную у оставим без изменения. Часным приращением фун Z=f(x,y) по переменной х называют величина?хz которая определяется соотношением?хz =f(x+?х,y)- f(x,y). Аналогично определяется часное приращение функции по переменной «у».?уz =f(x,?у+y)-f(x,y) Полным приращением функции Z=f(x,y) наз величина?Z которая определяется сотношением?z =f(x+?х,?у+y)-f(x,y)
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 445; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

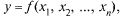 определенной
определенной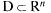 и принимающей значения на множе-
и принимающей значения на множе- называется такое соответствие между множе-
называется такое соответствие между множе- существует единственный элемент
существует единственный элемент 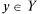
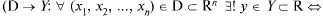

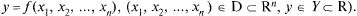

 — множество точек плоскости.
— множество точек плоскости.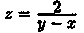 имеет линию разрыва у=х.
имеет линию разрыва у=х. т. е. полное приращение функции в этой точке стремится к нулю, когда приращения ее аргументов х и у стремятся к нулю.
т. е. полное приращение функции в этой точке стремится к нулю, когда приращения ее аргументов х и у стремятся к нулю.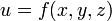 ; возьмем точку
; возьмем точку  в этой области. Если мы будем считать y и z за постоянные значения y 0 и z 0, и будем менять x, то u будет функцией от одной переменной x (в окрестности x 0); можно поставить вопрос о вычислении ее производной в точке
в этой области. Если мы будем считать y и z за постоянные значения y 0 и z 0, и будем менять x, то u будет функцией от одной переменной x (в окрестности x 0); можно поставить вопрос о вычислении ее производной в точке 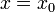 . Придадим этому значению x 0 приращение Δ x, тогда функция получит приращение
. Придадим этому значению x 0 приращение Δ x, тогда функция получит приращение  , которое можно было бы назвать ее частным приращением (по x), поскольку оно вызвано изменением значения лишь одной переменной. По самому определению производной, она представляет собою предел
, которое можно было бы назвать ее частным приращением (по x), поскольку оно вызвано изменением значения лишь одной переменной. По самому определению производной, она представляет собою предел  . Эта производная называется частной производной функции
. Эта производная называется частной производной функции  по x в точке
по x в точке  .
.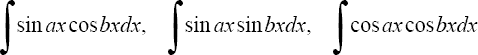
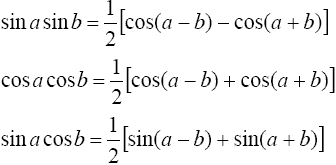
 , где m и n? целые числа.
, где m и n? целые числа. под знак дифференциала или, (что то же самое) делаем замену переменной
под знак дифференциала или, (что то же самое) делаем замену переменной  . При этом число n может быть рациональной дробью. Аналогично, если n - нечетное положительное число, то вносим под знак дифференциала
. При этом число n может быть рациональной дробью. Аналогично, если n - нечетное положительное число, то вносим под знак дифференциала  или применяем подстановку
или применяем подстановку  . Сравни с 1. Смотри
. Сравни с 1. Смотри ,
,  и
и  .
. или
или 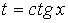 . Смотри пример 6.
. Смотри пример 6.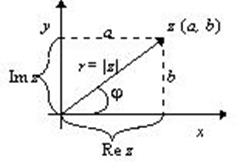
 ,
,  ,
, 


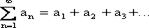 (1.2)
(1.2)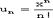
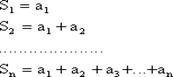
 называется сходящимся, если последовательность его частичных сумм сходится. Если ряд не сходится, то говорят, что он расходится.
называется сходящимся, если последовательность его частичных сумм сходится. Если ряд не сходится, то говорят, что он расходится.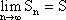 называется его суммой.
называется его суммой. . (1.5)
. (1.5)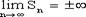 , то
, то 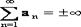 .
.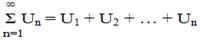
 - члены ряда,
- члены ряда,  - общий член ряда.
- общий член ряда.

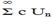 (с - const)
(с - const)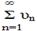 сходится, то
сходится, то  сходится.
сходится.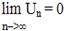 .
. или этот предел не существует, то ряд расходится.
или этот предел не существует, то ряд расходится.

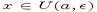
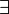 точка
точка 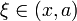 при x < a или
при x < a или  при x > a:
при x > a:



