
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неполные дифференциальные уравнения первого порядкаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Дифференциальное уравнение первого порядка называются неполными, если в нем не содержится (явно) или сама функция у, или независимая переменная х. В том случае, когда правая часть дифференциального уравнения не содержит самой функции у, оно принимает вид:
Отсюда. Таким образом, получено общее решение неполного дифференциального уравнения. Фактически это задача об отыскании первообразной функции (т.е. это непосредственно задача неопределенного интеграла). Во втором случае, т.е. когда дифференциальное уравнение имеет вид, http://www.bgsha.com/ru/learning/images/matematika_yakovenko/3/26.png т.е. в уравнение явно не входит независимая переменная х. Дифференциальное уравнение принимает вид , т.е. получаем у – как независимую переменную, а х – как функцию от у (фактически это обратная функция по отношению к функции у от х). Дифференциальное уравнение второго порядка имеет вид. Определение. Общим решением уравнения второго порядка называется такая функция, Определение. Линейным однородным уравнением второго порядка называется уравнение. Уравнение Определение. Уравнение, которое получается из линейного однородного уравнения заменой функции Известно, что квадратное уравнение Дифференциальные уравнения с разделяющимися переменными Дифференциальное уравнение вида или
называется дифференциальным уравнением с разделяющимися переменными. Заметим, что в данных дифференциальных уравнениях каждая из функций зависит только от одной переменной, т.е. происходит разделение переменных. Для решения такого дифференциального уравнения необходимо домножить или разделить обе части дифференциального уравнения на такое выражение, чтобы в одну часть уравнения входили только функции от
Следует заметить, что при делении обеих частей дифференциального уравнения на выражение, содержащее неизвестные Обратим внимание, что дифференциальные уравнения с разделяющимися переменными легко сводятся к интегрированию.
решение дифференциального уравнения представимо в виде:
где
Однородные дифференциальные уравнения первого порядка Однородным дифференциальным уравнением первого порядка, называется уравнение, имеющее вид
Подстановка
,
,
Замечание. Функция
А функция
.
Поэтому общий вид однородного дифференциального уравнения часто записывают как
,
где - однородная функция нулевой степени однородности.
ТЕОРЕМА.(теорема Коши). Если функция f(х,y) и ее частная производная f'y(х,y) определены и непрерывны в некоторой области G плоскости Оху, то какова бы ни была внутренняя точка (x0,y0) области G, в некоторой окрестности этой точки существует единственное решение уравнения у'=f(x,у), удовлетворяющее условиям: у =у0 при х =х0 (6) Первого порядка. Уравнение вида
F(x, y, y/) = 0 (1.4) называется уравнением первого порядка. В простейших случаях оно может быть разрешено относительно у/=f(x,y). (1.4’) Общее решение (1.4) имеет вид у=j(х,С), (1.5) где С - константа. Геометрически общее решение представляет собой семейство интегральных кривых.
Интегральные кривые обладают тем свойством, что все касательные в точке М(х,у) имеют наклон tga = f ’(x,y). Если задать точку М0(х0,у0), через которую должна проходить интегральная кривая, то это требование называется начальным условием y = у0, х = х0 и тогда у0 = j(х0,С0). Определяется С - константа; в результате получаем частное интегральное решение у = j(х,С0). В этом состоит задача Коши. Задача Коши. Найти решение у = j(х) дифференциального уравнения (1.4’), удовлетворяющее начальному условию: у0=j(х0)
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1915; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.32.53 (0.007 с.) |


 или,
или,  или.
или. 



 которая при любых значениях
которая при любых значениях  и
и  является решением этого уравнения.
является решением этого уравнения. Если коэффициенты
Если коэффициенты  и
и  постоянны, т.е. не зависят от
постоянны, т.е. не зависят от  , то это уравнение называют уравнением с постоянными коэффициентами и записывают его так:.
, то это уравнение называют уравнением с постоянными коэффициентами и записывают его так:. 
 будем называть линейным неоднородным уравнением.
будем называть линейным неоднородным уравнением. единицей, а
единицей, а  и
и  - соответствующими степенями
- соответствующими степенями  , называется характеристическим уравнением.
, называется характеристическим уравнением. имеет решение, зависящее от дискриминанта
имеет решение, зависящее от дискриминанта  :
:  , т.е. если, то корни
, т.е. если, то корни  и
и  - действительные различные числа. Если,
- действительные различные числа. Если,  то
то  . Если же,
. Если же,  т.е.
т.е.  , то
, то  будет мнимым числом, а корни
будет мнимым числом, а корни 


 и
и  , в другую часть уравнения - только функции от
, в другую часть уравнения - только функции от  ,
,  . Затем в полученном дифференциальном уравнении надо проинтегрировать обе части:
. Затем в полученном дифференциальном уравнении надо проинтегрировать обе части:

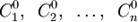 — конкретные числа, то функция вида
— конкретные числа, то функция вида  при всех допустимых значениях параметров (неопределённых констант)
при всех допустимых значениях параметров (неопределённых констант)  называется общим решением дифференциального уравнения.
называется общим решением дифференциального уравнения. (7)
(7) ;
;  ,
,  где
где  преобразует это уравнение к уравнению с разделяющимися переменными.
преобразует это уравнение к уравнению с разделяющимися переменными. 


 называется однородной степени
называется однородной степени  , если
, если  , где
, где  - некоторая константа. Например, функция
- некоторая константа. Например, функция  является однородной функцией степени два, поскольку
является однородной функцией степени два, поскольку является однородной функцией нулевой степени однородности, так как
является однородной функцией нулевой степени однородности, так как






