Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные однородные дифференциальные уравнения сСодержание книги
Поиск на нашем сайте произвольными коэффициентами
Рассмотрим уравнение вида
Определение. Выражение Линейный дифференциальный оператор обладает следующими свойствами: 1) 2) Решения линейного однородного уравнения обладают следующими свойствами: 1) Если функция 2) Если функции Определение. Фундаментальной системой решений линейного однородного дифференциального уравнения n –го порядка на интервале Определение. Если из функций
то этот определитель называется определителем Вронского. Теорема. Если функции Теорема. Если функции Теорема. Для того, чтобы система решений линейного однородного дифференциального уравнения Теорема. Если
где Применение приведенных выше свойств и теорем рассмотрим на примере линейных однородных дифференциальных уравнений второго порядка.
Общее решение линейного однородного дифференциального Уравнения второго порядка
Из вышеизложенного видно, что отыскание общего решения линейного однородного дифференциального уравнения сводится к нахождению его фундаментальной системы решений. Однако, даже для уравнения второго порядка, если коэффициенты р зависят от х, эта задача не может быть решена в общем виде. Тем не менее, если известно одно ненулевое частное решение, то задача может быть решена. Теорема. Если задано уравнение вида
Таким образом, для получения общего решения надо подобрать какое – либо частное решение дифференциального уравнения.
Линейные однородные дифференциальные уравнения с Постоянными коэффициентами
Решение дифференциального уравнения вида Так как При этом многочлен Для того чтобы функция
Так как Как и любое алгебраическое уравнение степени n, характеристическое уравнение В зависимости от коэффициентов k характеристическое уравнение может иметь либо n различных действительных корней, либо среди действительных корней могут быть кратные корни, могут быть комплексно – сопряженные корни, как различные, так и кратные. Сформулируем общее правило нахождения решения линейного однородного дифференциального уравнения с постоянными коэффициентами. 1) Составляем характеристическое уравнение и находим его корни. 2) Находим частные решения дифференциального уравнения, причем: a) каждому действительному корню соответствует решение б) каждому действительному корню кратности m ставится в соответствие m решений:
в) каждой паре комплексно – сопряженных корней
г) каждой паре m – кратных комплексно – сопряженных корней
3) Составляем линейную комбинацию найденных решений. Эта линейная комбинация и будет являться общим решением исходного линейного однородного дифференциального уравнения с постоянными коэффициентами. Пример. Решить уравнение Составим характеристическое уравнение:
Общее решение имеет вид: Пример. Решить уравнение Это линейное однородное дифференциальное уравнение с переменными коэффициентами второго порядка. Для нахождения общего решения необходимо отыскать какое - либо частное решение. Таким частным решением будет являться функция
Преобразуем исходное дифференциальное уравнение к виду:
Общее решение имеет вид: Следовательно,
Окончательно находим: Пример. Решить уравнение Составим характеристическое уравнение:
Общее решение имеет вид: Пример. Решить уравнение Характеристическое уравнение имеет вид: Общее решение имеет вид: Пример. Решить уравнение Характеристическое уравнение имеет вид:
Общее решение имеет вид: Пример. Решить уравнение Характеристическое уравнение имеет вид:
Общее решение имеет вид: Пример. Решить уравнение Характеристическое уравнение имеет вид: Общее решение имеет вид: Пример. Решить уравнение Характеристическое уравнение имеет вид:
Общее решение имеет вид: Пример. Решить уравнение Это уравнение не является линейным, следовательно, приведенный выше метод решения к нему не применим. Понизим порядок уравнения с помощью подстановки Тогда
Окончательно получаем: Это выражение даёт общее решение исходного дифференциального уравнения. Полученное выше решение Пример. Решить уравнение Производим замену переменной:
Общее решение имеет вид:
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.006 с.) |

 .
. называется линейным дифференциальным оператором.
называется линейным дифференциальным оператором.

 является решением уравнения, то функция
является решением уравнения, то функция 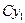 , где С – постоянное число, также является его решением.
, где С – постоянное число, также является его решением. являются решениями уравнения, то
являются решениями уравнения, то  также является его решением.
также является его решением. называется всякая система n линейно независимых на этом интервале решений уравнения.
называется всякая система n линейно независимых на этом интервале решений уравнения.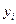 составить определитель n – го порядка
составить определитель n – го порядка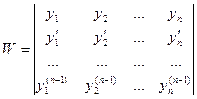 ,
, линейно зависимы, то составленный для них определитель Вронского равен нулю.
линейно зависимы, то составленный для них определитель Вронского равен нулю. ,
, – постоянные коэффициенты.
– постоянные коэффициенты. и известно одно ненулевое решение
и известно одно ненулевое решение  , то общее решение может быть найдено по формуле:
, то общее решение может быть найдено по формуле:
 или, короче, вида
или, короче, вида  будем искать в виде
будем искать в виде  , где k = const.
, где k = const.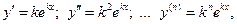 то
то 
 называется характеристическим многочленом дифференциального уравнения.
называется характеристическим многочленом дифференциального уравнения. т.е.
т.е. 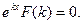
 , то уравнение
, то уравнение  равносильно уравнению
равносильно уравнению  , которое называется характеристическим уравнением.
, которое называется характеристическим уравнением. имеет n корней. Каждому корню характеристического уравнения
имеет n корней. Каждому корню характеристического уравнения  соответствует решение дифференциального уравнения.
соответствует решение дифференциального уравнения. ;
;
 характеристического уравнение ставится в соответствие два решения:
характеристического уравнение ставится в соответствие два решения: и
и  .
.
 .
. Решая которое, находим:
Решая которое, находим:








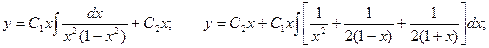

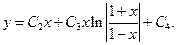

 Следовательно,
Следовательно,
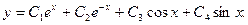

 . Следовательно
. Следовательно 
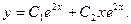

 Следовательно,
Следовательно,



 . Следовательно,
. Следовательно,


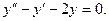
 . Следовательно,
. Следовательно, 
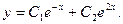

 . Следовательно,
. Следовательно,








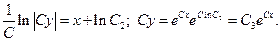

 получается из общего решения при
получается из общего решения при  .
.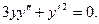
 . Находим
. Находим