
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид y'' + py' +qy = f(x) Для нахождения общего решения этого уравнения нужно найти общее решение у = Рассмотрим один из методов нахождения частного решения – метод неопределенных коэффициентов. Суть метода заключается в следующем: если правая часть уравнения неоднородного уравнения имеет вид f(x)=eαx[Pn(x)cosβx + Qm(x)sinβх], где α и β – действительные числа, а Pn(x) и Qm(x) – многочлены соответственно n - йи m – й степени с действительными коэффициентами, то частное решение у* ищется в виде y* = xl eαx[Ms(x)cosβx+Ns(x)sinβx], где Ms(x) и Ns(x) – многочлены степени s = max(n,m) с неопределенными буквенными коэффициентами, а l – кратность, с которой α + βi входит в число корней характеристического уравнения. Следует отметить, что в общем виде многочлены соответствующей степени, имеют вид: - многочлен 0-ой степени - А - многочлен 1-ой степени - Ах+В - многочлен 2-ой степени - Ах2+Вх+С - многочлен 3-ей степени - Ах3+Вх2+Сх+D и т.д. А, В, С, D, … - неопределенные коэффициенты. Для того, чтобы найти неопределенные коэффициенты, частное решение у*, его производные у*' и у*'' подставляют в левую часть неоднородного уравнения и производят соответствующие упрощения; затем в полученном тождестве приравнивают коэффициенты при подобных членах в левой и правой частях, что дает систему уравнений относительно искомых неопределенных коэффициентов, решив которую находят эти коэффициенты. Замечание. Если правая часть неоднородного уравнения есть сумма функций вида f(x)=f1(x)+f2(x)+ … +fn(x),
нужно предварительно найти частные решения y1*, y2*, …,yn*, соответствующие функциям f1(x, f2(x), …,fn(x). Тогда частное решение данного уравнения запишутся в виде y*= y1*+ y2*+, …,+ yn*.
Более общим методом решения уравнений является метод вариации произвольных постоянных. Пусть у1 и у2 – линейно независимые частные решения однородного уравнения. Тогда общее решение неоднородного уравнения следует искать в виде у=С1(х)у1+С2(х)у2 где функции С1(х) и С2(х) определяются из системы уравнений
Решая эту систему, получим
где Интегрируя С'1(х) и С'2(х) получаем
откуда, подставляя найденные функции в функцию решения, найдем общее решение линейного неоднородного уравнения. Пример 10.12. Найти общее решение дифференциального уравнения y"+4y'=-2xe-4х. Решение. Общее решение неоднородного уравнения равно сумме общего решения у = Найдем общее решение однородного уравнения y"+4y'=0. Составим характеристическое уравнение и решим его k2 + 4k = 0, k1=0, k2=-4. Общее решение однородного уравнения имеет вид
Перейдем к отысканию частного решения у* данного уравнения. Здесь правая часть неоднородного уравнения f(x)=-2xe-4x содержит произведение многочлена первой степени и показательной функции, а также коэффициент в показателе степени совпадает с одни из корней характеристического уравнения, следовательно, необходимо в частное решение добавить множитель х и частное решение будт иметь вид y*= x(Ax+B)e-4x=(Ax2+Bx)e-4x. Вычислим производные функции у* y*'= 2Axe-4x-4e-4x(Ax2+Bx) = (-4Ax2+2Ax-4Bx+B)e-4x y*" = (-8Ax+2A-4B) e-4x-4e-4x(-4Ax2+2Ax -4Bx+B)= = (16Ax2-16Ax +16Bx+2A – 8B)e-4x. Подставим найденные производные в неоднородное уравнение (16Ax2-16Ax +16Bx+2A – 8B)e-4x+4(-4Ax2+2Ax-4Bx+B)e-4x=-2xe-4x (16Ax2-16Ax +16Bx+2A – 8B+16Ax2+8Ax-16Bx+4B)e-4x=-2xe-4x. Приведем подобные члены и сократим равенство на е-4х -8Ax+2A -4B =-2x. Приравняем коэффициенты левой и правой части равенства, стоящие перед х в одинаковой степени, получим систему уравнений, решив которую найдем значения неопределенных коэффициентов А и В:
Получили частное решение неоднородного уравнения y*= Теперь можно записать общее решение данного неоднородного уравнения y = С1 +C2e-4х+ Пример 10.13. Найти общее решение дифференциального уравнения y"+4y=3xcosx. Решение. Общее решение неоднородного уравнения равно сумме общего решения у = Найдем общее решение однородного уравнения y"+4y=0. Составим характеристическое уравнение и решим его k2 + 4 = 0, k1,2=±2i (α=0, β=2) Общее решение однородного уравнения имеет вид
Перейдем к отысканию частного решения у* данного уравнения. Здесь правая часть неоднородного уравнения f(x)=3xcosx содержит произведение многочлена первой степени и тригонометрической функции (α =0, β =1), коэффициенты в правой части неоднородного уравнения не совпадают с корнями характеристического уравнения и частное решение будет иметь вид y*= (Ax+B)cosx+(Cx+D)sinx, где A,B,C,D – неопределенные коэффициенты. Вычислим производные функции у*: y*'=Acosx - (Ax+B)sinx + Csinx + (Cx+D)cosx=(Cx + D + A)cosx + +(-Ax +C - B)sinx y*" =Ccosx - (Cx + D +A)sinx – Asinx+(-Ax+C-B)cosx=(-Ax + 2C – B)cosx + +(-Cx – 2A – D)sinx Подставим найденные производные в неоднородное уравнение, приведем подобные члены и сгруппируем члены при cosx и sinx (3Ax + 3B + 2C)cosx + (3Cx + 3D - 2A)sinx = 3xcosx 3Axcosx + 3Cxsinx + (3B+2C)cosx + (3D-2A)sinx = 3xcosx Приравняем коэффициенты левой и правой части равенства, стоящие перед xcosx, xsinx, cosx и sinx получим систему уравнений, решив которую найдем значения неопределенных коэффициентов A,B,C,D:
Таким образом, частное решение имеет вид y*=xcosx+ Окончательно получаем общее решение неоднородного дифференциального уравнения у = С1cos2x +C2 sin2x+ xcosx+ Задачи контрольной работы В задачах 10.1- 10.20 решить дифференциальные уравнения первого порядка. 10.1. 10.4. 10.7. 10.10. 10.13. 16. 10.19.
В задачах 10.21 – 10.40 найти частное решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям.
10.21. y'' – 7y' + 10y = 0; y(0) = 2; y'(0) = -1. 10.22. y'' + 2y' + 10y = 0; y( 10.23. y'' – 6y' + 9y = 0; y(0) = 1; y' (0) = 0. 10.24. y'' + 8y' + 7y = 0; y(0) = 2; y'(0) = 1. 10.25. y'' + 9y = 0; y(π) = 0; y'(π) = -1. 10.26. y'' – 7y' + 12y = 0; y(0) = 2; у'(0)=-2. 10.27. y'' + 9y' = 0; y(0) = 1; y'(0) = -3. 10.28. y'' – 3y' + 2y = 0; y(0) = 0; y'(0) = 1. 10.29. y'' – 5y' + 6y = 0; y(0) = 5; y'(0) = 0. 10.30. y'' – 2y' + 5y = 0; y(0) = -1; y'(0) = 0. 10.31. y'' + 16y = 0; y(π) = -1; y'(π) = 0. 10.32. y'' + 10y' + 25y = 0; y(0) = 1; y'(0) = 1. 10.33. y'' – 6y' = 0; y(0) = 2; y'(0) = -2. 10.34. y'' – 4y' + 4y = 0; y(0) = 1; y'(0) = 3. 10.35. y'' – 8y' + 15y = 0; y(0) = 1; y'(0) = -2. 10.36. y'' – 4y' + 17y = 0; y( 10.37. y'' – 2y' + y = 0; y(1) = 0; у'(1)=2 10.38. y'' + y = 0; y(π) = -1; y'(π) = -4. 10.39. y'' – 7y' + 6y = 0; y(0) = 2; y'(0) = 0. 10.40. y'' + 8y' + 16y = 0; y(0) = 1; y'(0) = 0.
В задачах 10.41 – 10.60 найти общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами.
10.41. у'' - 2у' = 3х2 + 1 10.51. у'' + 2у' = х2 -3х +1 10.42. у'' - 5у' + 6у = 2хе-х 10.52. у'' - 5у' - 24у = (2х + 3)ех 10.43. у'' + 8у' = (х-1)е2х 10.53. у'' - 2у' - 3у = 8е3х 10.44. у'' - 6у' + 8у = 3е4х 10.54. у'' + 2у' - 3у =- 2е3х 10.45. у'' - 2у' - 3у = хе-х 10.55. у'' + 8у' = (х2+1) е-х 10.46. у'' + у' - 2у = (х = 2)е-2х 10.56. у'' + 4у' + 3у = -хе-х 10.47. у'' + 2у' - 8у = (3х+1)е2х 10.57. у'' - 2у' - 3у =(х + 2)е-х 10.48. у'' + 7у' = 2х2 + х 10.58. у'' + у' + 6у = 2(х – 1)е2х 10.49. у'' - у' = 8х2 ех 10.59. у'' - 4у' = 2х2 – 3х +1 10.50. у'' + 3у' -10у = 2х2ех 10.60. у'' - 5у' + 6у = 2хе3х
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1229; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.007 с.) |

 однородного уравнения, как это было показано в предыдущем параграфе, и какое-либо частное решение у* неоднородного уравнения. Их сумма будет общим решением данного неоднородного уравнения:
однородного уравнения, как это было показано в предыдущем параграфе, и какое-либо частное решение у* неоднородного уравнения. Их сумма будет общим решением данного неоднородного уравнения: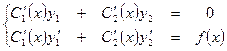
 ,
, 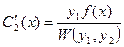
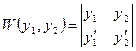
 - определитель Вронского.
- определитель Вронского.
 ,
, однородного уравнения и какого-либо частного решения у* неоднородного уравнения:
однородного уравнения и какого-либо частного решения у* неоднородного уравнения:
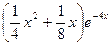
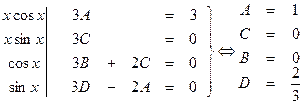
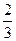 sinx.
sinx. ; 10. 2.
; 10. 2.  ; 10.3.
; 10.3. 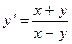 ;
; ; 10. 5.
; 10. 5.  ; 10.6.
; 10.6. 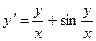 ;
; ; 10.8.
; 10.8.  ; 10.9.
; 10.9. 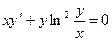 ;
; ; 10.11.
; 10.11. 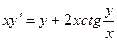 ; 10.12.
; 10.12. 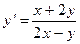 ;
; ; 10.14.
; 10.14. 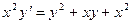 ; 10.15.
; 10.15. 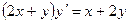 ;
;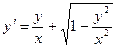 ; 10.17.
; 10.17.  ; 10.18.
; 10.18.  ;
; ; 10.20.
; 10.20.  .
. ) = 0; y'(
) = 0; y'(


