
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Замена переменных в дифференциальных уравнениях первого порядкаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Сведения из теории Сделаем в уравнении
заменой переменной
Примеры решения задач 3.2.1. Решить уравнение ◄ Введем новую неизвестную функцию
3.2.2. Найти решение дифференциального уравнения ◄ Так как
3.3. Задачи для самостоятельного решения Решить уравнения.
Однородные уравнения Сведения из теории Дифференциальное уравнение, которое можно записать в виде
называется однородным. Оно сводится заменой переменной
к уравнению с разделяющимися переменными для функции
Важным примером однородного уравнения является уравнение, правая часть которого – отношение однородных многочленов относительно
Оно приводится к виду, если числитель и знаменатель разделить на
Примеры решения задач 4.2.1. Решить уравнение ◄ Правая часть уравнения – отношение однородных многочленов 2-го порядка. Разделив числитель и знаменатель на – однородное уравнение. Делаем замену
4.2.2. Найти решение дифференциального уравнения ◄ Приведем уравнение к нормальному виду
4.3. Задачи для самостоятельного решения Решить уравнения.
Линейные уравнения ПЕРВОГО порядка Сведения из теории Дифференциальное уравнение первого порядка, разрешенное относительно производной, называется линейным, если его правая часть – линейная функция от
При
Оно является уравнением с разделяющимися переменными, и его общее решение
где
1) Метод вариации произвольной постоянной (метод Лагранжа). Сначала находится общее решение соответствующего линейного однородного уравнения. Решение неоднородного уравнения ищем в виде
получающемся из заменой постоянной
Подставляя в, получаем общее решение уравнения.
Метод Бернулли. Ищем решение уравнения в виде
Подберем
Интегрируя, находим его общее решение
Примеры решения задач 5.2.1. Решить уравнение
◄ Уравнение записано в нормальной форме. Его правая часть является линейной функцией аргумента у. Следовательно, уравнение – линейное. Решаем его методом вариации произвольной постоянной. Сначала находим общее решение однородного уравнения Решение неоднородного уравнения ищем в виде
Итак, общее решение
5.2.2. Решить задачу Коши ◄
Приравняем скобку к нулю и решаем полученное уравнение.
Поскольку нам нужно только частное решение уравнения, то примем
Перемножая u и v, находим общее решение 5.3. Задачи для самостоятельного решения Решить уравнения.
5.3.9. Известно, что сила тока а) УравнениЯ Бернулли Сведения из теории Уравнение Бернулли – это уравнение первого порядка, имеющее в нормальной форме вид
Методы решения те же, что и для линейного неоднородного уравнения, являющегося частным случаем уравнения Бернулли при
Примеры решения задач 6.2.1. Решить уравнение Бернулли ◄ Решаем методом Бернулли
6.3. Задачи для самостоятельного решения
Решить уравнения.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 4028; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.45.159 (0.01 с.) |

 замену переменных: введем новую неизвестную функцию
замену переменных: введем новую неизвестную функцию  , связанную с искомой функцией
, связанную с искомой функцией  соотношением
соотношением  , где
, где  – дифференцируемая функция. Подставляя выражения
– дифференцируемая функция. Подставляя выражения  и
и  через
через  в (3.1), получим для нахождения
в (3.1), получим для нахождения  , которое при удачном выборе замены может оказаться «проще» первоначального. Например, уравнение
, которое при удачном выборе замены может оказаться «проще» первоначального. Например, уравнение
 сводится к уравнению с разделяющимися переменными
сводится к уравнению с разделяющимися переменными .
. .
. . Выразим
. Выразим  . Подставим эти выражения в исходное уравнение и решим полученное уравнение с разделяющимися переменными.
. Подставим эти выражения в исходное уравнение и решим полученное уравнение с разделяющимися переменными. .
. .
. – общее решение уравнения.►
– общее решение уравнения.► , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 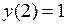 .
. , то естественно сделать замену
, то естественно сделать замену  . Для функции
. Для функции  получим дифференциальное уравнение
получим дифференциальное уравнение  с разделяющимися переменными и начальное условие
с разделяющимися переменными и начальное условие 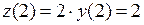 . Разделяем переменные:
. Разделяем переменные:  ,
,  , интегрируем:
, интегрируем: 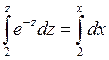 , выражаем z, а затем и y через x
, выражаем z, а затем и y через x ,
,  ,
,  ,
, ,
,  ,
, – искомое решение.►
– искомое решение.► .
3.3.2.
.
3.3.2.  .
Указание: Сделать замену
.
Указание: Сделать замену  .
3.3.5.
.
3.3.5.  .
Указание:
.
Указание:  .
.
 .
3.3.4.
.
3.3.4.  .
Указание: Поскольку
.
Указание: Поскольку 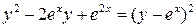 , то рекомедуется сделать замену
, то рекомедуется сделать замену  .
3.3.6.
.
3.3.6.  .
Указание:
.
Указание:  .
.


 .
. и
и  .
. .
. .
. , получим
, получим 
 . Тогда
. Тогда  ,
,  . Для функции
. Для функции  получаем уравнение с разделяющимися переменными:
получаем уравнение с разделяющимися переменными: 


 - общий интеграл. ►
- общий интеграл. ► , удовлетворяющее условию
, удовлетворяющее условию  .
. . Так как х и у входят в правую часть только в виде отношения
. Так как х и у входят в правую часть только в виде отношения  , то это – однородное уравнение. Делаем замену
, то это – однородное уравнение. Делаем замену  . Для функции
. Для функции 

 и начальное условие
и начальное условие  . Разделяем переменные:
. Разделяем переменные:  ,
,  ;
;  ;
;  , и потому
, и потому  – искомое решение.►
– искомое решение.► .
.
 .
.
 .
.
 .
.
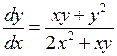 .
4.3.7.
.
4.3.7.  .
.
 .
4.3.8.
.
4.3.8.  .
.
 .
. получаем линейное однородное уравнение
получаем линейное однородное уравнение .
. ,
, – одна из первообразных функции
– одна из первообразных функции  . Общее решение линейного неоднородного уравнения
. Общее решение линейного неоднородного уравнения  можно найти одним из следующих методов.
можно найти одним из следующих методов. ,
, на функцию
на функцию  . Подставляя в уравнение, получаем для новой неизвестной функции
. Подставляя в уравнение, получаем для новой неизвестной функции  . Интегрируя, находим
. Интегрируя, находим
 . Тогда
. Тогда  . Подставляя в уравнение, получим
. Подставляя в уравнение, получим  . Перепишем это уравнение в виде
. Перепишем это уравнение в виде .
. так, чтобы скобка в уравнении обратилась в нуль. Для этого нужно найти какое-нибудь частное решение
так, чтобы скобка в уравнении обратилась в нуль. Для этого нужно найти какое-нибудь частное решение  уравнения с разделяющимися переменными
уравнения с разделяющимися переменными  . Подставляя
. Подставляя 
 .
. . Перемножая найденные значения
. Перемножая найденные значения  и
и  , получим общее решение неоднородного уравнения
, получим общее решение неоднородного уравнения 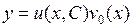 .
. .
. .
.  .
.  .
. , где
, где 

 .
. , где справа буквой С обозначена, как и везде, произвольная постоянная. После преобразований запишем его в виде
, где справа буквой С обозначена, как и везде, произвольная постоянная. После преобразований запишем его в виде . ►
. ► .
. – линейное уравнение. Решаем методом Бернулли:
– линейное уравнение. Решаем методом Бернулли:  . Подставляя
. Подставляя  . Сгруппируем члены, содержащие
. Сгруппируем члены, содержащие  .
.
 .
. , тогда
, тогда  . Подставляя
. Подставляя  .
. . Подставляя в общее решение начальные значения
. Подставляя в общее решение начальные значения  и
и  , получим
, получим  . Искомое решение
. Искомое решение  .►
.► .
.
 .
.
 .
.
 .
.
 .
.
 .
.

 в цепи, имеющей сопротивление
в цепи, имеющей сопротивление  , самоиндукцию
, самоиндукцию  удовлетворяет уравнению
удовлетворяет уравнению  , где
, где  – электродвижущая сила. Найти силу тока
– электродвижущая сила. Найти силу тока  , в случаях
, в случаях , б)
, б)  .
. ,
,  .
. .
. .
. . Подберем v, так чтобы
. Подберем v, так чтобы  . Тогда
. Тогда  . Возьмем
. Возьмем 
 – общее решение.►
– общее решение.► .
.
 .
.

 .
.



