
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
УравнениЯ в полных дифференциалахСодержание книги Поиск на нашем сайте
Сведения из теории Будем рассматривать дифференциальное уравнение первого порядка, заданное в дифференциальной форме
В нормальной форме оно имеет вид
Уравнение называется уравнением в полных дифференциалах, если его левая часть является дифференциалом некоторой функции
Если функции
– необходимое и достаточное условие того, что является в области D уравнением в полных дифференциалах. Так как уравнение можно переписать в виде
где Примеры решения задач 7.2.1. Решить уравнение ◄ Данное уравнение не принадлежит ни к одному из типов, которые мы умеем определять по их нормальной форме. Перепишем исходное уравнение в дифференциальной форме
Область определения этого уравнения
Таким образом, мы имеем уравнение в полных дифференциалах. Находим по формуле при Итак, общий интеграл уравнения имеет вид 7.3. Задачи для самостоятельного решения
Смешанные задачи на дифференциальные уравнения первого порядка Примеры решения задач 8.1.1. Для каждого из дифференциальных уравнений
определить, является ли оно уравнением одного из следующих типов: 1) уравнением с разделяющимися переменными, 2) однородным уравнением, 3) линейным уравнением, 4) уравнением Бернулли (но не линейным уравнением), 5) уравнением в полных дифференциалах, 6) не является уравнением типов 1) – 5). ◄ Уравнение приведем нормальному виду Уравнение имеет нормальный вид. Правую часть можно представить в виде произведения функции от x на функцию от y:
Уравнение записано в дифференциальной форме. Однако уравнением в полных дифференциалах оно не является, так как
Уравнение равносильно уравнению Уравнение является уравнением в полных дифференциалах, так как совпадают производные
а область определения Ясно, что уравнение не принадлежит ни одному из типов 1) – 4) (хотя строго доказать это совсем непросто). Записав уравнение в дифференциальной форме
8.2. Задачи для самостоятельного решения Решить следующие дифференциальные уравнения.
Для каждого из следующих дифференциальных уравнений определить, является ли оно уравнением одного из типов: 1) уравнением с разделяющимися переменными, 2) однородным уравнением, 3) линейным уравнением, 4) уравнением Бернулли (но не линейным уравнением), 5) уравнением в полных дифференциалах, 6) не является уравнением типов 1) – 5).
Дифференциальные уравнения Высших порядков Сведения из теории Дифференциальным уравнением n-го порядка называется функциональное уравнение вида Будем рассматривать только уравнения, которые можно разрешить относительно старшей производной:
Задача Коши для уравнения состоит в том, что ищется решение уравнения
где Теорема существования и единственности. Если функция Общим решением уравнения n-го порядка в области Краевая задача для уравнения n -го порядка
Примеры решения задач 9.2.1. Дано уравнение второго порядка
Убедиться, что ◄ Находим производные функции
Это система линейных уравнений относительно
Таким образом, а) При б) Подберем
Таким образом,
9.3. Задачи для самостоятельного решения
9.3.1. Убедиться, что Дифференциальные уравнения,
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 543; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.32.6 (0.009 с.) |

 .
. .
.
 .
. и
и  непрерывны вместе со своими производными в некоторой односвязной области[1] D, то равенство
непрерывны вместе со своими производными в некоторой односвязной области[1] D, то равенство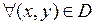
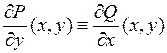
 , то
, то  - его общий интеграл. Функцию u можно найти по формуле
- его общий интеграл. Функцию u можно найти по формуле ,
, – какая-нибудь точка из D.
– какая-нибудь точка из D. .
. .
. – односвязна. Проверяем условие.
– односвязна. Проверяем условие.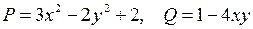 .
. 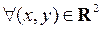
 .
.
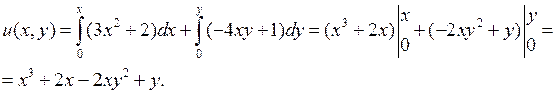
 . ►
. ► .
.
 .
.
 .
.
 .
.
 .
.
 .
.
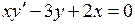 ,
,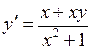 ,
, ,
, ,
, ,
,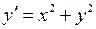
 . В его правую часть переменные входят только в виде отношения
. В его правую часть переменные входят только в виде отношения  , следовательно, – однородное уравнение и его можно решать заменой
, следовательно, – однородное уравнение и его можно решать заменой  ,
,  . С другой стороны, правая часть
. С другой стороны, правая часть 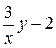 является линейной функцией переменной y и уравнение является линейным. Поэтому его можно решать, например, методом Бернулли.
является линейной функцией переменной y и уравнение является линейным. Поэтому его можно решать, например, методом Бернулли. , поэтому это уравнение с разделяющими переменными. Поскольку правую часть можно представить в виде
, поэтому это уравнение с разделяющими переменными. Поскольку правую часть можно представить в виде  , то уравнение является и линейным (линейным неоднородным). Однако нет смысла решать его ни методом Бернулли, ни методом Лагранжа (то есть делать замену переменных, сводящую уравнение к уравнению с разделяющимися переменными) ибо переменные изначально разделяются.
, то уравнение является и линейным (линейным неоднородным). Однако нет смысла решать его ни методом Бернулли, ни методом Лагранжа (то есть делать замену переменных, сводящую уравнение к уравнению с разделяющимися переменными) ибо переменные изначально разделяются. ,
,  и
и 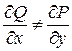 . Приведем уравнение (8.3) к нормальному виду
. Приведем уравнение (8.3) к нормальному виду  . Правая часть является отношением однородных многочленов первой степени. Разделив числитель и знаменатель на x, запишем уравнение в виде
. Правая часть является отношением однородных многочленов первой степени. Разделив числитель и знаменатель на x, запишем уравнение в виде  , то есть уравнение имеет вид и, следовательно, является однородным.
, то есть уравнение имеет вид и, следовательно, является однородным. , имеющему вид, то есть оно является уравнением Бернулли.
, имеющему вид, то есть оно является уравнением Бернулли.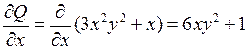 и
и  ,
, , нетрудно убедиться, что условие не выполняется, и потому это уравнение не является уравнением в полных дифференциалах. Итак, для уравнения имеет место случай 6), то есть мы не можем решить уравнение разобранными выше методами. ►
, нетрудно убедиться, что условие не выполняется, и потому это уравнение не является уравнением в полных дифференциалах. Итак, для уравнения имеет место случай 6), то есть мы не можем решить уравнение разобранными выше методами. ► .
.
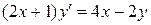 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
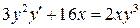 .
.
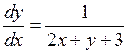 .
.
 .
.
 .
.
 .
.
 .
.
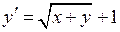 .
.
 .
.
 .
.
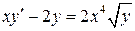 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
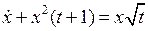 .
.
 .
.
 .
.
 .
.
 .
.
 , связывающее независимую переменную
, связывающее независимую переменную  , искомую функцию
, искомую функцию  – решение уравнения и ее производные
– решение уравнения и ее производные  .
. .
. , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям ,
, – заданный набор из
– заданный набор из  -го числа.
-го числа. в окрестности точки
в окрестности точки  в
в  непрерывна и имеет непрерывные частные производные, то на некотором промежутке
непрерывна и имеет непрерывные частные производные, то на некотором промежутке 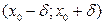 существует (и притом единственное) решение
существует (и притом единственное) решение  называется семейство
называется семейство  его решений, зависящее от n параметров
его решений, зависящее от n параметров  и содержащее решение любой задачи Коши, если
и содержащее решение любой задачи Коши, если  состоит в том, что ищется решение уравнения
состоит в том, что ищется решение уравнения  или ее производных более чем в одной точке. Число условий обычно совпадает с порядком уравнения.
или ее производных более чем в одной точке. Число условий обычно совпадает с порядком уравнения. .
. – общее решение уравнения. Найти а) решение, удовлетворяющее начальным условиям
– общее решение уравнения. Найти а) решение, удовлетворяющее начальным условиям  ,
,  ; б) решение, удовлетворяющее граничным условиям
; б) решение, удовлетворяющее граничным условиям 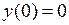 ,
,  .
. ,
,  . Подставляя
. Подставляя  и
и  в уравнение, убеждаемся, что оно обращается в тождество
в уравнение, убеждаемся, что оно обращается в тождество  и
и  . Пусть
. Пусть  – произвольные числа. Покажем, что можно подобрать
– произвольные числа. Покажем, что можно подобрать 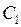 и
и  так, чтобы
так, чтобы 
 ,
,  .
.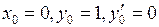 , получаем
, получаем  ,
,  – решение, удовлетворяющее начальным условиям
– решение, удовлетворяющее начальным условиям 
 ,
,  .
. – решение краевой задачи
– решение краевой задачи  является общим решением уравнения
является общим решением уравнения  . Найти а) решение, удовлетворяющее начальным условиям
. Найти а) решение, удовлетворяющее начальным условиям 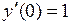 ; б) решение, удовлетворяющее граничным условиям
; б) решение, удовлетворяющее граничным условиям  .
.


