Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
метод вариации произвольных постоянныхСодержание книги Поиск на нашем сайте
Сведения из теории Метод вариации произвольных постоянных (метод Лагранжа) решения линейного неоднородного уравнения
состоит в следующем. Пусть известна фундаментальная система решений
соответствующего линейного однородного уравнения
Общее решение неоднородного уравнения ищется в виде
получающемся из общего решения однородного уравнения заменой произвольных постоянных
Определитель этой системы – определитель Вронского
Интегрируя, находим:
где
Подставляя найденные
Примеры решения задач 14.2.1. Решить уравнение ◄Соответствующее однородное уравнение
Производные
Для нашего уравнения это будет система
Решаем ее по формулам Крамера.
14.2.2. Решить уравнение ◄ Соответствующее однородное уравнение имеет постоянные коэффициенты. Его характеристическое уравнение
Система для этого уравнения имеет вид
Ее можно решать по формулам Крамера, но удобнее воспользоваться спецификой системы. Складывая первое и третье уравнение, получаем
Умножая второе уравнение на
Из второго уравнения
Подставляя
14.3. Задачи для самостоятельного решения Решить уравнения.
Список литературы
1. Бугров, Я.С. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного / Я.С. Бугров, С.М. Никольский. – М.: Наука, 1985. – 464с.
2. Пискунов, П.С. Дифференциальное и интегральное исчисление для втузов». Т. 2, 13 изд., М.: Наука, 1985. -560 с. 3. Сборник задач по высшей математике для вузов. Ч.2. Специальные разделы математического анализа. / Под ред. А.В. Ефимова, Б.П. Демидовича. – М.: Наука, 1986. – 366 с. 4. Данко, П.Е. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – 5-е изд., исп. – М.: Высшая школа, 1999. – 304 с. 5. Филиппов, А.Ф. Сборник задач по дифференциальным уравнениям М., Наука, 1985. – 128 с. 6. Краснов, М.Л. Сборник задач по дифференциальным уравнениям / М.Л. Краснов, А.И. Киселев, Г.И. Макаренко. - М.: Высшая школа, 1978, - 388с. 7. Карташов, А.П. Обыкновенные дифференциальные уравнения и основы вариационного исчисления / А.П. Карташов, Б.Л. Рождественский. – М.: Наука, 1980. – 287 с. 8. Самойленко, А.М. Дифференциальные уравнения: Примеры и задачи / А.М. Самойленко, С.А. Кривошея, Н.А. Перестюк. – 2-е изд., перераб. – М.: Высшая школа, - 1989. – 383 с. 9. http://www. krelib.com [Электронный ресурс].
Ответы 2.3.2. 2.3.8. 2.3.14. 3.3.2. 4.3.2. 4.3.8. 5.3.6. 5.3.9. а) 6.3.3. 7.3.2. 8.2.2. 8.2.8. 8.2.12. НЛДУ1. 8.2.14. ОЛДУ1. 8.2.16. с разделяющимися переменными. 8.2.18. однородное. 8.2.20. уравнение Бернулли. 9.3.1. а) 10.3.2. 10.3.6. 10.3.12. 11.3.1. 12.3.14. 13.3.2. 13.3.6. 13.3.10. 13.3.14. 13.3.16. 13.3.18. 13.3.20. 14.3.2. 14.3.4. 14.3.6. Задания для РГР Задания 1-15 – решить данные дифференциальные уравнения.
Задание 16 – по данным корням характеристического уравнения некоторого линейного однородного дифференциальные уравнения, найти это дифференциальное уравнение и записать его общее решение. Для соответствующего неоднородного уравнения с данной функцией
Задание 17. А) решить данную систему дифференциальных уравнений. Б) Исследовать положение равновесия В) Определить тип положения равновесия и изобразить фазовый портрет.
Задание 18. А) Убедиться, что Б) Исследовать на устойчивость положение равновесия по первому приближению.
В) Определить тип положения равновесия в окрестности точки
Вариант 1
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16.
17. 18. Вариант 2 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Вариант 3
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Вариант 4
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Вариант 5 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Вариант 6
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Вариант 7
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Вариант 8
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Вариант 9
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Вариант 10
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Вариант 11 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Вариант 12
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Вариант 13
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Вариант 14
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Вариант 15
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Вариант 17
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Вариант 18
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Вариант 19
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Вариант 20
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Вариант 21
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Вариант 22
1. 2. 3. 4. 5. 6. 7. 8. | ||||||||||
|
| Поделиться: |
.
,
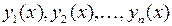
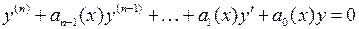на функции 
. Производные 
этих функций находятся из системы линейных алгебраических уравнений
– линейно независимой системы функций 
.
,, …, 
,
.
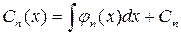имеет переменные коэффициенты и не может быть решено методом, описанным в п.12. Его ф.с.р. указана в задаче 11.3.1: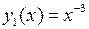 
, 
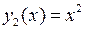. Общее решение неоднородного уравнения ищем в виде
.
и 
находятся из системы линейных алгебраических уравнений, имеющей при 
вид
,
,
,
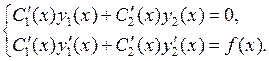
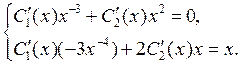
или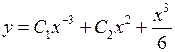 
– общее решение.►
.
имеет корни 
, 
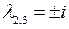. Им в ф.с.р. соответствуют решения 
. Общее решение уравнения ищем в виде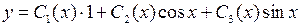
.
,
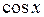, третье – на (
) и складывая их получим 
.
.
.
, 
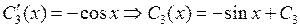и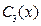 
в, получаем общее решение
.►
.
.
.
.
.
.
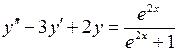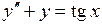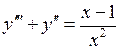. 2.3.4. 
. 2.3.6. 
.
. 2.3.10. 
. 2.3.12. 
.
. 2.3.16. 
. 2.3.17. 60 мин. 2.3.19. 
18,4 мин.
. 3.3.4. 
. 3.3.6. 
.
. 4.3.4. 
. 4.3.6. 
.
. 5.3.2. 
. 5.3.4. 
.
. 5.3.8. 
.
; б) 
.
. 6.3.4. 
.
. 7.3.4.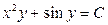 
. 7.3.6. 
.
. 8.2.4.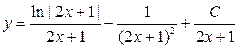 
. 8.2.6. 
.
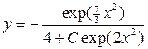. 8.2.10. 
.
; б)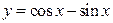 
.
. 10.3.4. 
.
. 10.3.8. 
. 10.3.10. 
.
. 10.3.14. 
.
. 11.3.2. 
. 12.3.2. 
. 12.3.4. 
. 12.3.6. 
. 12.3.8. 
. 12.3.10. 
. 12.3.12. 
.
.
. 13.3.4. 
.
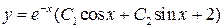. 13.3.8. 
.
. 13.3.12. 
.
.
.
.
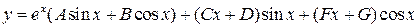. 13.3.22. 
.
.
.
.
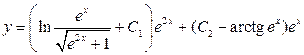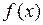в правой части записать общий вид частного решения неоднородного уравнения.
на устойчивость.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
, 
, 
, 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
, 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
, 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
, 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
, 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. 
.
,
.
.
.
.
, 
.
.
.
.
.
.
.
.
.
.
, 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
, 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
, 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
, 
.
.
.
.
.
.
.
.
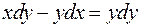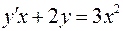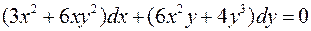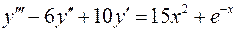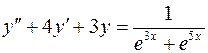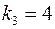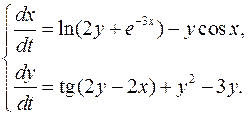
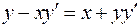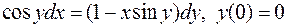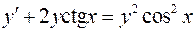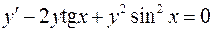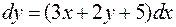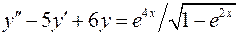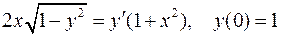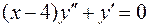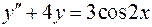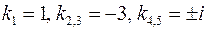
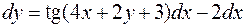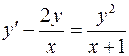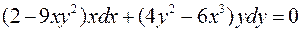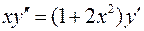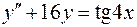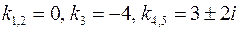
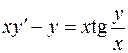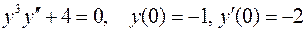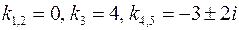
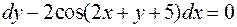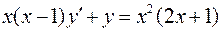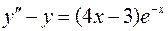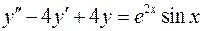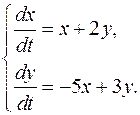
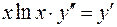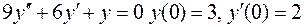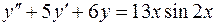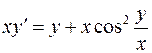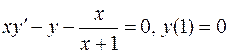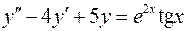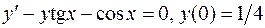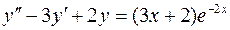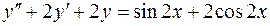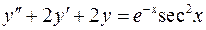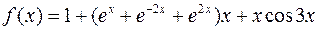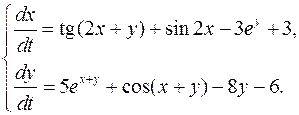
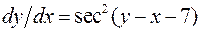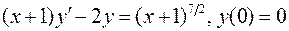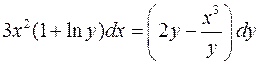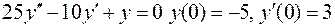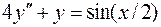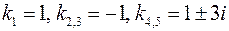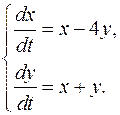
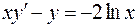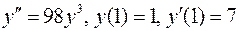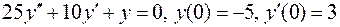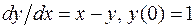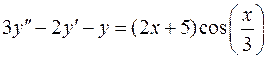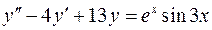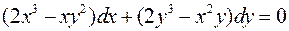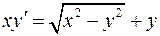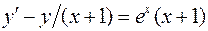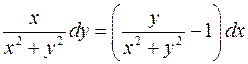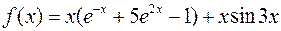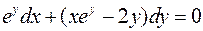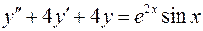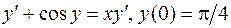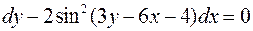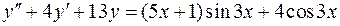