
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Функции многих независимых переменныхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Для решения задач по этой теме обратите внимание на то, что правила вычисления частных производных совпадают с правилами, указанными для функций одного аргумента, и если отыскивается, например, частная производная по переменной х, то переменная у считается при этом константой. Обратите внимание на вычисление производной по заданному направлению и на связь этой производной с градиентом функции. При исследовании функции z = f(x, y) на экстремум (при условии, что она дважды дифференцируема) пользуйтесь следующими правилами: 1) найдите честные производные функции z = f(x, y) и решите систему уравнений Точки, в которых частные производные равны нулю, называются стационарными точками. Пусть одна из них Р0 (х0, у0). 2) Найдите частные производные второго порядка функции z = f(x, y) и вычислите их значения в точке Р0 (х0, у0). Положим А = 3) Вычислите определитель
Если окажется, что
Вопросы для самопроверки 1. Как определяется функция нескольких переменных? 2. Дайте определение непрерывности функции нескольких переменных. 3. Что называется частной производной функции нескольких переменных? 4. Какова геометрическая интерпретация частной производной функции двух аргументов? 5. Что называется полным дифференциалом функции двух аргументов? 6. Как вычисляется производная сложной функции? 7. Как вычисляется производная по направлению и какова её связь с градиентом функции? 8. Сформулируйте правило исследования функции двух переменных на экстремум.
Тема 2. Кратные и криволинейные интегралы Для решения задач по этой теме необходимо, прежде всего, разобраться в правилах перехода от двойного интеграла по правильной области D к двукратному (повторному) интегралу: если D – правильная область, ограниченная в направлении к оси Оу линиями у=
Обратите внимание на переход в двойном интеграле к полярным координатам. Изучите механические приложения двойного интеграла. При изучении криволинейного интеграла разберитесь в способе его сведения к определенному интегралу по некоторому отрезку. Изучите условия независимости криволинейного интеграла от пути интегрирования.
Вопросы для самопроверки 1. Какая область называется правильной? 2. Как свести двойной интеграл по правильной области к двукратному? 3. Каковы правила перехода в двойном интеграле к полярным координатам? 4. Как вычисляется объем тела с помощью двойного интеграла? 5. Как вычисляется масса и центр тяжести плоской пластины при заданной поверхностной плотности? 6. Какие задачи приводят к понятию криволинейного интеграла? 7. Как вычисляется криволинейный интеграл? 8. Как влияет на значение криволинейного интеграла направление обхода контура интегрирования? 9. Каковы условия независимости криволинейного интеграла от пути интегрирования? 10. Какова связь независимости криволинейного интеграла от пути интегрирования и равенства нулю криволинейного интеграла по любому замкнутому контуру?
КОНТРОЛЬНАЯ РАБОТА № 4 В задачах 301‑310 вычислить частные производные первого и второго порядков от заданных функций. 301. z= 8 ln (xy2) + 10xy2 + 8x. 302. z= 2 tg (xy) – 7x2y + 6x. 303. z= 8 cos (xy) – 3x – 12x4y. 304. z= 3 ctg (x2y) + 7y – 6xy2. 305. z= x sin (xy) + 8x2y2 – 7x. 306. z= 6e 307. z= 308. z= 9e 309. z= 8 ln (x2 + y2) – 6x2y3 + 8x – 1. 310. z= 3 Решение типового примера. Пусть При вычислении частной производной
Аналогично поступаем при вычислении
Используя те же правила, вычисляем частные производные второго порядка:
В задачах 311 – 320 задана функция z = f(x, y). Найти градиент и производную этой функции в заданной точке М(х0, у0) в направлении вектора 311. z= tg x + x – 2 sin y, M( 312 z= 313. z= 2 cos (x +y) +2x, M( 314. z= 3 tg x – 2x cos y, M( 315. z= ln (x2 + y2), M(3, 4), 316. z= x sin(x+y) – 1, M( 317. z= x tg y + cos x, M( 318. z= 2x2 + 3xy + y2, M(2; 1), 319. z= 320. z= 5x2 + 6xy, M(2; 1), Решение типового примера. Пусть z = 2 tg x – 3x cos y. Найдем градиент и производную этой функции в точке М
Вычислим теперь значения этих производных в точке М
Таким образом, (grad z)M = Производная в направлении вектора
т.е. в нашем случае
В задачах 321 – 340 найти экстремум заданной функции. 321. z= 2x2 – xy + y2 – 3x – y + 1. 322. z= x2 + 2xy – y2 + 4x. 323. z= 2x2 + xy – y2 – 7x + 5x + 2. 324. z= x2 + y2 = 9xy + 27. 325. z= 3x2 + xy – 6y2 – 6x – y + 9. 326. z= 5x2 – 3xy + y2 + 4. 327. z= 4x2 – 2xy + y2 – 2x – 4y + 1. 328. z= x2 + 3y2 + x - y. 329. z= 8x2 – xy + 2y2 – 16x + y – 1. 330. z= 3 – 2x2 – xy – y2. 331. z= 6xy – 2x2 – y2 – 14x + 5. 332. z= 3xy – x2 – 3y2 – 6x + 9y - 4. 333. z= 10xy – 3x2 – 2y2 – 26x + 18y – 1. 334. z= x2 + y2 – xy + x + y +2. 335. z= 3 – 3x2 + 5y2 – 8xy + 4x + 26y. 336. z= 3x2 + 3y2 + 5xy + x – y + 5. 337. z= 5x2 – 3x2 + 2xy – 18x – 10y + 4. 338. z= x2 + 2xy – y2 + 6x – 10y + 1. 339. z= 2x2 – 3y2 + 2xy – 10x + 16y – 7. 340. z= 4 – 5x2 – y2 – 4xy + 4x – 2y.
Решение типового примера. Пусть z = 2x2 – xy + 3y2 – 2x – 11y + 1. Находим частные производные функции:
Воспользовавшись необходимыми условиями экстремума, находим стационарные точки. Для этого решаем систему уравнений
откуда х = 1; у = 2. Таким образом, стационарной является точка М (1, 2). Находим значения частных производных второго порядка в точке М:
Составляем выражение Так как
В задачах 341 – 360 с помощью двойного интеграла вычислить координаты центра тяжести фигуры, ограниченной заданными линиями (поверхностную плотность считать равной единице). 341. x2 + 4y2 = 1; -x + 2y = 1. 342. x2 + y2 = 16; x + y = 4. 343. x2 + y2 = 9; x + y – 3 = 0. 344. 345. x2 + 25y2 = 1; x – 5y = 1. 346. 16x2 + 25y2 = 1; 4x – 5y = 1. 347. 4x2 + 25y2 = 1; 2x – 5y – 1 = 0. 348. 4x2 + 9y2 = 1; 2x – 3y – 1 = 0. 349. x2 + y2 = 4; x + y + 2 = 0. 350. 9x2 + 25y2 = 1; 3x + 5y – 1 = 0. 351. y2 = 2x + 4; y2 = - 352. y2 = 3x – 2; y2 = - 353. y2 = 9x + 9; y2 = -x + 9. 354. y2 = 4x + 4; y2 = -x + 4. 355. x2 = 2y + 4; x2 = -y + 4. 356. x2 = y + 2; x2 = -y + 2. 357. x2 = 3y + 9; x2 = -y + 9. 358. x2 = 3y + 7; x2 = -y + 7. 359. x2 = 25y + 25; x2 = 5y + 25. 360. x2 = 16y + 4; x2 = 4y + 4.
Решение типовых примеров. Пример 1. Найти координаты центра тяжести фигуры, ограниченной эллипсом Решение. В случае однородной пластины, занимающей область D плоскости хОу, координаты центра тяжести
где S – площадь области D,
В рассматриваемом случае (см. рис. 7) фигура ограничена кривыми S = =
Рис. 7 Для вычисления полученного интеграла используем замену
Итак,
Первый из полученных интегралов вычисляется с помощью замены Отсюда
Наконец,
Пример 2. Найти координаты центра тяжести фигуры, ограниченной линиями Решение.
Рис.8
Поскольку фигура симметрична относительно оси Ох, то
Таким образом,
В задачах 361–380 вычислить объем тела, ограниченного заданными поверхностями и расположенного в первом октанте. 361. x2 + y2 + z2 = 16; x2 + y2 = 4. 362. z = 2x + y; y = 363. x2 + y2 = 2; x + y + z = 2; z = 0. 364. z = 3x; y = 365. x2 + y2 = 366. z = x2 + y2 + 1; x + y = 3; x = 0; y = 0; z = 0. 367. x2 + y2 + z2 = 36; z = 0; y = x; y = 0. 368. z = 6 – x – y; 2x + y = 4; x = 0; y = 0; z = 0. 369. x2 + y2 = 370. y = 371. x2 + y2 = 5; z = x2 + y2. 372. 4x + 3y – 12 = 0; z = x2 + 1; x = 0; y = 0; z = 0. 373. x2 + y2 = 18; x + y + z = 6; z = 0. 374. z = x + y + 2; y = 2x: x = 3; x = 0; y = 0; z = 0. 375. z = 8 - x2 - y2; x2 + y2 = 3; y = 376. x + y = 1; z = 9x2 + 3y2 + 2; x = 0; y = 0; z = 0. 377. z = 1 - x2 - y2; y = 378. x + 2y = 2; z = 8 – 2x2 + 4y; x = 0; y = 0; z = 0. 379. x2 + y2 = 18; y = x; y = 0; x + y + z = 6; z =0. 380. x2 + y2 + z2 = 4; x2 + y2 = 3.
Решение типовых примеров. Пример 1. Вычислить объем тела, ограниченного поверхностями х2 + у2 = 8, х =0; у = 0; z = 0; х + у + z = 4 и расположенного в первом октанте. Решение. Заданное тело ограничено круговым цилиндром х2 + у2 = 8, координатными плоскостями и плоскостью х + у + z = 4. Объем цилиндрического тела, ограниченного сверху поверхностью z = f(x,y), снизу плоскостью z = 0 и по бокам прямой цилиндрической поверхностью, вырезающей на плоскости хОу область D, вычисляется по формуле V = В данном случае область D – это область круга радиуса
Пример 2. Найти объем тела, ограниченного поверхностями х2+у2 = 9; х2+z2 = 9 и расположенного в первом квадранте. Решение. Заданное тело ограничено двумя круговыми цилиндрами. Искомый объем выражается интегралом
где D – четверть круга радиуса, равного 3. Таким образом,
В задачах 381–390 вычислить работу, совершаемую переменной силой 381. L – дуга параболы y = 2x2 + 1; M (0;1), N (2;9) 382. L – дуга параболы y = 2x3 + 1; M (1;3), N (2;10) 383. L – дуга параболы y = 7x2 +2х; M (0;0), N (2;32) 384. L – дуга параболы y = 3x2 + х; M (1;3), N (2;25) 385. L – дуга параболы y = 3x2 + х; M (1;4), N (3;30) 386. L – отрезок прямой, соединяющий точки M (1;2), N (4;6) 387. L – дуга кубической параболы y = x3+1; M (1;3), N (2;10) 388. L – дуга параболы y = x3 ; M (0;1), N (3;3) 389. L – дуга параболы y = 3x2 + 2; M (2;14), N (3;29) 390. L – дуга параболы y = 2x2 ; M (1;2), N (3;10)
Решение типового примера. Вычислим работу, совершаемую переменой силой
Преобразуем этот криволинейный интеграл к определенному интегралу, для чего вычислим дифференциал
В задачах 391–400 установить независимость от пути интегрирования и вычислить криволинейный интеграл по контуру, связывающему точки М(1;2) и N(3;5). 391. 392. 393. 394. 395. 396. 397. 398. 399. 400.
Решение типового примера. Вычислим криволинейный интеграл
по контуру, соединяющему точки М(1;1) и N(2;30), предварительно убедившись в независимости его от пути интегрирования. В данном случае выполнено условие независимости криволинейного интеграла от пути интегрирования
где Р = х2 + 3ху, Q = Выберем в качестве контура интегрирования наиболее простой контур, связывающий точки М и N, например, ломанную, звенья которой параллельны осям координат:
Рис. 9 Имеем на первом участке у =1, dy =0, 1 Таким образом,
Указания к выполнению контрольной работы № 5
Тема 1. Дифференциальные уравнения
Для того чтобы успешно решить задачи этой темы, следует особое внимание обратить на следующие типы дифференциальных уравнений: 1) однородные уравнения первого порядка, 2) линейные уравнения первого порядка, 3) уравнение Бернулли, 4) линейные однородные уравнения второго порядка с постоянными коэффициентами, 5) линейные неоднородные уравнения второго порядка с постоянными коэффициентами и с правой частью уравнения, представленной произведением показательной функции и многочлена. Однородным уравнением первого порядка называется дифференциальное уравнение вида
если функция
Однородные дифференциальные уравнения первого порядка легко приводятся к виду
где правая часть зависит лишь от отношения аргументов. С помощью подстановки Линейным уравнением первого порядка называется уравнение вида
где
или
Если подобрать
каждое из которых есть дифференциальное уравнение с разделяющимися переменными. Этим же приемом можно найти решение и уравнения Бернулли
где Линейным однородным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
где p, q – действительные числа. Чтобы найти общее решение этого уравнения, достаточно найти два линейно независимых частных решения, для отыскания которых следует прежде решить квадратное уравнение (которое называют характеристическим уравнением)
Если корни характеристического уравнения k 1, k 2 действительны и различны, то общее решение Y исходного дифференциального уравнения имеет вид
Если корни характеристического уравнения действительны и равны, т. е. k 1 = k 2, то общее решение исходного дифференциального уравнения имеет вид
Наконец, если характеристическое уравнение не имеет вещественных корней (т.е. его дискриминант p 2 – 4 q отрицателен), то общее решение исходного дифференциального уравнения имеет вид
где Общее решение линейного неоднородного дифференциального уравнения
где
где Y – общее решение соответствующего линейного однородного уравнения, 1) если число y не является корнем характеристического уравнения, то
где 2) если γ совпадает с одним из корней характеристического уравнения, то
3) если оба корня характеристического уравнения равны γ, то
Вопросы для самопроверки
1. Сформулируйте теорему существования и единственности решения дифференциального уравнения первого порядка. 2. Что называется общим решением дифференциального уравнения? 3. Что называется частным решением дифференциального уравнения? 4. Какой вид имеет дифференциальное уравнение с разделяющимися переменными? Как найти общее решение (общий интеграл) этого уравнения? 5. Какое уравнение называется однородным дифференциальным уравнением первого порядка? Как найти его общий интеграл? 6. Приведите пример линейного дифференциального уравнения первого порядка. Как найти его общее решение? 7. Каковы свойства решений линейных однородных уравнений второго порядка? 8. Какой вид имеет общее решение линейного однородного уравнения второго порядка? 9. Укажите вид общего решения линейного неоднородного уравнения второго порядка.
Тема 2. Ряды
Для решения задач этой темы необходимо усвоить несколько признаков сходимости для числовых рядов (необходимый признак сходимости, признаки сравнения рядов, признак Даламбера, признак Лейбница). Далее изучите понятия абсолютной и условной сходимости числовых рядов. Разберите метод отыскания радиуса сходимости степенного ряда, основанный на признаке Даламбера. В приложениях степенных рядов к приближенному вычислению определенного интеграла вам потребуются следующие разложения элементарных функций в степенные ряды: 1. 2. 3. 4. Обратите внимание на то, что приближенное вычисление определенного интеграла нередко приводит к представлению его в виде суммы сходящегося знакочередующегося ряда с невозрастающими по абсолютной величине членами. При вычислении такого интеграла с требуемой точностью нужно просуммировать столько членов соответствующего ряда, чтобы абсолютная величина первого отброшенного члена не превосходила заданной точности. При изучении рядов Фурье обратите внимание на способы разложения в ряд Фурье функции, заданных на отрезке
Вопросы для самопроверки
1. Какой ряд называется сходящимся (расходящимся)? 2. Сформулируйте необходимое условие сходимости ряда. 3. Сформулируйте признаки сравнения знакоположительных рядов. 4. В чем состоит признак Даламбера? 5. Для каких рядов применяется признак Лейбница? В чем его сущность? 6. Как найти радиус сходимости степенного ряда? 7. Сформулируйте теорему о почленном дифференцировании степенного ряда. 8. как вычисляются коэффициенты ряда Маклорена для заданной функции? 9. Напишите разложения в ряд Маклорена функций ex, sin x, cos x, arctg x, arcsin x, (1 + x)n. 10. Как используются степенные ряды в приближенных вычислениях?
КОНТРОЛЬНАЯ РАБОТА № 5
В задачах 401–420 найти общее решение (общий интеграл) дифференциальных уравнений первого порядка.
Решение типового примера. Найти общее решение (общий интеграл) дифференциального уравнения Решение. Правая часть уравнения
Продолжаем преобразования:
Производим разделение переменных:
После интегрирования обеих частей уравнения получаем
Таким образом,
Потенцируя, находим
или
Итак, общий интеграл исходного уравнения приобретает вид
где С – произвольная постоянная.
В задачах 421 – 440 найти частное решение дифференциального уравнения, удовлетворяющее указанному начальному условию.
Решение типового примера. Найти частное решение дифференциального уравнения Решение. Заданное дифференциальное уравнение является уравнением Бернулли. Полагаем
Подберем функцию
Для определения функции
или
Это дифференциальное уравнение с разделяющимися переменными относительно неизвестной функции | ||||
|
| Поделиться: |

 .
. , В =
, В =  , С =
, С = 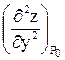 .
.
 = АС – В2.
= АС – В2.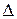 > 0, то функция z = f(x, y) в точке Р0 (х0, у0) имеет максимум при А < 0 и минимум при А > 0; если же
> 0, то функция z = f(x, y) в точке Р0 (х0, у0) имеет максимум при А < 0 и минимум при А > 0; если же  , у=
, у= 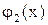 , (
, ( ,
, 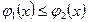 ), то
), то .
. + 3(x2 + y2) + 3.
+ 3(x2 + y2) + 3. +3x4y – 8x – 2.
+3x4y – 8x – 2. - 5xy3 – 3y + 2.
- 5xy3 – 3y + 2. - 4y2x + 3y - 2.
- 4y2x + 3y - 2. .
. переменную
переменную  рассматриваем как постоянную величину. Пользуясь правилом дифференцирования функции одного аргумента и, в частности, правилом дифференцирования сложной функции, получаем
рассматриваем как постоянную величину. Пользуясь правилом дифференцирования функции одного аргумента и, в частности, правилом дифференцирования сложной функции, получаем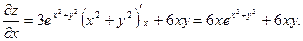
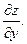 Считая
Считая 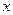 постоянной величиной, получаем
постоянной величиной, получаем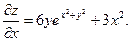



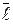 , составляющего угол
, составляющего угол 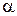 с положительным направлением оси Ох.
с положительным направлением оси Ох. ),
), 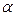 =
=  .
. , M(1; -1),
, M(1; -1),  ),
),  .
. .
.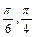 ),
), 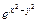 , M(2,2),
, M(2,2),  в направлении, составляющем угол
в направлении, составляющем угол  с положительным направлением оси Ох. Для этого вычислим частные производные функции:
с положительным направлением оси Ох. Для этого вычислим частные производные функции:


 .
. ,
, .
.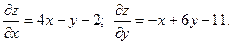

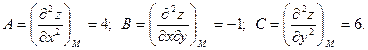
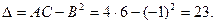
 и
и  , делаем вывод о наличии минимума в точке М (1, 2). При этом минимальное значение функции равно z min = -11.
, делаем вывод о наличии минимума в точке М (1, 2). При этом минимальное значение функции равно z min = -11.
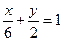 .
. x + 1.
x + 1. x + 1.
x + 1.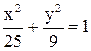 и прямой
и прямой  (поверхностную плотность в каждой точке считать равной единице).
(поверхностную плотность в каждой точке считать равной единице).
 находят по формулам:
находят по формулам:
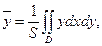
 .
.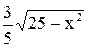 и у = 3(1 -
и у = 3(1 -  ) при
) при  . Поэтому
. Поэтому


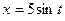 . При этом
. При этом  . Отсюда
. Отсюда

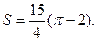 Далее
Далее

 . Тогда
. Тогда 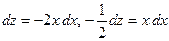 и
и 

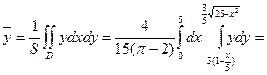


 = 0. Вычислим первую координату центра тяжести
= 0. Вычислим первую координату центра тяжести 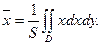



 ,
, 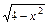 ; x = 0; y = 0; z = 0.
; x = 0; y = 0; z = 0. ; y = 0; z = 0.
; y = 0; z = 0.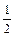 ; x + y + z = 1; z = 0.
; x + y + z = 1; z = 0.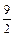 ; x + y + z = 3; z = 0.
; x + y + z = 3; z = 0.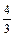
 x; y = 0.
x; y = 0. ; z = 0.
; z = 0.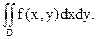
 , расположенная в первом квадранте, поэтому рассматриваемый интеграл удобно вычислять в полярных координатах. При этом
, расположенная в первом квадранте, поэтому рассматриваемый интеграл удобно вычислять в полярных координатах. При этом 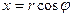 ,
, 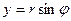 ,
,  . Таким образом,
. Таким образом,


 ,
,
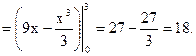
 на криволинейном пути L, соединяющем заданные точки М и N.
на криволинейном пути L, соединяющем заданные точки М и N.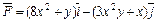









 на дуге параболы у = 3х2 + х, соединяющей точки М (1; 4) и N (3; 29). Для этого необходимо вычислить криволинейный интеграл
на дуге параболы у = 3х2 + х, соединяющей точки М (1; 4) и N (3; 29). Для этого необходимо вычислить криволинейный интеграл .
. и заметим, что переменная
и заметим, что переменная 
 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.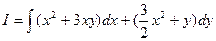
 ,
, . Действительно,
. Действительно,  ,
,  .
.
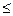 х
х  .
.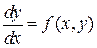 ,
, удовлетворяет условию
удовлетворяет условию .
.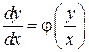 ,
, это уравнение приводится к уравнению с разделяющимися переменными.
это уравнение приводится к уравнению с разделяющимися переменными. ,
,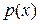 ,
,  – заданные непрерывные функции от аргумента х. Решение линейного уравнения ищут в виде
– заданные непрерывные функции от аргумента х. Решение линейного уравнения ищут в виде  , где
, где  и
и  – новые неизвестные функции. Подставляя в исходное уравнение
– новые неизвестные функции. Подставляя в исходное уравнение  ,
,  , будем иметь
, будем иметь
 .
.
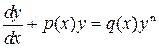
 ,
, .
.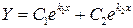 (С 1, С 2 = const)
(С 1, С 2 = const) .
. ,
, ;
; 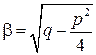 .
.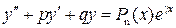 ,
, многочлен степени n может быть представлено в виде
многочлен степени n может быть представлено в виде ,
, – какое-либо частное решение указанного неоднородного уравнения. Для отыскания
– какое-либо частное решение указанного неоднородного уравнения. Для отыскания 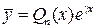 ,
,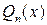 – многочлен степени с неопределенными коэффициентами;
– многочлен степени с неопределенными коэффициентами; ;
; .
. ;
; ;
;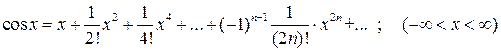 ;
;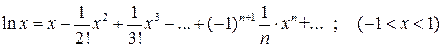 .
. . Если эту функцию продолжить на отрезок
. Если эту функцию продолжить на отрезок  четным образом, то полученное при этом разложение в ряд Фурье будет содержать лишь косинусы кратных дуг и будет представлять данную функцию на заданном отрезке [0, e]. Аналогично поступают, если требуется представить функцию, заданную на отрезке [0, e] тригонометрическим рядом, содержащим лишь синусы кратных дуг.
четным образом, то полученное при этом разложение в ряд Фурье будет содержать лишь косинусы кратных дуг и будет представлять данную функцию на заданном отрезке [0, e]. Аналогично поступают, если требуется представить функцию, заданную на отрезке [0, e] тригонометрическим рядом, содержащим лишь синусы кратных дуг. 403. ху/ + х tg
403. ху/ + х tg  = y
404. xy/ + y ln
= y
404. xy/ + y ln 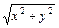 409. xy/ ln
409. xy/ ln 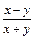
 412. y/ =
412. y/ =  416. y/ =
416. y/ =  417. xy/ = y + 3x sin
417. xy/ = y + 3x sin  .
. обладает свойством
обладает свойством  . Поэтому заданное уравнение является однородным дифференциальным уравнением первого порядка. Совершим замену
. Поэтому заданное уравнение является однородным дифференциальным уравнением первого порядка. Совершим замену 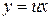 ,
,  . Исходное уравнение приобретает вид
. Исходное уравнение приобретает вид .
. ;
; .
. .
. ;
; .
. ;
; .
.
 .
. ,
, sin x, y
sin x, y  422. y/cos2x + y = tg x, y(0) = -1
423. y/ - y ctg x =
422. y/cos2x + y = tg x, y(0) = -1
423. y/ - y ctg x = 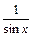 , y
, y 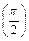 = 0
424. (1 + x2) y/ + y = arctg x, y(0) = 1
425. y/ cos 2x + y = tg x, y (0) = -1
426. y/
= 0
424. (1 + x2) y/ + y = arctg x, y(0) = 1
425. y/ cos 2x + y = tg x, y (0) = -1
426. y/ 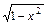 + y = arcsin/x; y(0) = -1
427. (1 + x2)y/ + y = y2 arctg x, y(0) = 1
428. y/ + 2y tg 2x = sin 4x; y(0) = 0
429. xy/ - y = x2 cos x, y
+ y = arcsin/x; y(0) = -1
427. (1 + x2)y/ + y = y2 arctg x, y(0) = 1
428. y/ + 2y tg 2x = sin 4x; y(0) = 0
429. xy/ - y = x2 cos x, y 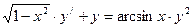 , y(0)=-1
432. xy/ - y = x2 cos x; y(
, y(0)=-1
432. xy/ - y = x2 cos x; y( ) =
) =  433. y/ + 3ytg3x = sin6x, y(0) =
433. y/ + 3ytg3x = sin6x, y(0) = 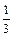 434. xy/ + y = -x2y2; y(1) = 1
435. y/ -
434. xy/ + y = -x2y2; y(1) = 1
435. y/ -  , y(0) = 1
436. y/sin x = - y cos x = 1; y(
, y(0) = 1
436. y/sin x = - y cos x = 1; y( y=x2y2, y(1) = 1
438. y/x + 2y = 3x5y2; y(1) = -1
439. y/ cos2x + y = y2 tg x, y(0) = -1
440. y/ + 2xy = 3x2e
y=x2y2, y(1) = 1
438. y/x + 2y = 3x5y2; y(1) = -1
439. y/ cos2x + y = y2 tg x, y(0) = -1
440. y/ + 2xy = 3x2e  ; y(0) = 0
; y(0) = 0
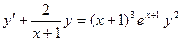 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  .
. , где
, где  – неизвестные функции от х,
– неизвестные функции от х,  ,
,
 так, чтобы выражение, содержащееся в квадратной скобке, обращалось в нуль. Для определения
так, чтобы выражение, содержащееся в квадратной скобке, обращалось в нуль. Для определения  , откуда после интегрирования получаем
, откуда после интегрирования получаем  , т.е.
, т.е. .
.
 .
.


