
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Указания к выполнению контрольной работы № 3Содержание книги
Поиск на нашем сайте
Тема 1. Неопределенный интеграл Прежде чем приступить к интегрированию функций, тщательно изучите таблицу интегралов, простейшие свойства неопределенного интеграла и два простейших метода интегрирования: метод замены переменной и способ подстановки. Успех интегрирования в значительной степени зависит от того, сумеем ли мы подобрать удачную замену переменной упрощающую данный интеграл. При использовании метода интегрирования по частям очень важно правильно выбрать множители u и dv. Хотя общих правил разбиения подынтегрального выражения на указанные множители нет, тем не менее можно руководствоваться некоторыми частными правилами. Например, если подынтегральная функция представляет собой произведение показательной и ли тригонометрической функции и многочлена, то в качестве множителя u следует выбирать многочлен. Если же подынтегральная функция является произведением логарифмической или обратной тригонометрической функции и многочлена, то в качестве множителя u следует выбрать логарифмическую или обратную тригонометрическую функцию. При интегрировании выражения, содержащего в знаменателе квадратный трехчлен, целесообразно привести этот трехчлен к виду с выделенным полным квадратом. При интегрировании рациональных дробей (в задачах № 221‑240) основная трудность заключается в умении интегрировать правильные рациональные дроби следующих трех типов:
Вопросы для самопроверки 1. Сформулируйте определение первообразной. 2. Каковы основные свойства неопределенного интеграла? 3. Укажите целесообразные подстановки для отыскания интегралов:
4. Выведите формулу интегрирования по частям. 5. Объясните правило разложения рациональной дроби на простейшие.
Тема 2. Определенный интеграл При решении задач контрольной работы следует иметь в виду, что для вычисления площади, ограниченной кривыми y = f1(x), y = f2(x), (f1(x)
При этом данная формула остается верной при любых знаках значений функций f1(x), f2(x). При вычислении площади фигуры, ограниченной кривой, уравнение задано в полярных координатах, полезно кривую изобразить в системе координат.
Вопросы для самопроверки 1. Что называется интегральной суммой данной функции f(x) на данном отрезке [ a, b ]? 2. Дайте определение определенного интеграла. 3. Каков геометрический смысл определенного интеграла от заданной функции? 4. Перечислите основные свойства определенного интеграла. 5. Напишите формулу Ньютона – Лейбница. 6. В чем состоит способ подстановки для вычисления определенного интеграла? 7. Как выглядит формула интегрирования по частям для определенного интеграла? 8. Как вычислить площадь криволинейного сектора в полярных координатах? 9. Запишите формулы для вычисления длины дуги кривой в декартовых и в полярных координатах. 10. Приведите формулу для вычисления объема тела с известными площадями его поперечных сечений. 11. Запишите формулу для вычисления объема тела вращения.
КОНТРОЛЬНАЯ РАБОТА № 3 В задачах 161-180 найти неопределенные интегралы способом подстановки (методом замены переменной).
Решение типовых примеров. 1. Найти неопределенный интеграл Решение. Применим подстановку
2. Найти интеграл Решение. Применим подстановку
В задачах 181‑200 найти неопределенные интегралы, используя выделение полного квадрата.
Решение типового примера. Найти интеграл Решение. Преобразуем знаменатель дроби, стоящей под знаком интеграла следующим образом: х2 - 4х + 8 = х2 – 4х + 4 = (х – 2)2 + 22. Тогда после подстановки
При этом при вычислении интеграла
В задачах 201‑220 найти неопределенные интегралы, применяя метод интегрирования по частям.
Решение типовых примеров. 1. Найти интеграл Решение. Применим формулу интегрирования по частям
Положим, что
Найти интеграл Решение. Положим
Применяя в последнем интеграле подстановку следовательно,
Отсюда,
В задачах 221‑240 найти неопределенные интегралы, пользуясь разложением рациональных дробей на простейшие.
Решение типовых примеров. 1. Найти интеграл Решение. Разложим знаменатель на множители: Тогда
Освобождаемся от знаменателя:
Теперь приравниваем коэффициенты при одинаковых степенях х:
х1 1 = А – В + С; х0 0 = А – С; А = С. Из второго уравнения получаем 1 = А + А + А = 3А; А = Отсюда А = Следовательно,
Воспользуемся равенством х2 + х + 1 = х2 + 2* После замены переменной t = x +
Ответ:
2. Найти интеграл Решение. Из равенства
получаем Приравниваем коэффициенты при одинаковых степенях
х1 1 = А – В + С; х0 0 = А – С; А = С. Отсюда А =
В задачах 241‑260 вычислить площадь фигуры, ограниченной заданными параболами.
Решение типового примера. Вычислить площадь, ограниченную параболами (рис. 4)) у = 2х2 – х – 2; у = -х2 + х – 1. Решение. Найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений: 2х2 – х – 2 = -х2 + х – 1. Отсюда 3х2 – 2х – 1 = 0, D = 16, х1 =
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 398; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.21 (0.007 с.) |

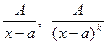 (k – целое положительное число, меньшее, чем 2);
(k – целое положительное число, меньшее, чем 2);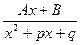 (корни знаменателя невещественные, т.е. p2 - 4q < 0).
(корни знаменателя невещественные, т.е. p2 - 4q < 0).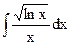 ,
, 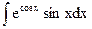 ,
, 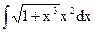 ,
,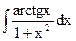 ,
, 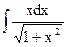 ,
, 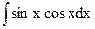 .
.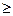 f2(x)) и прямыми х = а, х = b, следует пользоваться формулой:
f2(x)) и прямыми х = а, х = b, следует пользоваться формулой: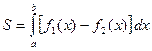 .
.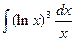
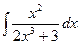
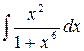
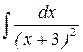
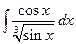
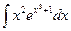
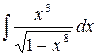
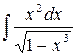
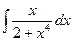
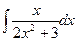
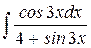

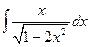
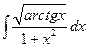
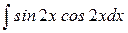

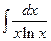
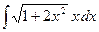
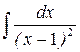
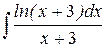
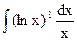 .
.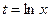 . Тогда
. Тогда 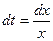 и
и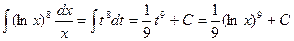 .
. .
.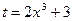 . Тогда
. Тогда 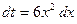 ;
; 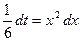 , откуда
, откуда .
.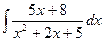 .
182.
.
182. 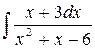 .
183.
.
183. 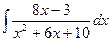 .
184.
.
184.  .
185.
.
185. 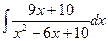 .
186.
.
186. 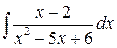 .
187.
.
187. 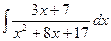 .
188.
.
188. 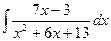 .
190.
.
190.  .
.
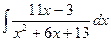 .
192.
.
192. 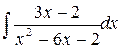 .
193.
.
193. 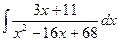 .
194.
.
194. 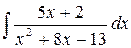 .
195.
.
195. 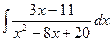 .
196.
.
196. 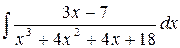 .
197.
.
197. 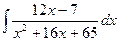 .
198.
.
198. 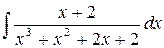 .
199.
.
199. 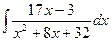 .
200.
.
200. 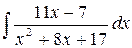 .
.
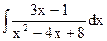 .
.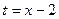 получаем
получаем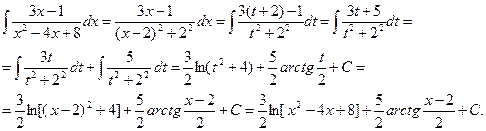
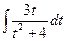 мы воспользовались заменой переменной
мы воспользовались заменой переменной 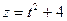 . Тогда
. Тогда 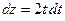 , откуда
, откуда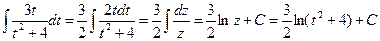 .
. .
202.
.
202. 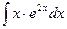 .
203.
.
203. 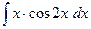 .
204.
.
204. 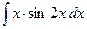 .
205.
.
205. 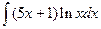 .
206.
.
206. 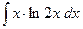 .
207.
.
207. 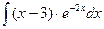 .
208.
.
208. 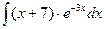 .
209.
.
209.  .
210.
.
210. 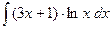 .
.
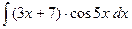 .
212.
.
212. 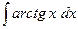 .
213.
.
213. 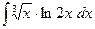 .
214.
.
214. 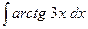 .
215.
.
215. 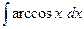 .
216.
.
216. 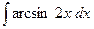 .
217.
.
217. 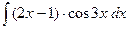 .
218.
.
218. 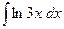 .
219.
.
219. 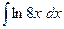 .
220.
.
220. 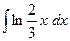 .
.
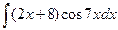 .
.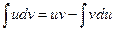 .
.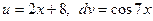 . Тогда
. Тогда 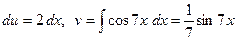 . Следовательно,
. Следовательно,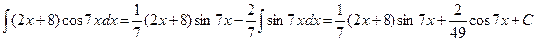
 .
.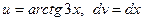 . Тогда
. Тогда 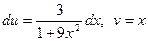 . Отсюда
. Отсюда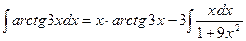 .
.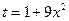 , получаем
, получаем 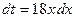 ,
,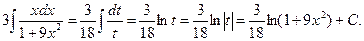
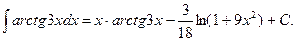
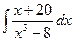 .
222.
.
222. 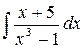 .
223.
.
223. 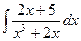 .
224.
.
224. 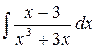 .
.
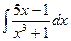 .
232.
.
232. 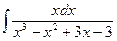 .
233.
.
233. 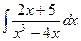 .
234.
.
234. 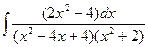 .
.
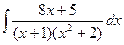 .
226.
.
226. 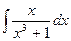 .
227.
.
227. 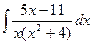 .
228.
.
228. 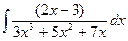 .
229.
.
229. 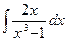 .
230.
.
230. 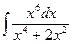 .
.
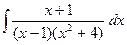 .
236.
.
236. 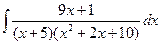 .
237.
.
237. 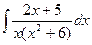 .
238.
.
238. 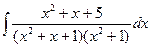 .
239.
.
239. 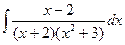 .
240..
.
240.. 
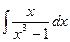 .
.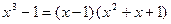 .
.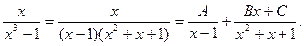
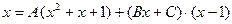 .
. х2 0 = А + В; А = -В;
х2 0 = А + В; А = -В;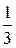 .
.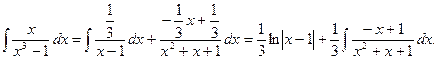
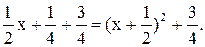
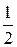 , dt = dx, x = t -
, dt = dx, x = t - 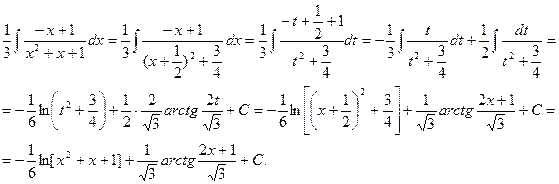
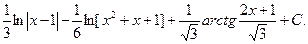
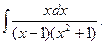
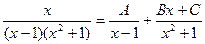
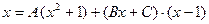 .
.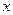 :
: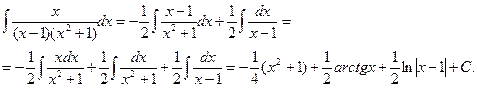
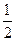 х2 + х + 2
у= -
х2 + х + 2
у= -  + 2х + 9
+ 2х + 9
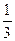 х2 + 2х – 2
у = -
х2 + 2х – 2
у = - 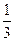 х2 – 2х + 4
у= -
х2 – 2х + 4
у= -  х2 – х + 2
х2 – х + 2
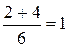 , х2 =
, х2 = 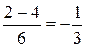 .
.


