
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Указания к выполнению контрольной работы № 2Содержание книги
Поиск на нашем сайте
Тема 1. Введение в анализ. Функция одной переменной
При изучении этой темы обратите внимание на понятие функции, способы задания функции, основные элементарные функции. Центральными понятиями в этой теме являются понятия предела переменной величины, предела функции и понятие непрерывной функции. При решении задач на вычисление пределов функции обратите внимание на то, что в определении предела функции не учитывается значение функции в предельной точке, другими словами, величина
Вопросы для самопроверки
1. Что такое переменная величина? 2. Сформулируйте определение функции. Что называется областью определения функции? 3. Какие способы задания функции Вы знаете? 4. Какие функции называются элементарными? 5. Сформулируйте понятие предела переменной величины. 6. Дайте определение понятия предела функции. 7. Какая функция называется ограниченной? 8. В каком случае функция называется бесконечно малой? 9. Сформулируйте основные теоремы о пределах. 10. Дайте определение непрерывности функции в точке. 11. Укажите основные свойства непрерывных функций.
Тема 2. Производная и дифференциал
При изучении этой темы обратите внимание на определение производной, ее геометрическое и механическое истолкование. Особую роль при решении задач играет правило вычисления производной сложной функции. При дифференцировании некоторых функций нередко значительно упрощает вычисление прием, состоящий в том, что перед вычислением производной функцию предварительно логарифмируют.
Вопросы для самопроверки
1. Сформулируйте определение производной. 2. Каков геометрический смысл производной? 3. Что называется касательной к кривой? Напишите уравнение касательной к графику функции y = f (x). 4. Каков механический смысл первой и второй производной?
5. Каковы правила вычисления производных от суммы, произведения, частного двух функций? 6. Сформулируйте правило вычисления производной сложной функции. 7. Что называется дифференциалом функции? 8. Чем отличается дифференциал функции от ее приращения?
Тема 3. Исследование поведения функций Изучение этой темы следует начать с усвоения понятий возрастания и убывания функции, максимума и минимума функции, выпуклости и вогнутости кривой. Обратите внимание на следующие обстоятельства: 1) функция, определенная на отрезке, может достигать максимума и минимума только при значениях x, заключенных внутри рассматриваемого отрезка; 2) не следует считать, что максимум и минимум функции являются соответственно ее наибольшим и наименьшим значениями на рассматриваемом отрезке (например, в точке максимума функция имеет наибольшее значение лишь по сравнению с теми значениями, которые она имеет во всех точках, достаточно близких к точке максимума). При решении задач на построение графика функции следует учесть, что приведенный в формулировке задач № 121‑140 порядок исследования функций может быть нарушен, так знание одних свойств функции позволяет сделать вывод о других ее свойствах. Так, например, если при исследовании точек разрыва функции выяснено, что односторонние пределы функции в некоторой точке бесконечны, то это означает наличие в этой точке вертикальной асимптоты графика. Иногда целесообразно намечать элементы графика параллельно с исследованием функции.
Вопросы для самопроверки
1. Как формулируется теорема Лагранжа? 2. Каковы признаки возрастания и убывания функции? 3. Докажите, что функция y = cos x – x убывает в любом промежутке. 4. Сформулируйте правила нахождения экстремумов функции. 5. Приведите пример, показывающий, что обращение в нуль производной не является достаточным условием экстремума функции. 6. Как найти интервалы выпуклости, вогнутости, точки перегиба кривой? 7. Покажите, что график функции 8. Дайте определение асимптоты кривой. Как найти вертикальные и наклонные асимптоты графика функции?
|
|||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.95.31 (0.01 с.) |

 не зависит от величины f (a). Значение f (a) может и не существовать. Отсюда следует, что под знаком предела можно производить тождественные преобразования выражения, не принимая во внимание его поведение в предельной точке. В частности, под знаком пределов можно производить сокращение дроби на множитель, обращающийся в нуль в предельной точке (но не равный нулю вблизи этой точки).
не зависит от величины f (a). Значение f (a) может и не существовать. Отсюда следует, что под знаком предела можно производить тождественные преобразования выражения, не принимая во внимание его поведение в предельной точке. В частности, под знаком пределов можно производить сокращение дроби на множитель, обращающийся в нуль в предельной точке (но не равный нулю вблизи этой точки).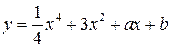 не имеет точек перегиба, каковы бы ни были значения a и b.
не имеет точек перегиба, каковы бы ни были значения a и b.


