
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Применение правил отыскания наибольшихСодержание книги
Поиск на нашем сайте
И наименьших значений к решению задач
При решении задач этой темы следует иметь в виду, что наибольшее и наименьшее значения функция достигает либо на концах заданного отрезка, либо в тех его внутренних точках, которые являются критическими точками первого рода этой функции (точками, подозрительными на экстремум).
Контрольная работа № 2 В задачах 61 – 80 найти указанные пределы.
Решение типовых примеров. 1) 2) При подстановке вместо переменной х ее предельного значения 3 получается неопределенность вида ax 2 + bx + c = a (x – x 1)(x – x 2), где х 1, х 2 – корни квадратного трехчлена ax 2 + bx + c. У нас 2 х 2 – 3 х – 9 = 2(х – 3)(х + так как дискриминант квадратного трехчлена D = 9 – 4 · 2 · (– 9) = 81, а следовательно, х 1 = 3, х 2 = – Аналогично х 2 – х – 6 = (х – 3)(х + 2) Теперь условие примера можно переписать в другом виде и продолжить решение:
3) Здесь сталкиваемся с неопределенностью
4) В данном случае для освобождения от неопределенности будем использовать первый замечательный предел и одно из его очевидных следствий:
Решение примера будет выглядеть следующим образом:
В задачах 81‑100 найти производные
Решение типовых примеров. При решении всех последующих примеров кроме таблицы производных будут использованы известные правила дифференцирования суммы, разности, произведения, дроби и теорема о производной сложной функции: а) [ f (x) ± φ(x)]΄ = f ΄(x) ± φ΄(x); б) [ f (x) · φ(x)]΄ = f ΄(x)φ(x) + f (x)φ΄(x); в) г) если задана сложная функция y = f (u), где u = φ(x), то есть y = f (φ(x)); если каждая из функций y = f (u) и u = φ(x) дифференцируема по своему аргументу, то
1)
2)
3)
4)
В задачах 101 – 120 задан закон s (t) изменения пути движения материальной точки. Требуется найти значения скорости и ускорения этой точки в момент времени t 0. 101. 102. 103. 104. 105. 106. 107. 108. 109. 110. 111. 112. 113. 114. 115. 116. 117. 118. 119. 120.
Решение типового примера. Пусть s (t) = 3 x 4 – 2 x 3 + x – 1, t 0 = 2. Известно, что значения скорости и ускорения материальной точки в некоторый момент времени являются соответственно значениями в этот момент первой и второй производных функции, задающей закон изменения пути движения точки. У нас
в задачах 121‑140 исследовать заданные функции методами дифференциального исчисления, начертить их графики. Исследование функций и построение графиков рекомендуется проводить по следующей схеме: 1) найти область определения функции D(y); 2) исследовать функцию на непрерывность; найти точки разрыва функции, ее односторонние пределы в точках разрыва; 3) найти точки экстремума функции и определить интервалы ее монотонности; 4) найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика; 5) найти асимптоты графика функции; 6) построить график, используя результаты предыдущих исследований; 7) для функции из пункта а) найти дополнительно наибольшее и наименьшее значения на отрезке [α; β].
Решение типовых примеров. 1. 1) Областью определения данной функции являются все действительные значения аргумента x, то есть 2) Исследуем функцию на экстремум и интервалы монотонности. С этой целью найдем ее производную и приравняем ее к нулю:
Решая полученное квадратное уравнение, делаем вывод о том, что функция имеет две критические точки 1 рода x 1 = – 5, x 2 = – 1. Разбиваем область определения этими точками на части и по изменению знака производной в них выявляем промежутки монотонности и наличие экстремума:
3) Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем вторую производную заданной функции и приравняем ее к нулю:
Итак, функция имеет одну критическую точку 2 рода х = – 3. Разобьем область определения полученной точкой на части, в каждой из которых установим знак второй производной:
Значение х = – 3 является абсциссой точки перегиба графика функции, а ордината этой точки
4) Выясним наличие у графика заданной функции наклонных асимптот. Для определения параметров уравнения асимптоты
Имеем
Таким образом, у графика заданной функции наклонных асимптот нет.
Рис. 2
5) Для построения графика в выбранной системе координат изобразим точки максимума А 1(– 5; 4), минимума А 2(– 1; 4), перегиба А 3(0; 6) Найдем наибольшее и наименьшее значения заданной функции на отрезке [– 3; 0]. Для этого посчитаем значения функции на концах этого отрезка, в критических точках 1 рода, попавших на отрезок, и сравним результаты: y (– 3) = 0; y (– 1) = – 4; y (0) = – Очевидно,
2. 1) Область определения.
2) Исследование на непрерывность и классификация точек разрыва. Заданная функция непрерывна всюду, кроме точки х = 4. Вычислим ее односторонние пределы в этой точке:
Таким образом, точка х = 4 является для заданной функции точкой разрыва второго рода, а прямая х = 4 – вертикальной асимптотой графика. 3) Исследование на экстремум и промежутки монотонности.
х 1 = – 2, х 2 = 10.
4) Исследование графика на выпуклость, вогнутость, точки перегиба.
Так как
5) Исследование графика на наличие наклонных асимптот.
Таким образом, прямая 6) Построение графика. Очевидно, график заданной функции пересекает ось Оу в точке (0; –5) и на основе обобщения результатов всех предыдущих исследований имеет вид, представленный на рис. 3.
Рис. 3
141. Каковы должны быть размеры прямоугольника наибольшей площади, вписанного в круг радиуса 6 см? 142. Проволока длиной 40 см согнута в прямоугольник. Каковы должны быть размеры этого прямоугольника, чтобы его площадь была наибольшей? 143. Канал, ширина которого 27 м, под прямым углом впадает в другой канал шириной 64 м. Какова наибольшая длина бревен, которые можно сплавить по этой системе каналов? 144. Найти наибольший объем цилиндра, у которого полная поверхность равна 145. Найти наибольший объем конуса, образующая которого равна 146. Турист идет из пункта А, находящегося на шоссейной дороге, в пункт В, расположенный в 8 км от шоссе. Расстояние от А до В по прямой составляет 17 км. В каком месте туристу следует свернуть с шоссе, чтобы в кратчайшее время прийти в пункт В, если его скорость передвижения по шоссе 5 км/ч, а по бездорожью 3 км/ч? 147. Объем правильной треугольной призмы равен 148. Открытый чан имеет форму цилиндра объема 149. Требуется изготовить коническую воронку с образующей, равной 20 см. Какова должна быть высота воронки, чтобы ее объем был наибольшим? 150. Требуется изготовить ящик с крышкой, объем которого был бы равен 72 (см 151. Сечение оросительного канала имеет форму равнобедренной трапеции, боковые стороны которой равны меньшему основанию. При каком угле наклона боковых сторон сечение канала будет иметь наибольшую площадь? 152. Требуется изготовить полотняный шатер, имеющий форму прямого кругового конуса заданной вместимости 153. Из прямоугольного листа жести размером 24 154. Найти треугольник наибольшей площади, если сумма длин его катета и гипотенузы постоянна и равна 4 см. 155. Число 8 разбить на два таких слагаемых, чтобы сумма их квадратов была наименьшей. 156. Число 8 разбить на два таких слагаемых, чтобы сумма их кубов была наименьшей.
157. Какое положительное число, будучи сложенным с обратным ему числом, дает наименьшую сумму? 158. Деталь из листового железа имеет форму равнобедренного треугольника с боковой стороной 10 см. Каким должно быть основание треугольника, чтобы его площадь была наибольшей? 159. Огород прямоугольной формы огорожен изгородью, длина которого 72 м. Каковы должны быть размеры огорода, чтобы его площадь была максимальной? 160. Требуется огородить забором прямоугольный участок земли площадью 294 м
Решение типовой задачи. Задача. Среди цилиндров, полная поверхность которых равна S = 6π (м2), найти цилиндр, имеющий наибольший объем. Решение. Пусть радиус основания цилиндра равен x, а высота равна y. Тогда
откуда
Исследуем полученную функцию на максимум при x > 0. Имеем Так как при
поэтому искомые значения радиуса основания и высоты цилиндра равны соответственно 1 и 2.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 516; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.119.139 (0.012 с.) |

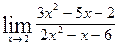 ;
;
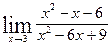 ;
;
 .
.
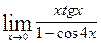 .
.
 ;
;
 ;
;
 .
.
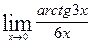 .
.
 ;
;
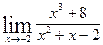 ;
;
 .
.
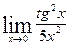 .
.
 ;
;
 ;
;
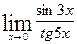 .
.
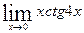 .
.
 ;
;
 ;
;
 .
.
 .
.
 ;
;
 ;
;
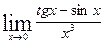 .
.
 .
.
 ;
;
 ;
;
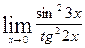 .
.
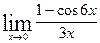 .
.
 ;
;
 ;
;
 .
.
 .
.
 ;
;
 ;
;
 .
.
 .
.
 ;
;
 ;
;
 .
.
 .
.
 .
. .
. . Для избавления от этого типа неопределенности в нашем случае представим квадратные трехчлены числителя и знаменателя в виде произведения линейных множителей, воспользовавшись известной формулой
. Для избавления от этого типа неопределенности в нашем случае представим квадратные трехчлены числителя и знаменателя в виде произведения линейных множителей, воспользовавшись известной формулой ),
), .
. .
. , избавиться от которой можно вынесением за скобки в числителе и знаменателе дроби старшей степени переменной:
, избавиться от которой можно вынесением за скобки в числителе и знаменателе дроби старшей степени переменной: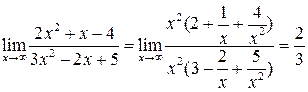 .
. .
. .
. .
. , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования. ;
;
 ;
;
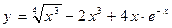 ;
;
 .
.
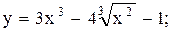
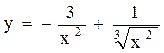 ;
;
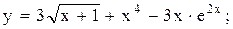
 .
.
 ;
;
 ;
;
 ;
;
 .
.
 ;
;
 ;
;
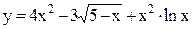 ;
;
 .
.
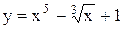 ;
;
 ;
;
 ;
;
 .
.
 ;
;
 ;
;
 ;
;
 .
.
 ;
;
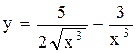 ;
;

 .
.
 ;
;
 ;
;
 ;
;
 .
.
 ;
;
 ;
;
 ;
;
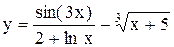 .
.
 ;
;
 ;
;
 ;
;
 .
.
 ;
;
 ;
;
 ;
;
 .
.
 ;
;
 ;
;
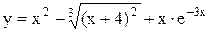 ;
;
 .
.
 ;
;
 ;
;
 ;
;
 .
.
 ;
;
 ;
;
 ;
;
 .
.
 ;
;
 ;
;

 .
.
 ;
;
 ;
;
 ;
;
 .
.

 ;
;
 ;
;
 ;
;
 .
.
 ;
;
 ;
;
 ;
;

 ;
;
 ;
;
 ;
;
 .
.
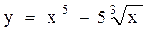 ;
;
 ;
;
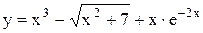 ;
;
 .
.
 ;
; .
.

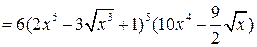 .
. ;
;
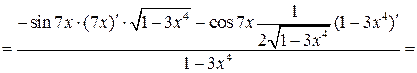
 .
.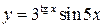 ;
; .
. ;
; .
. .
.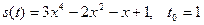 .
. .
. .
. .
.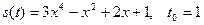 .
. .
. .
. .
.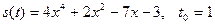 .
. .
. .
. .
. .
. .
.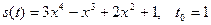 .
. .
. .
. .
. .
. (ед. скор.),
(ед. скор.), (ед. ускор.).
(ед. ускор.).

 .
.


 .
.


 .
.

 .
.


 .
.


 .
.


 .
.


 .
.


 .
.


 .
.


 .
.


 .
.


 .
.

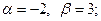
 .
.


 .
.


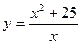 .
.

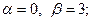
 .
.


 .
.


 .
.

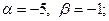
 .
.
 .
.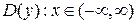 , а это значит, что функция непрерывна на всей числовой прямой и ее график не имеет вертикальных асимптот.
, а это значит, что функция непрерывна на всей числовой прямой и ее график не имеет вертикальных асимптот. .
.




 .
.


 .
. воспользуемся формулами
воспользуемся формулами


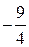 ). С учетом результатов предыдущих исследований построим кривую (см. рис. 2).
). С учетом результатов предыдущих исследований построим кривую (см. рис. 2). .
.
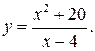

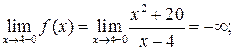




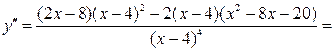
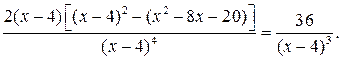
 , то график заданной функции точек перегиба не имеет. Остается выяснить вопрос об интервалах его выпуклости и вогнутости:
, то график заданной функции точек перегиба не имеет. Остается выяснить вопрос об интервалах его выпуклости и вогнутости:

 – наклонная асимптота графика.
– наклонная асимптота графика.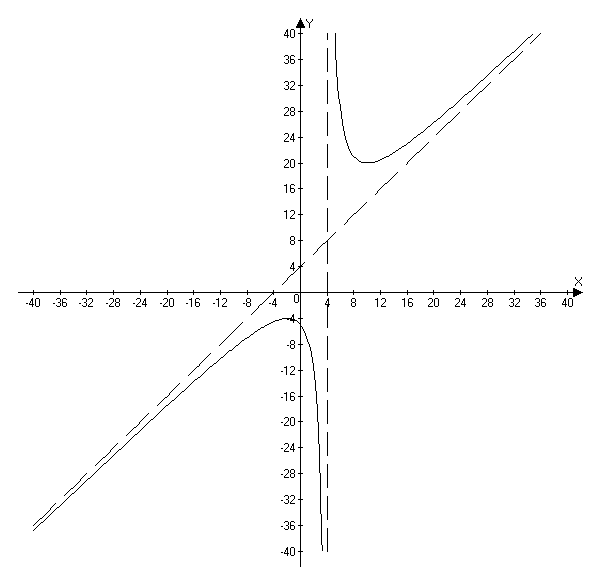
 .
. (м).
(м). . Какова должна быть длина основания призмы, чтобы ее полная поверхность была наименьшей?
. Какова должна быть длина основания призмы, чтобы ее полная поверхность была наименьшей? . Каковы должны быть радиус основания и высота чана, чтобы на его изготовление ушло наименьшее количество материала?
. Каковы должны быть радиус основания и высота чана, чтобы на его изготовление ушло наименьшее количество материала? ), причем стороны основания относились бы как 1:2. Каковы должны быть размеры сторон ящика, чтобы его полная поверхность была наименьшей?
), причем стороны основания относились бы как 1:2. Каковы должны быть размеры сторон ящика, чтобы его полная поверхность была наименьшей? (м
(м  9 см требуется изготовить открытую коробку, вырезая по углам листа равные квадраты и загибая оставшиеся боковые полосы под прямым углом. Какова должна быть сторона вырезаемых квадратов, чтобы вместимость коробки была наименьшей?
9 см требуется изготовить открытую коробку, вырезая по углам листа равные квадраты и загибая оставшиеся боковые полосы под прямым углом. Какова должна быть сторона вырезаемых квадратов, чтобы вместимость коробки была наименьшей? и разделить затем этот участок забором на две равные части. При каких линейных размерах участка длина всего забора будет наименьшей?
и разделить затем этот участок забором на две равные части. При каких линейных размерах участка длина всего забора будет наименьшей? ,
, , то есть объем цилиндра может быть выражен следующим образом:
, то есть объем цилиндра может быть выражен следующим образом: .
. при
при 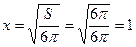 .
. выполняется условие
выполняется условие  то объем имеет наибольшее значение. При этом
то объем имеет наибольшее значение. При этом



