
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Указания к выполнению контрольной работы № 6Содержание книги
Поиск на нашем сайте
Для решения задач по этой теме необходимо уделить особое внимание следующим вопросам: 1) правила сложения и умножения вероятностей и некоторые следствия из них (вероятность появления только одного из независимых в совокупности событий; вероятность появления хотя бы одного из независимых в совокупности событий); 2) математическое ожидание и дисперсия дискретной случайной величины, их свойства (в частности, математическое ожидание и дисперсия для суммы двух случайных величин); 3) функция распределения и плотность распределения вероятностей для непрерывной случайной величины; нахождение вероятности попадания случайной величины в заданный интервал; нахождение числовых характеристик непрерывной случайной величины; 4) нормальное распределение, вероятность попадания нормально распределенной случайной величины в заданный интервал; 5) построение доверительных интервалов для параметров нормально распределенной случайной величины.
Вопросы для самопроверки
1. Сформулируйте классическое определение вероятности события. 2. Сформулируйте теоремы сложения и умножения вероятностей. 3. Дайте определение полной группы событий. 4. Какие случайные величины называют дискретными (непрерывными)? 5. Каковы свойства математического ожидания и дисперсии случайной величины? 6. Запишите различные формулы для вычисления дисперсии случайной величины. 7. Как связаны функция распределения и плотность распределения вероятностей случайной величины? 8. Как найти вероятность попадания случайной величины в заданный интервал? 9. Какая случайная величина называется нормально распределенной? 10. Что такое «правило 3 11. Напишите формулы для вычисления выборочных числовых характеристик. 12. Как найти доверительный интервал для математического ожидания нормально распределенной случайной величины (при известном 13. Как найти доверительный интервал для среднего квадратического отклонения нормально распределенной случайной величины?
КОНТРОЛЬНАЯ РАБОТА № 6
В задачах 521 – 540 найти вероятности указанных событий, пользуясь правилами сложения и умножения вероятностей. 521. Студент знает 45 из 60 вопросов программы. Каждый экзаменационный билет содержит три вопроса. Найти вероятности того, что студент знает все три вопроса. 522. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что наугад взятое изделие окажется бракованным, равна,15. Проверено три изделия. Какова вероятность того, что два из них бракованные? 523. В электрическую цепь включены последовательно три элемента, работающие независимо друг от друга. Вероятность отказа 1-го, 2-го и 3-го элементов соответственно равны р1 = 0,1, р2 = 0,15, р3 = 0,2. Найти вероятность того, что в цепи не будет отказа. 524. В ящике имеется 12 деталей, из которых 5 деталей нестандартны. Сборщик наудачу извлекает из ящика 4 детали. Какова вероятность того, что все они будут нестандартны? 525. В двух ящиках находятся детали, в первом – 10 (их них 3 нестандартных), во втором – 15 (из них 6 нестандартных). Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что обе детали окажутся стандартными. 526. Техническое устройство содержит три независимо работающих элемента. Вероятности отказа этих элементов соответственно равны 0,05; 0,07 и 0,09. Найти вероятность того, что техническое устройство не сработает, если для этого достаточно, чтобы отказал хотя бы один элемент. 527. Стрелок стреляет в мишень, разделенную на 3 области. Вероятность попадания в первую область равна 0,45, во вторую – 0,35. Найти вероятность того, что стрелок при одном выстреле, попадает либо в первую, либо во вторую область. 528. Вероятность попадания в мишень при трех выстрелах хотя бы один раз для некоторого стрелка равна 0,875. Найти вероятность попадания при одном выстреле. 529. В каждой из двух урн находится 5 белых и 10 черных шаров. Из первой урны во вторую переложили 1 шар, а затем из второй урны вынули один шар. Найти вероятность того, что вынутый из второй урны шар окажется черным. 530. Исследователь разыскивает нужные ему сведения в трех справочниках. Вероятность того, что эти сведения находятся в первом, во втором и в третьем справочнике равны соответственно 0,7; 0,6; 0,9. Найти вероятность того, что требуемые сведения содержатся хотя бы в одном справочнике. 531.Батарея из трех орудий производит залпы, причем 2 снаряда попадают в цель. Найти вероятность того, что первое орудие дало попадание, если вероятность попадания в цель 1-го, 2-го и 3-го орудий соответственно равны 0,4; 0,3; 0,5. 532.В первом ящике 2 белых и 10 черных шаров. Во втором ящике 8 белых и 4 черных шара. Из каждого ящика наудачу вынули по шару. Какова вероятность, что оба шара белые? 533.Предприятие изготавливает 95% деталей стандартных, причем 86 из них – первого сорта. Найти вероятность того, что взятое наудачу изделие, изготовленное на этом предприятии, окажется первого сорта. 534.В урне 20 шаров, из которых 7 красных, а остальные белые. Наудачу вынули три шара. Какова вероятность, что все они белые? 535.В урне 5 белых и 4 черных шара. Из урны извлекают сразу 3 шара. Найти вероятность того, что хотя бы один шар был черным. 536.В группе из 18 студентов имеется 5 отличников. Выбираются наудачу три студента. Какова вероятность, что все они отличники? 537.Две перфораторщицы набили по одинаковому количеству перфокарт. Вероятность того, что первая перфораторщица допустила ошибку, равна 0,05; вторая – 0,1. При сверке перфокарт была обнаружена ошибка. Найти вероятность того, что ошиблась первая перфораторщица. 538.Имеются два ящика, в первом из которых 5 белых и 8 красных шаров, а во втором – 3 белых и 2 красных шара. какова вероятность того, что один из них будет красным, а другой белым? 539.В мешочке имеется 6 букв разрезной азбуки А, А, Б, Б, Б, О. Их достают из мешочка по одной и раскладывают в «одну линию». Найти вероятность того, что по этим буквам можно прочитать слово «БАОБАБ». 540.Вероятность обнаружения цели при одном цикле обзора радиолокационной станцией равна 0,3. Какова вероятность обнаружения цели хотя бы один раз при четырех циклах обзора?
Решение типовых задач. 1. Три стрелка производят по одному выстрелу в цель независимо друг от друга. Вероятности попадания каждого из них равны соответственно 0,7; 0,8; 0,9. найти вероятность того, что: а) в цель попадет только один стрелок; б) в цель попадут только два стрелка; в) в цель попадет хотя бы один стрелок. Решение. а) Рассмотрим следующие события: А1 – первый стрелок попал в цель; А2 – второй стрелок попал в цель; А3 – третий стрелок попал в цель;
По условию Р(А1)=0,7; Р(А2)=0,8; Р(А3)=0,9; Р( Пусть событие В – попал только один стрелок. Тогда В = А1 Отсюда в силу несовместности событий-слагаемых и независимости событий-сомножителей Р(В) = Р(А1) = 0,7 б) Пусть событие С – попадут только два стрелка. Тогда С = А1 Отсюда Р(С) = 0,7 в) Пусть событие D – попал хотя бы один стрелок. Тогда противоположное событие Поэтому Р( Р(D) = 1 – Р(D) = 1 – 0,006 = 0,994.
2. Среди 15 микрокалькуляторов, имеющихся в вычислительной лаборатории, лишь 6 новых, а остальные – бывшие в употреблении. Наугад взято три микрокалькулятора. Какова вероятность, что все они окажутся новыми? Решение. Рассмотрим события: А – первый из взятых микрокалькуляторов новый; В – второй микрокалькулятор новый; С – третий микрокалькулятор новый. Тогда Р(А) = Вероятность того, что второй микрокалькулятор будет новый, при условии, что первым уже был отобран новый микрокалькулятор, т.е. условная вероятность события В, равна РА (В) = Вероятность того, что третьим будет отобран новый микрокалькулятор, при условии, что уже отобраны два новых микрокалькулятора, т.е. условная вероятность события С, равна Р АВ (С) = Искомая вероятность того, что все три отобранных микрокалькулятора окажутся новыми, равна Р(АВС) = Р(А)
В задачах 541 ‑ 560 две независимые дискретные величины Х и У заданы своими законами распределения. Найти математическое ожидание и дисперсию для случайной величины Z = 2X – 5Y.
541.
542.
543.
544.
545.
546.
547.
548.
549.
550.
551.
552.
553.
554.
555.
556.
557.
558.
559.
560.
Решение типового примера. Заданы законы распределения двух независимых случайных величин Х и У
Найти математическое ожидание и дисперсию для случайной величины Z = 2X – 7Y. Решение. Найдем математические ожидания и дисперсии для случайных величин Х и У. М(Х) = -5 М(У) = 1 Напишем законы распределения для случайных Х2 и У2:
Найдем математические ожидания для случайных величин Х2 и У2: М(Х2) = 25 М(У2) = 1 Отсюда D(X) = М(Х2) – [M(X)]2 = 15,3 – (-0,3)2 = 15,21; D(Y) = M(Y2) – [M(Y)]2 = 13,0 – (3,4)2 = 1,44. Наконец, пользуясь свойствами математического ожидания и дисперсии, а также независимостью случайных величин Х и У, получаем М(Z) = M(2X – 7Y) = 2M(X) – 7M(Y) = 2 D(Z) = D(2X – 7Y) = 4D(X) + 49D(Y) = 4
В задачах 561 ‑ 580 случайная величина Х задана функцией распределения вероятностей F(x). Найти: а) вероятность попадания случайной величины Х в интервал
561.
562.
563.
564.
565.
566.
567.
568.
569.
570.
571.
572.
573.
574.
575.
576.
577.
578.
579.
580.
Решение типового примера. Случайная величина Х задана функцией распределения вероятностей
Найти: а) вероятность попадания случайной величины Х в интервал Решение. а) Вероятность того, что случайная величина Х примет значение, заключенное интервале Р б) Найдем плотность распределения вероятностей случайной величины Х по формуле
Получаем
в) Математическое ожидание случайной величины Х находим по формуле
Имеем
В задачах 581 ‑ 600 предполагается, что случайные отклонения контролируемого размера детали, изготовленной станком-автоматом, от проектного размера подчиняются нормальному закону распределения со средним квадратическим отклонением
Решение типового примера. Станок-автомат изготавливает шарики. Шарик считается годным, если отклонение Решение. Воспользуемся формулой для вычисления вероятности заданного отклонения от нормально распределенной случайной величины
где По условию задачи
Таким образом, станок-автомат изготавливает 92,8% годных шариков.
В задачах 601 – 620 известно, что проведено n равноточных измерений некоторой физической величины и найдено среднее арифметическое результатов измерений
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 557; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.142.113 (0.01 с.) |

 »?
»? - первый стрелок не попал в цель;
- первый стрелок не попал в цель; - второй стрелок 6е попал в цель;
- второй стрелок 6е попал в цель; - третий стрелок не попал в цель.
- третий стрелок не попал в цель. Р(
Р( - не попал ни один стрелок из них, т.е.
- не попал ни один стрелок из них, т.е.  .
. .
. .
. .
. б) плотность распределения вероятностей случайной величины Х; в) математическое ожидание случайной величины Х.
б) плотность распределения вероятностей случайной величины Х; в) математическое ожидание случайной величины Х.







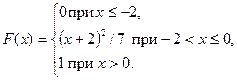











 б) плотность распределения вероятностей случайной величины Х; в) математическое ожидание случайной величины Х.
б) плотность распределения вероятностей случайной величины Х; в) математическое ожидание случайной величины Х. = F(-
= F(-  ) – F(-
) – F(-  ) =
) =  (-
(-  .
. .
.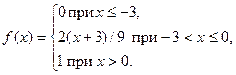
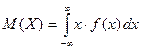 .
. .
. его диаметра от проектного размера по абсолютной величине меньше 0,9 мм. Считая, что случайная величина
его диаметра от проектного размера по абсолютной величине меньше 0,9 мм. Считая, что случайная величина  мм, найти, сколько процентов годных шариков изготавливает станок-автомат.
мм, найти, сколько процентов годных шариков изготавливает станок-автомат. ,
, – функция Лапласа (см. приложение 1).
– функция Лапласа (см. приложение 1). , поэтому
, поэтому .
.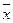 . Все измерения проведены одним и тем же прибором с известным средним квадратическим отклонением ошибок измерений. Считая результаты измерений нормально распределенной случайной величиной, найти с надежностью
. Все измерения проведены одним и тем же прибором с известным средним квадратическим отклонением ошибок измерений. Считая результаты измерений нормально распределенной случайной величиной, найти с надежностью 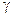 доверительный интервал для оценки истинного значения измеряемой физической величины.
доверительный интервал для оценки истинного значения измеряемой физической величины.


