Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Определители. Решение систем линейных уравненийСодержание книги
Поиск на нашем сайте
Знакомство с использованием определителей начните с простейшего случая решения и исследования системы двух линейных уравнений с двумя неизвестными. Изучите свойства определителей второго, а затем третьего порядка. Особое внимание обратите внимание на то, что вычисление определителей часто упрощается, если умело пользоваться свойствами определителей. При изучении вопросов, связанных с исследованием систем линейных уравнений, не упустите из виду случай, когда определитель системы равен нулю. В этой ситуации формулы Крамера теряют смысл и соответствующие системы уравнений либо несовместны, либо имеют бесчисленное множество решений.
Вопросы для самопроверки 1. Перечислите свойства определителей. 2. Какие способы вычисления определителей вы знаете? 3. Какой вид имеют формулы Крамера? В каком случае их можно применять? 4. Сформулируйте условие, при котором система линейных уравнений имеет единственное решение. 5. При каком условии система линейных однородных уравнений имеет ненулевое решение? Тема 2. Элементы аналитической геометрии на плоскости При изучении этой темы, прежде всего, следует усвоить понятие уравнения линии. Подобно тому, как точка в аналитической геометрии определяется числами (координатами точки), линия определяется уравнением, связывающим координаты любой точки этой линии (уравнением линии). Прямая линия является простейшей из линий на плоскости. Изучите различные способы нахождения уравнения прямой. Успех решения задач, связанных с прямыми на плоскости, во многом зависит от умелого выбора соответствующего вида уравнения прямой.
Вопросы для самопроверки 1. Как определяются декартовы координаты точки на плоскости. 2. Чем отличаются координаты двух точек, симметричны относительно: а) оси Ox; б) оси Oy; в) начала координат? 3. Как вычислить расстояние между двумя точками? 4. Напишите формулы для координат середины отрезка через координаты его концов. 5. Напишите формулы для координат точки пересечения медиан треугольника через координаты его вершин. 6. Дайте определение уравнения линии на плоскости. 7. Как найти координаты точки пересечения двух линий на плоскости, заданных своими уравнениями?
8. Чем отличается уравнение прямой в декартовых координатах от уравнений других линий? 9. Напишите формулу для вычисления угла между двумя прямыми. 10. Как выглядит условие параллельности и перпендикулярности двух прямых. 11. Напишите уравнение прямой, проходящей: а) через заданную точку в заданном направлении; б) через две заданные точки. 12. Как написать уравнение медианы, высоты в треугольнике, если известны координаты его вершин? 13. Сформулируйте определения эллипса, гиперболы, параболы. Каковы канонические уравнения этих линий? 14. Что называется эксцентриситетом эллипса и гиперболы и какие значения он может иметь для каждой из этих линий?
Тема 3. Элементы векторной алгебры и аналитической геометрии в пространстве
В основе этой темы лежит понятие вектора и его координат на плоскости и в пространстве. Узловыми моментами являются действия с векторами: сложение и вычитание векторов, умножение вектора на число, скалярное и векторное умножение двух векторов, смешанное произведение трёх векторов. Особое внимание следует обратить на непростое определение векторного произведения векторов и на область применения каждого вида произведений векторов при решении задач геометрии (вычислении углов, площадей, объёмов). После подробного изучения элементов векторной алгебры следует перейти к обсуждению вопросов, связанных с составлением уравнений плоскости и прямой в пространстве.
Вопросы для самопроверки 1. Как определяется сумма и разность двух векторов? 2. Дайте определение коллинеарных и компланарных векторов. 3. Дайте определение проекции вектора на ось. 4. Как выглядит разложение вектора в системе орт на плоскости и в пространстве? Что такое координаты вектора? 5. Каковы свойства скалярного произведения векторов? 6. Как найти угол между векторами? Как найти длину вектора по его координатам? 7. Каково условие перпендикулярности двух векторов? 8. Как найти вектор, перпендикулярный двум данным векторам? 9. Как найти площадь треугольника, построенного на двух векторах? 10. Как найти объём пирамиды с вершинами в заданных точках? 11. Как выглядит условие компланарности трёх векторов? 12. Что Вы можете сказать о соответственных координатах двух коллинеарных векторов?
13. Как выглядит уравнение плоскости, проходящей: а) через заданную точку с заданным нормальным вектором; б) через три заданные точки? 14. Напишите формулу для вычисления угла между двумя плоскостями. 15. Какие Вы знаете виды уравнений прямой в пространстве? 16. Как выглядит формула для отыскания угла между двумя прямыми в пространстве. 17. Как найти координаты точки пересечения плоскости и прямой? 18. Как найти расстояние от заданной точки до заданной плоскости? КОНТРОЛЬНАЯ РАБОТА №1 В задачах 1-20 решить заданную систему уравнений, пользуясь формулами Крамера. Сделать проверку полученного решения.
Решение типового примера. Пусть требуется, используя формулы Крамера, решить систему
Подсчитаем сначала главный определитель системы
У нас
Так как
Осуществим проверку правильности полученного решения, подставив его в каждое уравнение заданной системы:
0-2·(-1)+2=4, 2·0+(-1)+3·2=5, 3·0+4·(-1)+2=-2. Все три равенства верные, поэтом делаем вывод о правильности полученного ранее решения x=0, y=-1, z=2.
В задачах 21-40 даны координаты вершин треугольника АВС. Найти: 1) длину стороны АВ, 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) внутренний угол В в радианах с точностью до 0,01; 4) уравнение медианы АЕ; 5) уравнение и длину высоты СD; 6) уравнение прямой, проходящей через точку Е параллельно стороне АВ и точку М её пересечения с высотой СD. 21. А(-8; -3), В(4; -12), С(8; 10). 22. А(-5; 7), В(7; -2), С(11; 20). 23. А(-12; -1), В(0; -10), С(4; 12). 24. А(-10; 3), В(2; 0), С(6; 22). 25. А(0; 0), В(3; 4), С(4; 2). 26. А(0; 2), В(12; -7), С(16; 15). 27. А(-9; 6), В(3; -3), С(7; 19). 28. А(3; -3), В(6; 1), С(7; -1). 29. А(1; 0), В(13; -9), С(17; 13). 30. А(4; 0), В(7; 4), С(8; 2). 31. А(-2; 7), В(10; -2), С(8; 12). 32. А(-6; 8), В(6; -1), С(4; 13). 33. А(0; 2), В(3; 6), С(4; 4). 34. А(-10; 5), В(2; -4), С(0; 10). 35. А(-4; 12), В(8; 3), С(6; 17). 36. А(-3; 10), В(9; 1), С(7; 15). 37. А(4; -3), В(7; 1), С(8; -1). 38. А(2; -2), В(5; 2), С(6; 0). 39. А(-1; 1), В(2; 5), С(3; 3). 40. А(-5; 9), В(7; 0), С(5; 14).
Решение типового примера. Пусть А(-1;2), В(5;-1), С(-4;-5). 1. Расстояние d между точками A(x1 ; y1) и B(x2; y2) определяется по формуле d= воспользовавшись которой находим длину стороны АВ:
2. Уравнение прямой, проходящей через две заданные точки плоскости А(x1;y1) и B(x2;y2) имеет вид
Подставляя в (2) координаты точек А и В, получаем уравнение стороны АВ:
Угловой коэффициент У нас Аналогично получим уравнение прямой ВС и найдём её угловой коэффициент:
Далее 3. Для нахождения внутреннего угла нашего треугольника воспользуемся формулой
Отметим, что порядок вычисления разности угловых коэффициентов, стоящие в числителе этой дроби, зависит от взаимного расположения прямых АВ и ВС. Подумайте, как бы Вы стали искать внутренние углы А и С треугольника АВС? Подставив ранее вычисленные значения
Теперь, воспользовавшись таблицами В.М. Брадиса или инженерным микрокалькулятором, получаем 4. Для составления уравнения медианы АЕ найдём сначала координаты точки Е, которая лежит на середине отрезка ВС:
Теперь, подставив в (2) координаты точек А и Е, получаем уравнение медианы:
5. Для составления уравнения высоты CD воспользуемся уравнением прямой, проходящей через заданную точку
и условием перпендикулярности прямых АВ и СD, которое выражается соотношением
Для вычисления длины высоты CD воспользуемся формулой отыскания расстояния d от заданной точки
Подставив в (5) вместо
6. Так как искомая прямая EF параллельна прямой АВ, то
Для отыскания координат точки М решаем совместно уравнения прямых EF и CD:
Таким образом, Треугольник АВС, высота CD, медиана AE, прямая EF и точка М построены в системе координат xOy на рис. 1.
В задачах 41-60 даны координаты вершин пирамиды ABCD. Требуется: 1) Записать векторы 2) Найти угол между векторами 3) Найти проекцию вектора 4) Найти площадь грани АВС; 5) Найти объём пирамиды ABCD; 6) Составить уравнение ребра АС; 7) Составить уравнение грани АВС. 41. А(2; -3; 1), В(6; 1; -1), С(4; 8; -9), D(2; -1; 2). 42. А(5; -1; -4), В(9; 3; -6), С(7; 10; -4), D(5; 1; -3). 43. А(1; -4; 0), В(5; 0; -2), С(3; 7; -10), D(1; -2; 1). 44. А(-3; -6; 2), В(1; -2; 0), С(-1; 5; -8), D(-3; -4; 3). 45. А(-1; 1; -5), В(3; 5; -7), С(1; 12; -15), D(-1; 3; -4). 46. А(-4; 2; -1), В(0; 6; -3), С(-2; 13; -11), D(-4; 4; 0). 47. А(0; 4; 3), В(4; 8; 1), С(2; 15; -7), D(0; 6; 4). 48. А(-2; 0; -2), В(2; 4; -4), С(0; 11; -12), D(-2; 2; -1). 49. А(3; 3; -3), В(7; 7; -5), С(5; 14; -13), D(3; 5; -2). 50. А(4; -2; 5), В(8; 2; 3), С(6; 9; -5), D(4; 0; 6). 51. А(-5; 0; 1), В(-4; -2; 3), С(6; 2; 11), D(3; 4; -9). 52. А(1; -4; 0), В(2; -6; 2), С(12; -2; 10), D(9; 0; 8). 53. А(-1; -2; -8), В(0; -4; -6), С(10; 0; 2), D(7; 2; 0). 54. А(0; 2; -10), В(1; 0; -8), С(11; 4; 0), D(8; 6; -2). 55. А(3; 1; -2), В(4; -1; 0), С(14; 3; 8), D(11; 5; 6). 56. А(-8; 3; -1), В(-7; 1; 1), С(3; 5; 9), D(0; 7; 7). 57. А(2; -1; -4), В(3; -3; -2), С(13; 1; 6), D(10; 3; 4). 58. А(-4; 5; -5), В(-3; 3; -3), С(7; 7; 5), D(4; 9; 3). 59. А(-2; -3; 2), В(-1; -5; 4), С(9; -1; 12), D(6; 1; 10). 60. А(-3; 4; -3), В(-2; 2; -1), С(8; 6; 7), D(5; 8; 5).. Решение типового примера. Пусть А(0; 0; 1), В(2; 3; 5), С(6; 2; 3), D(3; 7; 2). 1. Известно, что произвольный вектор
где
Если заданы точки
то есть
Воспользовавшись формулой (2) и координатами заданных точек A, B, C, D, получим:
Если вектор
Используя формулу (3), получаем модули найденных векторов:
Известна формула
где
У нас
то есть 3. Известно, что
то есть в нашем случае
4. Воспользуемся формулой нахождения площади треугольника, построенного на векторах
где
В нашем примере
Таким образом,
Объём пирамиды, построенной на трёх некомпланарных векторах
где
У нас
то есть 6. Известно, что уравнение прямой, проходящей через две заданные точки пространства
Подставив в (4) координаты точек А и С, получим
то есть уравнение ребра АС окончательно запишется следующим образом:
7. Уравнение плоскости, проходящее через три заданные точки
Подставляя в него координаты точек А, В, С, получим
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 487; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.19.210 (0.011 с.) |

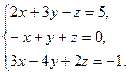
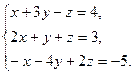
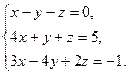
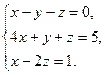
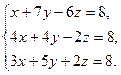
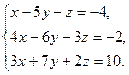



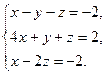
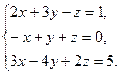
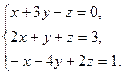



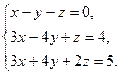
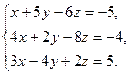
 , воспользовавшись следующим правилом вычисления определителей третьего порядка:
, воспользовавшись следующим правилом вычисления определителей третьего порядка: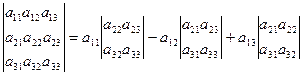 .
.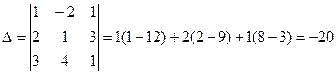 .
.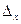 ,
,  ,
, 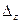 .
.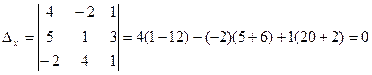 ,
, ,
,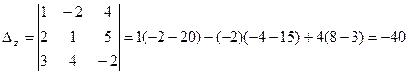 .
. Далее, воспользовавшись формулами Крамера, окончательно получим
Далее, воспользовавшись формулами Крамера, окончательно получим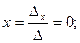
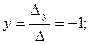
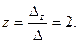
 (1)
(1)
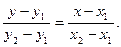 (2)
(2)
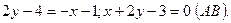
 прямой АВ найдём, преобразовав полученное уравнение к виду уравнения прямой с угловым коэффициентом
прямой АВ найдём, преобразовав полученное уравнение к виду уравнения прямой с угловым коэффициентом 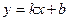 .
.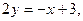 то есть
то есть 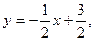 откуда
откуда 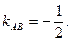

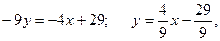 т.е.
т.е. 
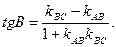 (3)
(3)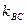 в (3), находим:
в (3), находим: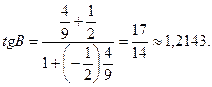
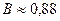 рад.
рад.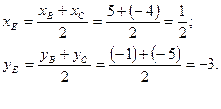
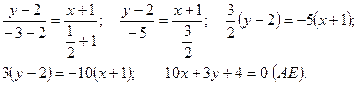
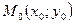 с заданным угловым коэффициентом
с заданным угловым коэффициентом  , которое имеет вид
, которое имеет вид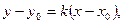 (4)
(4)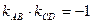 , откуда
, откуда  Подставив в (4) вместо
Подставив в (4) вместо 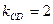 , а вместо
, а вместо 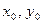 координаты точки С, получим уравнение высоты CD:
координаты точки С, получим уравнение высоты CD: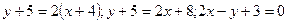 (CD).
(CD). до заданной прямой с уравнением
до заданной прямой с уравнением  , которая имеет вид
, которая имеет вид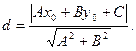 (5)
(5)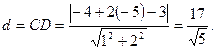
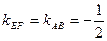 . Подставив в уравнение (4) вместо x0, y0 координаты точки Е, а вместо
. Подставив в уравнение (4) вместо x0, y0 координаты точки Е, а вместо  , получаем уравнение прямой EF:
, получаем уравнение прямой EF:
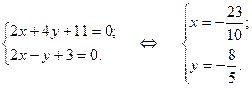
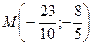 .
.
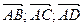 в системе орт
в системе орт 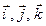 и найти модули этих векторов;
и найти модули этих векторов; ;
; на вектор
на вектор  ;
;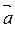 представляется в системе орт
представляется в системе орт 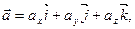 (1)
(1) координаты вектора
координаты вектора 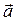 в системе координат, порождённой ортами, причём
в системе координат, порождённой ортами, причём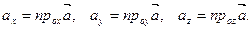
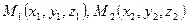 , то для вектора
, то для вектора 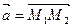
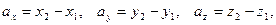
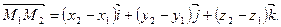 (2)
(2)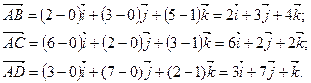
 задан формулой (1),то его модуль вычисляется следующим образом:
задан формулой (1),то его модуль вычисляется следующим образом: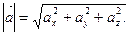 (3)
(3)
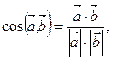
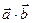 скалярное произведение векторов
скалярное произведение векторов  , которое можно вычислить следующим образом:
, которое можно вычислить следующим образом:

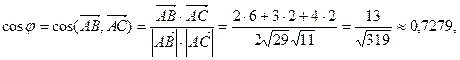
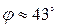 .
.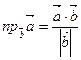 ,
,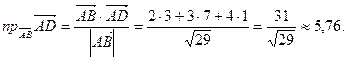
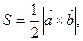
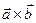 векторное произведение векторов, которое можно вычислить по следующему правилу:
векторное произведение векторов, которое можно вычислить по следующему правилу: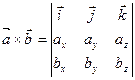 .
.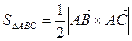 , причём
, причём
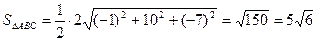 (кв. ед.).
(кв. ед.).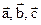 можно найти по формуле
можно найти по формуле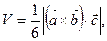
 смешанное произведение векторов, которое вычисляется следующим образом:
смешанное произведение векторов, которое вычисляется следующим образом: .
.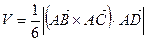 , где
, где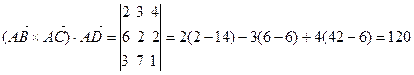 ,
, (куб.ед.).
(куб.ед.).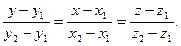
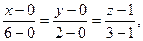
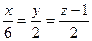 или
или  .
.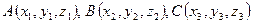 можно записать в виде
можно записать в виде