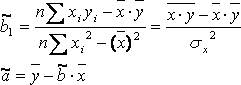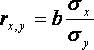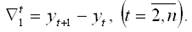Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод наименьших квадратов для моделей регрессии, нелинейных по факторным переменнымСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Метод наименьших квадратов для моделей регрессии, нелинейных по факторным переменным Если модель регрессии является нелинейной по факторным переменным или нелинейной по оцениваемым коэффициентам, но внутренне линейной, то неизвестные коэффициенты данных моделей можно оценить с помощью классического метода наименьших квадратов. Рассмотрим применение метода наименьших квадратов для определения неизвестных параметров модели регрессии, нелинейной по факторным переменным.
Параболическая функция второго порядка вида
является моделью регрессии, нелинейной по факторным переменным xi. Метод наименьших квадратов позволяет получить такие оценки параметров β0,β1 и β2 при которых сумма квадратов отклонений фактических значений результативного признака ỹ от расчетных (теоретических) β минимальна:
В процессе минимизации исходной функции регрессии неизвестными являются только значения коэффициентов β0,β1 и β2, потому что значения результативной и факторной переменных известны из наблюдений. Для определения минимума функции трёх переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений. Составим стационарную систему уравнений для функционала F, не пользуясь методом замен:
После элементарных преобразований стационарной системы уравнений, получим систему нормальных уравнений, позволяющую определить значения неизвестных коэффициентов параболической функции:
Данная система является системой нормальных уравнений относительно параметров
для параболической функции второго порядка.
Полученная система нормальных уравнений является квадратной, т. к. количество уравнений равняется количеству неизвестных переменных, поэтому коэффициенты
можно рассчитать с помощью метода Крамера или метода Гаусса.
Если рассматривать полиномиальную функцию n-ой степени вида
то для определения оценок неизвестных коэффициентов данной модели регрессии методом наименьших квадратов минимизируется функционал F:
Для определения минимума функции нескольких переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений:
Решением данной стационарной системы уравнений будут оценки неизвестных коэффициентов полиномиальной функции n-ой степени.
Оценка точности и качества прогнозов К ним относятся такие показатели которые позволяют прогнозне ошибки разложить на составляющие. Особенно такой анализ важен для циклически изменяющихся переменных, когда необходимо прогнозировать нетолько общее развитие прогнозирование но и поворотные точки цикла. Большинство показателей точности прогноза в своей основе содержит среднеквадратическую ошибку. Преобразую данную ошибку можно её разложить на следующие 3 составляющие:
Vs=
Vg=
Vk= т.к. это доля от целого то сумма всегда равна 1 Vs+Vσ+Vk=1 Данные доли показывают несоответтвия по смещению среднеквадратической ошибке и ковариации. Ковариация – это двухмерный аналог дисперсии т.е. совместная вариация или совместное рассеивание сразу 2-х переменных. Проверка точности одного прогноза может мало что дать исследователю т.к. на формировании рассматриваемого явления как правило имеет множество разнообразных факторов. Полное совпадение или значительное расхождение прогнозов может быть следствием особоблагоприятных или неблагоприятных стичений обстоятельств. Поэтому качество прогнозов абсолютные, сравнительные, качественные прогнозы выходит на 1-й план вопросов достоверности этих прогнозов и адекватности этих моделей. Регрессионный анализ Регрессионный(линейный) анализ — статистический метод исследования зависимости между зависимой переменной Y и одной или несколькими независимыми переменными X1,X2,...,Xp. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных, а не причинно-следственные отношения. Цели регрессионного анализа Определение степени детерминированности вариации критериальной (зависимой) переменной предикторами (независимыми переменными) Предсказание значения зависимой переменной с помощью независимой(-ых) Определение вклада отдельных независимых переменных в вариацию зависимой Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа. Показатели вариации Вариацию можно определить как количественное различие значений одного и того же признака у отдельных единиц совокупности. Термин «вариация» имеет латинское происхождение - variatio, что означает различие, изменение, колеблемость. Изучение вариации в статистической практике позволяет установить зависимость между изменением, которое происходит в исследуемом признаке, и теми факторами, которые вызывают данное изменение. Для измерения вариации признака используют как абсолютные, так и относительные показатели. К абсолютным показателям вариации относят: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсию. К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение и др. Размах вариации R. Это самый доступный по простоте расчета абсолютный показатель, который определяется как разность между самым большим и самым малым значениями признака у единиц данной совокупности:
Размах вариации (размах колебаний) - важный показатель колеблемости признака, но он дает возможность увидеть только крайние отклонения, что ограничивает область его применения. Для более точной характеристики вариации признака на основе учета его колеблемости используются другие показатели. Среднее линейное отклонение d, которое вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности. Эта величина определяется как средняя арифметическая из абсолютных значений отклонений от средней. Так как сумма отклонений значений признака от средней величины равна нулю, то все отклонения берутся по модулю.
Формула среднего линейного отклонения (простая)
Формула среднего линейного отклонения (взвешенная)
При использовании показателя среднего линейного отклонения возникают определенные неудобства, связанные с тем, что приходится иметь дело не только с положительными, но и с отрицательными величинами, что побудило искать другие способы оценки вариации, чтобы иметь дело только с положительными величинами. Таким способом стало возведение всех отклонений во вторую степень. Обобщающие показатели, найденные с использованием вторых степеней отклонений, получили очень широкое распространение. К таким показателям относятся среднее квадратическое отклонение и среднее квадратическое отклонение в квадрате, которое называют дисперсией. Средняя квадратическая простая
Средняя квадратическая взвешенная
Дисперсия есть не что иное, как средний квадрат отклонений индивидуальных значений признака от его средней величины. Формулы дисперсии взвешенной и простой:
Расчет дисперсии можно упростить. Для этого используется способ отсчета от условного нуля (способ моментов), если имеют место равные интервалы в вариационном ряду. Кроме показателей вариации, выраженных в абсолютных величинах, в статистическом исследовании используются показатели вариации (V), выраженные в относительных величинах, особенно для целей сравнения колеблемости различных признаков одной и той же совокупности или для сравнения колеблемости одного и того же признака в нескольких совокупностях. Данные показатели рассчитываются как отношение размаха вариации к средней величине признака (коэффициент осцилляции), отношение среднего линейного отклонения к средней величине признака (линейный коэффициент вариации), отношение среднего квадратического отклонения к средней величине признака (коэффициент вариации) и, как правило, выражаются в процентах. Формулы расчета относительных показателей вариации:
где VR - коэффициент осцилляции; - линейный коэффициент вариации; - коэффициент вариации. Из приведенных формул видно, что чем больше коэффициент V приближен к нулю, тем меньше вариация значений признака. В статистической практике наиболее часто применяется коэффициент вариации. Он используется не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному).
Критерий Дарбина — Уотсона Критерий Дарбина — Уотсона (или DW-критерий) — статистический критерий, используемый для нахождения автокорреляции первого порядка элементов исследуемой последовательности. Наиболее часто применяется при анализе временных рядов и остатков регрессионных моделей. Критерий назван в честь Джеймса Дарбина и Джеффри Уотсона. Критерий Дарбина — Уотсона рассчитывается по следующей формуле
где ρ1 — коэффициент автокорреляции первого порядка. В случае отсутствия автокорреляции d = 2, при положительной автокорреляции d стремится к нулю, а при отрицательной — к 4:
На практике применение критерия Дарбина — Уотсона основано на сравнении величины d с теоретическими значениями dL и dU для заданных числа наблюдений n, числа независимых переменных модели k и уровня значимости α. Если d < dL, то гипотеза о независимости случайных отклонений отвергается (следовательно присутствует положительная автокорреляция); Если d > dU, то гипотеза не отвергается; Если dL < d < dU, то нет достаточных оснований для принятия решений. Когда расчетное значение d превышает 2, то с dL и dU сравнивается не сам коэффициент d, а выражение (4 − d). Также с помощью данного критерия выявляют наличие коинтеграции между двумя временными рядами. В этом случае проверяют гипотезу о том, что фактическое значение критерия равно нулю. С помощью метода Монте-Карло были получены критические значения для заданных уровней значимости. В случае, если фактическое значение критерия Дарбина — Уотсона превышает критическое, то нулевую гипотезу об отсутствии коинтеграции отвергают. Недостатки: Неприменим к моделям авторегрессии. Не способен выявлять автокорреляцию второго и более высоких порядков. Даёт достоверные результаты только для больших выборок.
Устранение автокорреляции. Для устравнения влияния предыдущего уровня на последующий можно из каждого последующего уровня вычесть предыдущий, т.е. получить первые разности и изучить связь между ними. Этот метод называется метод первых разностей. Сравнивается коэффициент корреляции по исходному ряду. R=∑∆y∆y/ √∑∆x2∆y2 Обычно при устранении автокорреляции сама связь выявляется значительно ниже чем до приобразования ряда. Ранее мы рассматривали что большинство экономических явлений в случае определения теоретического уровнения регрессии будет иметь не линейный характер. Если связь между результативным и факторным признаками не линейная и нами была выявлена автокорреляция то её устраняют методом 1-х разностей. Коэффициент эластичности. Эласти́чность (англ. elasticity) — численная характеристика изменения одного показателя (например:спроса или предложения) к другому показателю (например: цене, доходу) и показывающая, на сколько процентов изменится первый показатель при изменении второго на 1%. Товары с эластичным спросом по цене: Предметы роскоши (драгоценности, деликатесы) Товары, стоимость которых ощутима для семейного бюджета (мебель, бытовая техника) Легкозаменяемые товары (мясо, фрукты) Товары с неэластичным спросом по цене: Предметы первой необходимости (лекарства, обувь, электричество) Товары, стоимость которых незначительна для семейного бюджета (карандаши, зубные щётки) Труднозаменяемые товары (хлеб, электрические лампочки, бензин) Эластичными (по цене) считаются спрос или предложение, когда изменение величины спроса (предложения) больше изменения цены (|E|>1). Неэластичными считаются спрос или предложение, когда изменение величины спроса (предложения) меньше изменения цены (|E|<1). Эластичность спроса относительно цены Эластичность спроса по цене, ценовая эластичность спроса (price elasticity of demand) — относительное изменение объема спроса при изменении цены на 1 %.
Для измерения процентного изменения величины спроса используется формула средней точки Аллена.
Встречается так же упрощённый расчёт:
Различают точечную и дуговую эластичность. Точечная эластичность — эластичность, измеренная в одной точке кривой спроса или предложения; Точечная эластичность может быть определена, если провести касательную кривой спроса. Значение точечной эластичности обратно пропорционально тангенсу угла наклона касательной. Дуговая эластичность — это показатель средней реакции спроса на изменение цены выраженной кривой спроса на некотором отрезке D1D2. На эластичность влияют сроки хранения и особенности производства. В зависимости от значения коэффициента Ed различают: совершенную неэластичность (коэффициент Ed = 0). К товарам с совершенно неэластичным спросом по цене относятся товары, без которых невозможно обойтись, например, соль, инсулин для диабетиков. неэластичный спрос (коэффициент |Ed| < 1); спрос, имеющий единичную эластичность (коэффициент |Ed| = 1). эластичный спрос (коэффициент |Ed| > 1); совершенно эластичный спрос (коэффициент |Ed| = бесконечности) Данный вид эластичности характерен для товаров в условиях совершенного рынка, где никто не может повлиять на его цену, следовательно, она остается неизменной. Для подавляющего большинства товаров зависимость между ценой и спросом обратная, то есть коэффициент получается отрицательным. Минус обычно принято опускать и оценка производится по модулю. Тем не менее, встречаются случаи, когда коэффициент эластичности спроса оказывается положительным — например, это характерно для товаров Гиффена. Факторы, влияющие на эластичность: Наличие заменителей. Чем больше товаров-субститутов, тем эластичнее спрос на данный товар. Удельный вес товара в бюджете потребителя. Чем больше удельный вес, тем выше ценовая эластичность спроса. Размер дохода. Качество товара. Если товар — предмет роскоши, спрос эластичен; если товар первой необходимости, спрос неэластичен. Размеры запаса. Чем больше запас, тем эластичней спрос. Ожидания потребителя. Парный регрессионный анализ
Одним из методов изучения стохастических связей между признаками является регрессионный анализ. Регрессионный анализ представляет собой вывод уравнения регрессии, с помощью которого находится средняя величина случайной переменной (признака-результата), если величина другой (или других) переменных (признаков-факторов) известна. Он включает следующие этапы: выбор формы связи (вида аналитического уравнения регрессии); оценку параметров уравнения; оценку качества аналитического уравнения регрессии.
Наиболее часто для описания статистической связи признаков используется линейная форма. Внимание к линейной связи объясняется четкой экономической интерпретацией ее параметров, ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связи для выполнения расчетов преобразуют (путем логарифмирования или замены переменных) в линейную форму. В случае линейной парной связи уравнение регрессии примет вид: Параметры данного уравнения а и b оцениваются по данным статистического наблюдения x и y. Результатом такой оценки является уравнение: Наиболее часто для оценки параметров используют метод наименьших квадратов (МНК). Метод наименьших квадратов дает наилучшие (состоятельные, эффективные и несмещенные) оценки параметров уравнения регрессии. Но только в том случае, если выполняются определенные предпосылки относительно случайного члена (u) и независимой переменной (x). Задача оценивания параметров линейного парного уравнения методом наименьших квадратов состоит в следующем: получить такие оценки параметров Формально критерий МНК можно записать так:
Проиллюстрируем суть данного метода графически. Для этого построим точечный график по данным наблюдений (xi,yi, i=1;n) в прямоугольной системе координат (такой точечный график называют корреляционным полем). Попытаемся подобрать прямую линию, которая ближе всего расположена к точкам корреляционного поля. Согласно методу наименьших квадратов линия выбирается так, чтобы сумма квадратов расстояний по вертикали между точками корреляционного поля и этой линией была бы минимальной.
Математическая запись данной задачи:
Значения yi и xi i=1; n нам известны, это данные наблюдений. В функции S они представляют собой константы. Переменными в данной функции являются искомые оценки параметров -
В результате получим систему из 2-ух нормальных линейных уравнений:
Решая данную систему, найдем искомые оценки параметров:
Правильность расчета параметров уравнения регрессии может быть проверена сравнением сумм (возможно некоторое расхождение из-за округления расчетов). Знак коэффициента регрессии b указывает направление связи (если b>0, связь прямая, если b <0, то связь обратная). Величина b показывает на сколько единиц изменится в среднем признак-результат -y при изменении признака-фактора - х на 1 единицу своего измерения. Формально значение параметра а – среднее значение y при х равном нулю. Если признак-фактор не имеет и не может иметь нулевого значения, то вышеуказанная трактовка параметра а не имеет смысла. Оценка тесноты связи между признаками осуществляется с помощью коэффициента линейной парной корреляции - rx,y. Он может быть рассчитан по формуле:
Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b:
Область допустимых значений линейного коэффициента парной корреляции от –1 до +1. Знак коэффициента корреляции указывает направление связи. Если rx, y>0, то связь прямая; если rx, y<0, то связь обратная. Если данный коэффициент по модулю близок к единице, то связь между признаками может быть интерпретирована как довольно тесная линейная. Если его модуль равен единице ê rx, y ê =1, то связь между признаками функциональная линейная. Если признаки х и y линейно независимы, то rx,y близок к 0. Для оценки качества полученного уравнения регрессии рассчитывают теоретический коэффициент детерминации – R2yx:
где d 2 – объясненная уравнением регрессии дисперсия y; e 2- остаточная (необъясненная уравнением регрессии) дисперсия y; s 2 y - общая (полная) дисперсия y. Коэффициент детерминации характеризует долю вариации (дисперсии) результативного признака y, объясняемую регрессией (а, следовательно, и фактором х), в общей вариации (дисперсии) y. Коэффициент детерминации R2yx принимает значения от 0 до 1. Соответственно величина 1-R2yx характеризует долю дисперсии y, вызванную влиянием прочих неучтенных в модели факторов и ошибками спецификации. При парной линейной регрессии R 2yx=r2 yx.
Производственные функции Производственной функцией называется экономико-математическая модель, с помощью которой можно охарактеризовать зависимость результатов производственной деятельности предприятия, отрасли или национальной экономики в целом от повлиявших на эти результаты факторов. Факторами производственной функции могут являться следующие переменные: 1) объём выпущенной продукции (в стоимостном или натуральном выражении); 2) объём основного капитала или основных фондов; 3) объём трудовых ресурсов или трудовых затрат (измеряемое количеством рабочих или количеством человеко-дней); 4) затраты электроэнергии; 5) количество станков, потребляемое в производстве и др. Однофакторные производственные функции (т. е. функции с одной факторной переменной) относятся к наиболее простым производственным функциям. В данном случае результативной переменной является объём производства у, который зависит от единственной факторной переменной х. В качестве факторной переменной может выступать любая из вышеназванных переменных. Основными разновидностями однофакторных производственных функций являются: 1) линейная однофакторная производственная функция вида: y=β0+β1x, например, производственная функция зависимости объёма производимой продукции от величины затрат определённого ресурса. Линейная однофакторная производственная функция характеризуется двумя особенностями: а) если величина факторной переменной х равна нулю, то объём производства у не будет нулевым, потому что y=β0(β0›0); б) объём произведённой продукции у неограниченно возрастает при увеличении затрат определённого фактора х на постоянную величину β1 (β1›0). Однако данное свойство линейной однофакторной производственной функции чаще всего справедливо только на практике; 2) параболическая однофакторная производственная функция вида:
при условиях β0›0, β1›0, β2›0. Данная функция характеризуется тем, что при росте затрат ресурса х, объём произведённой продукции у вначале возрастает до некоторой максимальной величины, а затем снижается до нуля; 3) степенная однофакторная производственная функция вида:
при условиях β0›0, β1›0. Данная функция характеризуется тем, что с ростом затрат ресурса х, объём производства у возрастает без ограничений; 4) показательная однофакторная производственная функция вида:
при условиях 0‹β1‹0. Данная функция характеризуется тем, что с ростом затрат ресурса х объём произведённой продукции у также растёт, стремясь при этом к значению параметра β0. 5) гиперболическая однофакторная производственная функция вида:
Данная функция практически не применяется при изучении зависимости объёма производства от затрат какого-либо ресурса, потому что нет необходимости в изучении ресурсов, увеличение которых приводит к уменьшению объёма производства. Двухфакторные производственные функции (функции с двумя факторными переменными) характеризуют зависимость объёма производства от каких-либо двух факторов, чаще от факторов объёма основного капитала и трудовых ресурсов. Чаще всего используются такие двухфакторные производственные функции как функции Кобба-Дугласа и Солоу. Для наглядного изображения двухфакторных производственных функций строят графики семейства кривых, основанных на различном сочетании двух факторов, но дающих в результате одно и то же значение объёма выпуска продукции. Кривые, построенные на основании равенства f(x1,x2)=const, называются изоквантами. Изоквантой называется сочетание минимально необходимых ресурсных затрат для заданного уровня объёма производства. Многофакторные производственные функции используются для изучения зависимости объёма производства от n-го количества факторов производства. Общий вид многофакторной производственной функции: y=f(xi), где
Аналитический вид тренда
Метод аналитического выравнивания с помощью функций времени или кривых роста является основным методом представления тренда в аналитическом виде, используемым в эконометрике. Суть данного метода заключается в аппроксимации временного ряда определённой формой регрессионной кривой. При этом наиболее проблематичным является вопрос о выборе функции тренда. Выбор выравнивающей кривой может осуществляться на основании заранее заданных критериев, к которым относятся: 1) множественный коэффициент детерминации; 2) сумма квадратов отклонений наблюдаемых значений временного ряда от теоретических значений (рассчитанных с помощью функции тренда). Методом конечных разностей называется метод, позволяющий подобрать подходящую форму кривой. Его применение возможно в том случае, если временной ряд содержит равностоящие друг от друга уровни. Конечной разностью первого порядка (разностным оператором первого порядка) называется разность между соседними уровнями временного ряда:
Разностным оператором второго порядка (конечной разностью второго порядка) называется разность между соседними разностными операторами первого порядка:
В общем случае разностным оператором i-го порядка называется разность между соседними разностными операторами (i-1)-го порядка:
Если разностные операторы первого порядка постоянны и равны между собой
а разностные операторы второго порядка равны нулю
то тренд изучаемого временного ряда можно аппроксимировать линейной функцией вида y=a+β*t+ε. Если разностные операторы второго порядка постоянны и равны между собой
а разностные операторы третьего порядка равны нулю
то тренд изучаемого временного ряда можно аппроксимировать параболической функцией второго порядка вида y=a+β1*t+β2*t2.. Следовательно, порядок разностных операторов, являющихся постоянными для данного временного ряда, определяет степень уравнения тренда: y=∑βj*tj. Оценки неизвестных коэффициентов уравнения тренда рассчитываются с помощью классического метода наименьших квадратов. Если тренд временного ряда можно аппроксимировать линейной функцией, то её коэффициенты можно рассчитать с помощью метода моментов. При этом в модель вводится новая переменная времени T, началом координат которой является середина временного ряда. Таким образом, её сумма по всем элементам равняется нулю. Для временного ряда, количество уровней которого является нечётным, переменная T=0 соответствует середине данного ряда. Выше нулевого уровня проставляются числа -1, -2, -3,…., а ниже данного уровня – числа +1, +2, +3,… Для временного ряда, количество уровней которого является чётным, числа -1, -2, -3 и т. д. проставляются до середины ряда, а числа +1, +2, +3 – ставятся после середины ряда. Линейная модель регрессии с учётом новой переменной принимает вид: yt=a+β*Tt+εt. Оценки неизвестных коэффициентов данной модели рассчитываются из системы нормальных уравнений:
Решением данной системы будут оценки коэффициентов уравнения тренда:
Метод экстрополяции В случае когда необходимо определить какие либо элементы за пределами данного ряда может быть использована экстрополяция. Экстрополяция - это метод определения количественных характеристик для савокупностей и явлений для которых нет данных. Определяются эти недостающие данные путём распространения на них результатов полученных из наблюдений над аналогичными савокупностями. Экстрополяция бывает 2-х типов: 1) перспективная 2) ретроспективная 1) Перспективная- это прогнащирование т.е. распространение (экстрополирование) выявленной тенденции имеющегося ряда 2) Ретроспективная – это определение каких то показателей по данному ряду в прошлом. Рассмотрим способы экстрополяции: 1) Экстрополирование по средствам среднего цепного индекса 2) Экстрополирование по средствам среднего темпа изменения
Ky= yi-1- yi/yi
Tср=
Необходимо для определения среднего темпа изменения исследуемого показателя рассматриваются только 1-й и последний элементы ряда, а все колебания внутри ряда ювелируются.
Тср=
Множественная регрессия Изучение связи между тремя и более связанными между собой признаками носит название множественной (многофакторной) регрессии. При исследовании зависимостей методами множественной регрессии требуется определить аналитическое выражение связи между результативным признаков (Y) и множеством факторных признаков (x1, x2, x3,…xn). Построение моделей множественной регрессии включает несколько этапов: · выбор формы связи (уравнения регрессии); отбор факторных признаков; · обеспечение достаточного объема совокупности для получения реальных оценок. Практика построения многофакторных моделей показывает, что все реально существующие зависимости между социально-экономическими явлениями можно описать, используя пять типов моделей: · линейная; · степенная; · показательная; · параболическая; · гиперболическая. Качество уравнения регрессии зависит от степени достоверности и надежности исходных данных и объема совокупности. Немаловажное значение имеет процедура отбора факторов в уравнение. Наиболее приемлемым способом отбора факторных признаков является шаговая регрессия. Сущность метода шаговой регрессии заключается в последовательном включении факторов в уравнение регрессии и последующей проверке их значимости. Если при включении нового фактора в модель, коэффициенты регрессии меняют не только свои значения, но и знаки, а множественный коэффициент корреляции не возрастает, то данный факторный признак признается нецелесообразным для включения в модель связи. Сложность и взаимно переплетение отдельных факторов, обуславливающих исследуемое экономическое явление, могу проявляться в так называемой мультиколлинеарности. Под мультиколлинеарностью понимается тесная зависимость между факторными признаками, включенными в модель. Одним из индикаторов определения мультиколлинеарности между признаками является превышение парным коэффициентом корреляции величины 0,8. При наличии линейной связи между результативным и несколькими факторными признака, а также между парой факторных признаков определяется множественный коэффициент корреляции:
Множественный коэффициент корреляции изменяется в пределах от 0 до 1. Чем ближе R к единице свидетельствует о сильной зависимости между признаками.
Метод интерполяции Это способ определения неизвестных промежуточных значений динамического ряда. Эти неизвестные значения определяются либо на основе известных смежных значений либо на основе установленной взаимосвязи искомого значения с другими значениями. Интерполяция заключается в приближенном отражении внутри определённого отрезка времени.
Коэффициент контингенции Коэффициент ассоциации можно расcчитать по формуле
Нужно иметь в виду, что для одних и тех же данных коэффициент контингенции (изменяется от -1 до +1) всегда меньше коэффициента ассоциации.
Компоненты временного ряда Временным рядом называется ряд наблюдаемых значений изучаемого показателя, расположенных в хронологическом порядке или в порядке возрастания времени. Отдельно взятый временной ряд можно представить как выборочную совокупность из бесконечного ряда значений показателей во времени. Уровнями временного ряда называются наблюдения
из которых состоит данный ряд. Временной ряд называется моментным рядом, если уровень временного ряда фиксирует значение изучаемого показателя на определённый момент времени. Временной ряд называется интервальным рядом, если уровень временного ряда характеризует значение показателя за определённый период времени. Временной ряд называется производным рядом, если уровни ряда представлены в виде производных величин (средних или относительных показателей). Исследование данных, представленных в виде временных рядов, преследует две основные цели: 1) характеристика структуры временного ряда; 2) прогнозирование будущих уровней временного ряда на основании прошлых и настоящих уровней. Достижение поставленных целей возможно с помощью идентификации модели временного ряда. Идентификацией модели временного р
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |

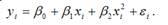
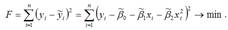
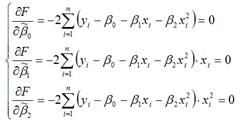
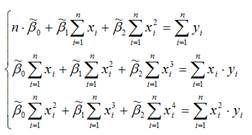
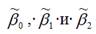
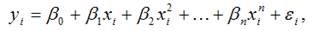
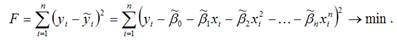
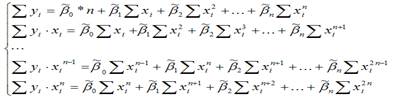






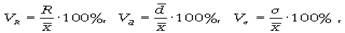


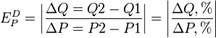 где Q - спрос(количество); P - цена.
где Q - спрос(количество); P - цена.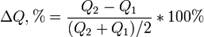
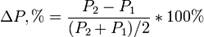
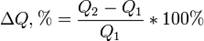
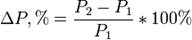
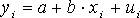
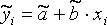 , где
, где  ,
,  - оценки параметров a и b,
- оценки параметров a и b,  - значение результативного признака (переменной), полученное по уравнению регрессии (расчетное значение).
- значение результативного признака (переменной), полученное по уравнению регрессии (расчетное значение). , при которых сумма квадратов отклонений фактических значений результативного признака - yi от расчетных значений –
, при которых сумма квадратов отклонений фактических значений результативного признака - yi от расчетных значений – 


 . Чтобы найти минимум функции 2-ух переменных необходимо вычислить частные производные данной функции по каждому из параметров и приравнять их нулю, т.е.
. Чтобы найти минимум функции 2-ух переменных необходимо вычислить частные производные данной функции по каждому из параметров и приравнять их нулю, т.е.