Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оцінювання параметрів моделі методом найменших квадратів.Содержание книги
Поиск на нашем сайте
Основная идея метода наименьших квадратов, заключается в том, чтобы оценить параметры регрессии, так, чтобы сумма квадратов отклонений фактических значений результативного фактора от рассчитанных, при тех самых значениях независимой переменной Х была минимальной. Необходимо учитывать именно квадратичное отклонение, поскольку сами остатки могут быть как положительными, так и отрицательными и при нахождении суммы они могут аккумулироваться, тем самым давая ошибочные результаты. Таким образом на основе метода наименьших квадратов, можно построить наиболее эффективную линию регрессии, которая качественно будет описывать эконометрическую модель, и которую в последствии можно использовать для нахождения прогнозных значений.
Поняття моделі та етапи її побудови. Эконометрическая модель – это функция или система функций, которая описывает зависимость между социально-экономическими показателями. В общем виде модель можно представить так Y=f(X,u), где Y – зависимая, исследуемая переменная, X – фактор, который влияет на переменную Y, u – случайная составляющая, содержащая влияние сторонних, неучтенных факторов в модели. Для того чтобы построить эконометрическую модель существуют несколько этапов: 1) выдвигание гипотез, четкая постановка задачи; 2) спецификация модели. Включает качественный подбор функции, которая наиболее правильно будет описывать взаимосвязь между переменными; 3) формирования массива исходной информации; 4) оценка параметров модели с помощью МНК; 5) если некоторые предусловия использования МНК не выполняются, следует пересмотреть спецификацию модели; 6) верификация модели в целом, а также оцененных параметров; 7) построение прогноза на основе модели.
Специфікація моделі. Спецификация модели – это аналитическая форма эконометрической модели, на основе исследуемых факторов. Она состоит из функции или системы функций, которые используются для построения моделей и имеет свои особенности. От того насколько правильно будет произведена спецификация модели зависит качество оцененных параметров, а также всей модели в целом, что является особенно важным при построении прогноза или же анализа экономических явлений и процессов. Существуют линейный и нелинейные (степенная, показательная, экспонентная, логарифмическая и др.) модели, имеющие свои особенности. Так, например, при исследовании зависимости объема выпуска продукции от затрат ресурсов, объективней всего применить степенную функцию Кобба-Дугласа.
Передумови застосування методу найменших квадратів. Существуют 4 предусловия использования МНК: 1) математическое ожидание остатков равно нулю; 2) все независимые факторы не коррелируют между случайной величиной; 3) стохастическая составляющая имеют постоянную дисперсию 4) отсутствует взаимосвязь между стохастическими переменными в любых двух наблюдениях; 5) случайная составляющая имеет нормальное распределение; Смысл первого условия заключается в том, что случайное отклонение в среднем не влияет на зависимую переменную. Выполнение этого условия обеспечивает выполнения равенства Выполнение второго условия необходимо только когда, независимая переменная является случайной величиной. Третье условие требует, чтобы значение отклонения в одних наблюдениях не имели существенного отличия в других, если это условие выполняется, то такое явление называется гомоскедастичностью, если не выполняется – гетероскедастичностью. При гетероскедастичности оценки параметров регрессии теряют свою эффективность, то есть они не будут иметь наименьшую дисперсию по сравнению с другими оценками.
Оператор оцінювання МНК. Уравнение регрессии
Введем величину отклонения
Поскольку величина Запишем условие экстремума
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 329; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.9.183 (0.006 с.) |

 ;
;
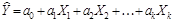 , где
, где  оценки параметров. Это уравнение также можно записать в матричном виде
оценки параметров. Это уравнение также можно записать в матричном виде 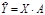 , где
, где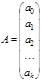


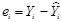 и запишем функцию критерия МНК
и запишем функцию критерия МНК 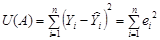 В матричном виде
В матричном виде 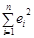 =
= 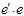 , тогда
, тогда 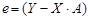

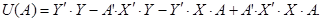
 скаляр, она не меняется в процессе транспонирования, то есть
скаляр, она не меняется в процессе транспонирования, то есть 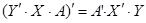 и полученное выражение можно переписать как
и полученное выражение можно переписать как 
 Из этого условия получим систему нормальных уравнений для нахождения параметров регрессии
Из этого условия получим систему нормальных уравнений для нахождения параметров регрессии 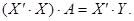 Применяя метод обратной матрицы решение этой системы можем записать так
Применяя метод обратной матрицы решение этой системы можем записать так