
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перевірка наявності автокореляції, тест Дарбіна – Уотсона.Содержание книги
Поиск на нашем сайте
Для проверки наличия автокорреляции остатков чаще всего используют критерий Дарбина-Уотсона(DW) Фактические значения критерия сравниваются с критическими(табличными) для разного количества наблюдений и количества независимых переменных с выбранным уровнем значимости. Фактические значения имеют нижнюю границу DW 1 и верхнюю - DW 2 Когда DW факт < DW 1 остатки имеют автокорреляцию, если Dw факт > DW 2 принимается гипотеза про отсутствие автокорреляции. В случае же DW1 <DW< DW2 конкретные выводы сделать сложно и нужно дальше проводить исследования, увеличиваю совокупность наблюдений. Если остатки являются случайными величинами и имеют нормальное распределение, а не автокоррелированные, то значение DW будет около 2. Если DW<2 автокорреляция положительная, DW>2 то отрицательная. Поскольку критическое значение DW табулированные для положительной величины, то чтобы сделать выводы относительно отрицательной автокорреляции, необходимо отнять рассчитанное значение DW от 4 и эту разницу сравнить со значением критерия DW. Этот критерий предназначен для малых выборок совокупностей.
Критерій фон Неймана. Для выявления автокорреляции можно использовать критерий фон Неймана:
Отсюда
Коефіцієнти автокореляції та їх застосування. Существует нецикличный и цикличных коэффициенты автокорреляции. Нецикличный коэффициент показывает степень взаимосвязи остатков следующего значения с предыдущем. Он находится по формуле:
r может принимать значения в интервале Цикличный коэффициент автокорреляции:
Фактические значения этого критерия сравниваются с табличным для выбранного уровня доверия и совокупности наблюдений. Если r 0факт ³ r 0табл, то существует автокорреляция. Предполагая, что
Оцінювання параметрів моделі з автокорельованими залишками. Существует четыре метода оценивания параметров эконометрической модели с автокоррелированными остатками: 1) метод Эйткена 2) преобразование исходной информации 3) метод Кохрейна-Оркатта 4) метод Дарбина Алгоритм выполнения метода Эйткена: Оператор оценивания этого метода запишется так Поскольку в матрице
На практике для расчета r используется соотношение
Метод преобразования исходной информации Он состоит из двух шагов: 1) преобразование исходной информации при использовании для него параметра r 2) применение метода 1МНК для оценки параметров модели на основе преобразованных данных. Преобразование исходной информации выполняется с помощью матрицы
То есть вместо матрицы Х используется Метод Кохрейна-Оркатта является итеративным методом приближенного поиска параметров Когда модель имеет вид:
Сумма квадратов остатков запишется так:
Алгоритм: 1) Произвольно выбирается значение 2) На основе 1МНК находят параметры 3) Принимая 4) Подставляя Процедура продолжается до тех пор, пока последовательные значения параметров не будут отличатся меньше чем на заданную величину.
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 402; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.216.202 (0.009 с.) |

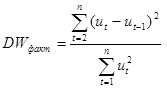 который может принимать значения из промежутка [0, 4]
который может принимать значения из промежутка [0, 4]
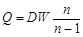 . При
. При 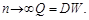 Фактическое значение критерия фон Неймана сравнивается с табличным для выбранного уровня значимости и заданному количестве наблюдений. Если
Фактическое значение критерия фон Неймана сравнивается с табличным для выбранного уровня значимости и заданному количестве наблюдений. Если  то существует положительная автокорреляция, в противном случае – она отсутствует.
то существует положительная автокорреляция, в противном случае – она отсутствует.
 . Отрицательные значения свидетельствуют про отрицательную автокорреляцию, положительные – про положительную автокорреляцию. Значения, которые находятся в кое-какой критической области около нуля, свидетельствуют про отсутствие автокорреляции.
. Отрицательные значения свидетельствуют про отрицательную автокорреляцию, положительные – про положительную автокорреляцию. Значения, которые находятся в кое-какой критической области около нуля, свидетельствуют про отсутствие автокорреляции.
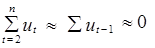 цикличный коэффициент автокорреляции можно записать так
цикличный коэффициент автокорреляции можно записать так 
 , потому что
, потому что 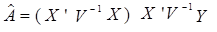 , где
, где  обратная матрица
обратная матрица  ,
,  - обратная матрица
- обратная матрица 
 при
при  приближается до нуля, то матрица, обратная к матрице
приближается до нуля, то матрица, обратная к матрице 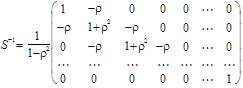
 или
или 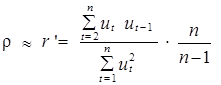
 или
или  :
:
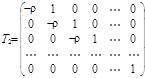
 или
или  , вместо вектора Y -
, вместо вектора Y - 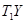 или
или 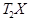
 , которые минимизируют сумму квадратов остатков.
, которые минимизируют сумму квадратов остатков.


 и подставляется в формулу суммы квадратов остатков.
и подставляется в формулу суммы квадратов остатков. и
и 
 и
и 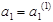 , подставляем в формулу суму квадратов остатков и рассчитаем
, подставляем в формулу суму квадратов остатков и рассчитаем 
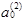 і
і  и т.д.
и т.д.


