
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Измерение концентрации вещества в растворе методом градуировочного графикаСодержание книги
Поиск на нашем сайте
Для измерения концентрации вещества в растворе необходимо предварительно выполнить ряд подготовительных операций в следующей последовательности: выбор длины волны; выбор кюветы; построение градуировочного графика для данного вещества; измерение концентрация вещества.
Выбор длины волны Для достижения наименьшей погрешности в определении концентрации следует правильно выбрать длину волны, на которой будет выполняться измерение. Для этого по спектральной кривой раствора, выбрать такой участок, на котором выполняются следующие условия: - оптическая плотность имеет максимальную величину; - ход кривой примерно параллелен горизонтальной оси т. е. оптическая плотность мало зависит от длины волны. Длина волны, соответствующая этому участку, выбирается для измерения. Если для некоторых растворов второе условие не выполняется, то рабочая длина волны выбирается по первому условию.
Выбор кюветы При определении концентрации вещества в растворе необходимо сделать правильный выбор кюветы. Абсолютная погрешность измерения коэффициента пропускания не превышает 0,5%. Относительная погрешность измерения оптической плотности раствора будет различной и достигает минимума при значении оптической плотности 0,4. Поэтому при работе на фотометре рекомендуется путем соответствующего выбора длины кювет работать вблизи указанного значения оптической плотности, например, в пределах от 0,2 до 0,8. При работе на приборе работайте вблизи указанного значения оптической плотности. Если раствор интенсивно окрашен (темный), пользуйтесь кюветами с малой рабочей длиной (10 мм). В случае слабо окрашенных растворов работайте с кюветами с большей рабочей длиной (50 мм). В предварительно подобранную кювету налейте раствор и измерьте его оптическую плотность, введя в ход лучей соответствующий для данного раствора светофильтр. При измерении ряда растворов кювету заполните раствором средней концентрации. Если полученное значение оптической плотности составляет примерно 0,2—0,8, то данную кювету выбирайте для работы с этим раствором. В том случае, когда это не выполняется, испробуйте кювету другой рабочей длины. Построение градуировочного графика Построение градуировочного графика проводить следующим образом. Приготовить ряд растворов данного вещества с известными концентрациями, охватывающими область возможных изменений концентраций этого вещества в исследуемом растворе.
Измерить оптические плотности всех растворов и построить градуировочный график, откладывая по горизонтальной оси известные концентрации, а по вертикальной — соответствующие им значения оптической плотности, рассчитанные по методу наименьших квадратов. Следует убедиться в том, что зависимость концентрации от оптической плотности — линейная (по критерию Фишера), т. е. выражается на графике прямой линией. По градуировочной кривой (точнее по уравнению линейной регрессии) в дальнейшем определяют неизвестную концентрацию вещества в исследуемых растворах. Для этого раствор наливают в ту же кювету, для которой построена градуировочная кривая, и, включив тот же светофильтр, определяют оптическую плотность раствора. Затем находят концентрацию, соответствующую измеренному значению оптической плотности. Вычисление метрологических характеристик линейного графика Наиболее объективным и правильным является установление математической зависимости А = f (С), которую находят методом регрессионного анализа. В фотометрических методах она выражается обычно линейной и, значительно реже, параболической зависимостью. Вычисление параметров а и b. В общемслучае линейная зависимость выражается уравнением: у = а + bх Значения параметров а и b вычисляют методом регрессионного анализа. Величина a, представляющая собой значение аналитического сигнала при нулевой концентрации определяемого компонента, называется фоновым значением сигнала. Она играет важную роль при оценке чувствительности методик Если имеется п взаимосвязанных пар значений (уi хi),то можно записать:
Здесь n — число измерений; хi, — известное содержание (концентрация) определяемого компонента в i -м стандартном растворе; уi — результат измерении аналитического сигнала (оптической плотности) i- го стандартного раствора. В левой части системы уравнении находятся измеренные значения уi, а в правой — вычисленные значения Yi = а + bхi. Разность между обеими величинами дает погрешность. Аналитически задача метода наименьших квадратов может быть выражена в следующей форме:
SQ = Если yi – (a + bxi) = δi, тогда SQ = Следовательно, задача линейного регрессионного анализа (метода наименьших квадратов) состоит в том, чтобы сумма квадратов отклонений SQ экспериментальных точек (уi хi) вдоль ординаты от проведенной прямой была минимальной. Для того, чтобы найти параметры а и b, удовлетворяющие минимуму SQ, берут частные производные относительно а, затем относительно b, полученные выражения приравнивают нулю и, решая уравнения, находят;
Вычисление метрологических характеристик результатов анализа После того как определена функциональная зависимость у = а + bх и рассчитаны значения а, b, Δа, Δb, по данным измерений аналитического сигнала у (оптическая плотность A) анализируемых проб рассчитывают метрологические характеристики результата анализа. Доверительный интервал результата анализа
|
||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 400; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.175.83 (0.009 с.) |

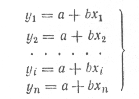
 (yi – Yi)2 =
(yi – Yi)2 = 




