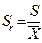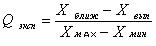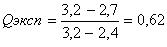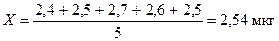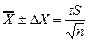Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Погрешности химического анализаСодержание книги
Поиск на нашем сайте
Погрешности фотометрических определений возникают вследствие неправильно проведенной химической реакции, использования грязных кювет, невоспроизводимости установки кювет в фотометрическом приборе и неточной настройкой его на оптический ноль, нестабильности работы источника сплошного излучения и оптической схемы, а также за счет погрешностей при построении градуировочного графика.
По способу вычисления погрешности можно подразделить на абсолютные и относительные. Абсолютной погрешностью называется разность между результатом анализа (
В зависимости от величины
Погрешности классифицируют по характеру причин, их вызывающих, на систематические, случайные и промахи. 1. Систематические погрешности вызваны постоянно действующей причиной, постоянны во всех измерениях и могут быть выявлены и устранены. 2. Случайные погрешности, причины, появления которых неизвестны, но они могут быть оценены методами математической статистики. 3. Промах — это погрешность, резко искажающая результаты анализа. Промах обычно легко обнаруживается и вызвана либо сбоем в работе прибора, либо ошибкой аналитика. Все виды погрешностей хорошо иллюстрируются на рис.2
Рис.2. Систематические и случайные погрешности химического анализа Прямая 1 — систематическая и случайные погрешности отсутствуют, идеализированные результаты анализа равны истинному содержанию вещества в пробе m. Прямая 2 — все измерения не содержат случайных ошибок, но имеют постоянную отрицательную систематическую погрешность Dх. Линия 3 ¾ полностью отсутствует систематическая погрешность. Линия 4 отражает реальную ситуацию, возникающую при измерениях: налицо и систематическая и случайная погрешности. А выпавшая точка символизирует промах.
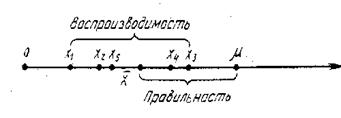
С систематическими и случайными погрешностями связаны понятия воспроизводимости и правильности. Воспроизводимость характеризует степень близости друг к другу единичных определений, рассеяния единичных определений относительно среднего. Правильность характеризует отклонение полученного результата анализа от истинного значения измеряемой величины (рис.3).
Рис.3. Воспроизводимость и правильность химического анализа.
Часто источники систематических и случайных погрешностей одни и те же. Таблица 2 Типы ошибок и частота их возникновения
Основной вклад в общую погрешность вносят методические погрешности, в которые входят - погрешности отбора пробы (60 %), - переведение пробы в удобную для анализа форму (например, сплавление и растворение), - погрешности операции концентрирования и разделения компонентов (30 %); - погрешности, обусловленные природой химической реакции, взятой в основу методики определения компонента; - инструментальные погрешности или погрешности метода измерения составляют 10 %. Случайная ошибка — одиночное значение, не выходящее за пределы установленной для данного исследуемого компонента области, но стремящееся к выходу за эти пределы. Случайные ошибки происходят при всяком измерении, и в том числе при любом аналитическом определении, как бы тщательно оно не проводилось. Наличие их сказывается в том, что при повторном определении того или иного элемента в данном образце, выполненном одним и тем же методом, дают, как правило, не одинаковые, а несколько различающиеся между собой результаты. Они обусловлены: 1. свойствами самой пробы 2. некачественным инструментарием (неточностью пипеток, мерных колб, термоизмерительной аппаратуры, нестабильностью фотометрических приборов) 3. неточностью работы персонала лаборатории (неточное считываение результатов исследования, использование слишком которких шкал и.т.д.) Случайные ошибки практически невозможно исключить совсем, но их можно значительно ограничить после оценки размера ошибки. Чем меньше величина случайных ошибок и меньше разброс индивидуальных показателей, тем лучше воспроизводимость лабораторных исследований. Случайные ошибки могут быть выявлены при постановке анализа в двух или больше параллельных пробах. Для обработки случайных ошибок применяются методы математической статистики. Обычно при проведении химического анализа одного и того же объекта стараются получить от 3 до 7 результатов. Полученный числовой ряд называется выборочной совокупностью. Дисперсия V характеризует рассеяние данных в выборочной совокупности относительно среднего:
Для характеристики рассеяния результатов в выборочной совокупности используют также стандартное отклонение S и относительное стандартное отклонение Sr:
Все три величины — дисперсия, стандартное отклонение и относительное стандартное отклонение характеризуют воспроизводимость результатов химического анализа. Тест, предназначенный для сравнения среднего значения и константы, называется простым тестом Стъюдента. Но прежде чем обрабатывать данные с помощью методов математической статистики нужно исключить из совокупной выборки промахи при помощи Q -критерия (Табл.3). Таблица 3
Делается это следующим образом: рассчитывают Q эксп, равное отношению разности выпадающего результата и величины наиболее близкой к нему, к разности максимальной и минимальной величины результатов определений (размах):
Значения Q -критерия (доверительная вероятность 0,90) Если при заданном числе определений n, Q эксп > Q критерия, известной из табличных данных,то следует этот результат исключить из выборочной совокупности, а если Q эксп < Q критерия, то исключать результат нельзя. Поясним эту операцию примером: при проведении химического анализа были получены следующие результаты: (мкг) 2,4; 3,2; 2,5; 2,7; 2,6; 2,5. Можно ли исключать величину 3,2мкг? Оценим Q эксп:
Находим по таблице Q критерия при 6 параллельных определениях, он в данном случае равен 0,56. Значит, Q эксп > Q критерия, и результат 3,2 мкг следует исключить. Далее из 5 результатов, образующих выборочную совокупность, находим результат анализа — средний результат:
Далее рассчитываем стандартное отклонение S, оно равняется 0,36. Делается это с той целью, чтобы при помощи критерия Стьюдента — t критерия найти доверительный интервал (вероятность) того, что истинная величина будет лежать в пределах, определяемых по следующей формуле:
где t — критерий Стьюдента для заданной вероятности Р. Обычно доверительный интервал рассчитывают для вероятностей, равных 0,90 или 0,95. При n равной 5 величина t для Р = 0,90 и Р = 0,95 t 0,90 = 2,02 и t 0,95 = 2,57. Следовательно, с вероятностью Р = 0,90 истинное значение будет лежать в интервале 2,54 ± 0,32 и с вероятностью 0,95 — 2,54 ± 0,41 мкг. Для оценки достоверности результатов аналитических определений следует учитывать реальные возможности используемого метода или методики. Принято экспериментальные результаты и данные расчеты выражать только достоверно известными цифрами. Например, при гравиметрических методиках взвешивание на обычных аналитических весах позволяет получать результаты с точностью ± 0,2 мг. Если средний результат анализа содержит сотые доли миллиграмма, то это недостоверные цифры. Если эти цифры >> 5, то следует округлять их в сторону ближайшего большего числа, а если меньше 5 — просто не принимать во внимание. Таким образом, результаты гравиметрического анализа 23,67 мг следует округлить до 23,7 мг, а 35,43 до 35,4 мг.
Систематическими ошибками называют погрешности, одинаковые по признаку, происходящие от определенных причин, влияющих на результаты либо в сторону увеличения, либо в сторону уменьшения его. Систематические ошибки можно предусмотреть и устранить или же ввести соответствующие поправки. Наиболее характерными систематическими ошибками являются: - Методические ошибки: Они зависят от особенностей применяемого метода анализа, например, от не вполне количественного протекания реакции, на которой основано определение, от частичной растворимости осадка, от осаждения вместе с ним посторонних примесей, от течения наряду с основной реакцией каких-либо побочных реакций, искажающих результаты титриметрического определения, от свойств примененного при титровании индикатора и т.д. Методические ошибки составляют наиболее серьезную причину искажения результатов количественных определений, устранить их трудно. - Ошибки, зависящие от применяемых приборов и реактивов. Это ошибки, связанные с неравноплечностью или недостаточной точностью весов, с употреблением неповеренных разновесов или сосудов для определения объемов, ошибки, происходящие в результате загрязнения раствора продуктами разрушения стекла, из которого сделана применяемая при анализе посуда. - Ошибки оперативные. Они происходят от неправильного или недостаточно тщательного выполнения аналитических операций: недостаточное промывание осадков, приводящее к постоянному завышению результатов. - Ошибки индивидуальные, зависящие от индивидуальных особенностей аналитиков, например, от его неспособности точно улавливать момент окраски при титровании и т.д. Последние три вида систематических ошибок могут быть учтены и сведены до минимальных величин. Систематические ошибки повторяются при каждом измерении, так как они вызываются постоянными причинами. Поэтому они влияют на всю серию определений. Величина систематической ошибки характеризует правильность результатов анализа. Когда результаты отклоняются от истинного значения на постоянную величину, такая систематическая ошибка называется постоянной ошибкой. Она может вызываться неправильной холостой пробой, а также химической или спектральной интерференцией. Когда ошибки между измеренной и истинной концентрацией пропорциональны концентрации вещества, систематическая ошибка называется пропорциональной ошибкой. Частая причина возникновения пропорциональной ошибки— это ошибочная калибровка. Обнаружение и предупреждение систематических ошибок представляет собой сложную задачу. Систематическую погрешность проще всего выявить с помощью стандартных образцов. Такая проверка одновременно дает возможность испытать и методику, и инструмент измерения аналитического сигнала. Непременное условие применения стандартного образца в химическом анализе — это максимальная близость состава и свойств стандартного образца, и анализируемой пробы. Оценка правильности результатов анализа — проблема значительно более трудная, чем оценка воспроизводимости. Для оценки воспроизводимости нам не надо иметь ничего, кроме серии параллельных результатов измерения. Для оценки же правильности необходимо сравнение результата измерения с истинным значением. Такое значение никогда не может быть известно точно. Важнейшие способы получения информации о действительном значении содержания определяемого компонента в анализируемом образце состоят в следующем. 1. Данные независимого анализа. Образец анализируют повторно, используя другую аналитическую методику, о которой известно (из опыта рактического применения), что она не содержит систематической огрешности. При этом важно, чтобы такая методика была действительно независима от проверяемой, т.е. чтобы она по возможности принадлежала другому методу и не содержала общих операций пробоподготовки. Еще лучше, если такой сравнительный анализ проводят в другой лаборатории, особенно официально аккредитованной. 2. Способ "введено — найдено" (метод добавок). В этом случае аналитик сам готовит для анализа образец с известным содержанием определяемого компонента. Полученный результат ("найдено") сравнивают с заданным содержанием ("введено"). 3. Использование стандартных образцов. В качестве объекта анализа выбирают подходящий СО, а данные о содержании определяемого компонента берут из паспорта СО. Существует ряд специальных приемов, которые позволяют выявить, а во многих случаях и существенно снизить систематическую погрешность. Одним из таких приемов служит способ варьирования размера пробы. В этом случае для анализа используют серию проб различного размера (например, несколько аликвот разного объема) и исследуют зависимость найденного содержания от размера пробы. Предположим, что методика анализа содержит систематическую погрешность А, которая постоянна и не зависит от размера пробы. Погрешность такого типа называется аддитивной. Ее влияние состоит в том, что она увеличивает или уменьшает измеряемое значение аналитического сигнала на одну и ту же постоянную величину. Таким образом, при наличии аддитивной систематической погрешности с увеличением объема аликвоты наблюдается закономерное изменение результата анализа — убывание либо возрастание в зависимости от знака А. Однако не всякая систематическая погрешность является аддитивной. Существуют погрешности другого типа, величина которых прямо пропорциональна размеру пробы (или содержанию определяемого компонента). Такие погрешности называются мультипликативными. Они увеличивают или (чаще) уменьшают значение аналитического сигнала в одно и то же число раз, т.е. изменяют наклон градуировочной зависимости. Очевидно, что такие систематические погрешности описанный способ выявить не может. В то же время мультипликативные систематические погрешности можно значительно уменьшить с помощью специального способа градуировки, называемого способом добавок.
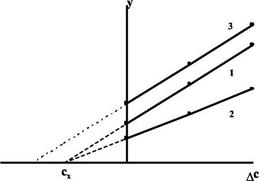
Рис. 4. Градуировка по способу добавок. 1 - систематическая погрешность отсутствует, 2 - наблюдается мультипликативная систематическая погрешность, 3- аддитивная систематическая погрешность
Основная цель способа добавок — беспечение максимально точного соответствия условий градуировки и собственно определения. При использовании способа добавок эти две операции совмещаются воедино: известные содержания определяемого компонента вводят как добавки непосредственно в анализируемый раствор и представляют градуировочную функцию в виде графика зависимости аналитического сигнала от концентрации добавки Ас (рис. 4). Содержание компонента в анализируемом растворе находят путем экстраполяции полученной зависимости на нулевое (или фоновое, если оно известно) значение аналитического сигнала. Легко видеть, что в этом случае даже при наличии мультипликативной погрешности (т.е. изменении тангенса угла наклона градуировочного графика) получается правильный результат (ср. кривые 1 и 2 рис.4). В то же время аддитивную систематическую погрешность способ добавок устранить не может (кривая 3 рис.4).
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 4953; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.95.229 (0.012 с.) |

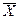 ) и истинным значением (m ) этой величины:
) и истинным значением (m ) этой величины: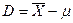
 ´ 100%
´ 100%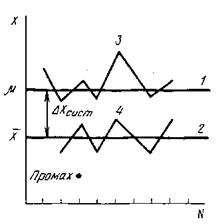

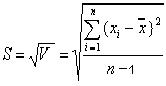 ,
,