
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика измерения параметров трендаСодержание книги
Поиск на нашем сайте
Для определения параметров линейной модели динамического ряда применяют метод наименьших квадратов. Применение метода наименьших квадратов для определения линейной модели динамического ряда подразумевает систему двух линейных уравнений:
Вычислительный процесс нахождения параметров уравнения при сохранении полной идентичности конечных результатов может быть значительно упрощен, если ввести обозначения дат (периодов) времени с помощью натуральных чисел (t), с тем, чтобы
В рядах с нечетным числом членов - это выполняется при условии, что для центрального члена ряда t = 0, вправо t = +1,+2,+3..., а влево: t = -1, -2, -3 ... Если число уровней ряда четное, то два центральных значения принимают вид: вправо t = - 1, а влево t = + 1. Подобрав функцию для описания ряда мы имеем:
a) при нечетном числе уровней: б) при четном числе уровней:
Следовательно, при
Найдя значения а0 и а1 подставляем их в уравнение основной тенденции развития и получаем (при выравнивании ряда динамики по прямой) уравнение прямой линии. Подставляя в полученное уравнение принятые обозначения t, вычислим выравненные по годам уровни ряда динамики.
По окончании расчета основной тенденции целесообразно построить график, на котором следует изобразить исходные данные и теоретические значения уровней ряда. Основная тенденция (тренд) показывает, как воздействуют систематические факторы на уровень ряда динамики, а колеблемость уровней около тренда служит мерой воздействия остаточных (случайных) факторов. Колеблемость уровней около тренда характеризует абсолютный показатель - среднее квадратическое отклонение (σt) и относительный показатель - коэффициент вариации (V):
Аналитическое сглаживание позволяет не только определить общую тенденцию изменения явления на рассматриваемом отрезке времени, но и выполнять расчеты для таких периодов, в отношении которых нет исходных данных, т.е. методом экстраполяции прогнозировать показатели на будущее. Сезонные колебания При анализе рядов динамики важное значение имеет выявление сезонных колебаний (сезонная неравномерность). Сезонными называются периодические колебания, возникающие под влиянием смены времени года. Это сравнительно устойчивые колебания, когда из года в год в одни месяцы уровень явления повышается, а в другие – снижается. Они обусловливаются специфическими условиями, влиянием многочисленных факторов. Наличие сезонных колебаний выявляют аналитически, а также с использованием графического метода, построением линейных диаграмм, на которые наносят данные об объеме явления по месяцам не менее чем за три года. Чтобы исключить влияние различной продолжительности месяцев на уровень сезонных колебаний, целесообразно использовать среднесуточные уровни за каждый месяц. Эти уровни исчисляются путем деления общего объема явления за месяц на число календарных дней в месяце.
Целью изучения сезонных колебаний являются прогнозирование и разработка мер по изменению их во времени.. Большое значение приобретают сезонные колебания в изучении покупательного спроса населения на отдельные товары и виды услуг, а также изменения цен и инфляции и т.д.
При изучении сезонных колебаний необходимо: · выявить общую тенденцию развития явления внутри года; · измерить сезонные колебания изучаемого явления с построением модели сезонной волны.
Измеряются сезонные колебания (сезонная волна) при помощи особых показателей – индексов сезонности (Is). Способы определения индексов сезонности различны в зависимости от характера изменения основной тенденции ряда динамики.
7.4.1. Определение сезонных колебаний для рядов внутригодовой динамики, в которых основная тенденция изменения тренда отсутствует или незначительна, изучение сезонности основано на методе постоянной средней, являющейся средней из всех рассматриваемых уровней. Самый простой способ заключается в том, что для каждого года рассчитывается средний уровень, а затем с ним сопоставляется уровень каждого месяца. Это процентное соотношение называется индексом сезонности IS:
Однако, полученные данные одного года в силу элемента случайности слишком ненадежные для выявления закономерности колебаний, поэтому чаще пользуются помесячными данными за ряд лет (в основном не менее 3 лет). Тогда для каждого месяца рассчитывается средняя величина уровня за 3 года, затем рассчитывается среднемесячный уровень для всего ряда, среднесуточный уровень и в заключение определяется индекс сезонности IS.
Алгоритм исчисления индексов сезонности: 1. Рассчитываются средние уровни для каждого месяца за ряд лет по данным за все годы исследуемого периода ( 2. Определяется общая средняя ( При расчете сезонных колебаний по абсолютным данным об объеме явления за каждый месяц величина При расчете сезонных колебаний на основе среднесуточных уровней
tk - число календарных дней каждого месяца.
3. Исчисляются индексы сезонности (IS) отношением средних из фактических уровней одноименных месяцев (
4. Совокупность исчисленных для каждого месяца годового цикла индексов сезонности (
7.4.2. Определение сезонных колебаний при наличии ярко выраженной тенденции к увеличению или уменьшению уровней тренда по годам, индексы сезонности (IS) определяются на основе методов, которые позволяют исключить влияние тенденции роста или спада явления (с использованием аналитического выравнивания имеющегося ряда динамики).
Алгоритм исчисления индексов сезонности: 1. Для каждого месяца (квартала) вычисляются средние уровни (
2. Для выявления общей тенденции ряда производится аналитическое выравнивание или сглаживание двенадцатимесячной скользящей средней ( 3. Для элиминирования определяются для каждого месяца средние из выравненных или сглаженных скользящих средних 4. Исчисляются индексы сезонности для каждого месяца (
5. Затем полученные данные о сезонной волне изображаются в виде линейной диаграммы.
Индексы сезонных колебаний представляют собой модель сезонной волны внутригодового цикла. Модель сезонной волны позволяет прогнозировать изменение явлений по внутригодовому циклу на будущее методом экстраполяции. Для сопоставления величины сезонных колебаний по нескольким предприятиям или периодам используется среднее квадратическое отклонение, исчисляемое по формуле:
IS - индекс сезонности каждого месяца; п - число месяцев в году (12).
Чем меньше среднее квадратическое отклонение, тем меньше величина сезонных колебаний.
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 748; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.110.182 (0.009 с.) |


 ,
, .
. = 0.
= 0. , можно определить a0 и a1 из системы уравнений для построения линейной модели:
, можно определить a0 и a1 из системы уравнений для построения линейной модели:


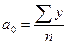

 и
и  .
.
 ), что позволяет избавиться от случайных колебаний месячных уровней по годам.
), что позволяет избавиться от случайных колебаний месячных уровней по годам. ) за весь исследуемый период.
) за весь исследуемый период. , где:
, где: .
. ) характеризует сезонную волну развития явления во внутригодовой динамике. Для получения наглядного представления о сезонной волне можно изобразить полученные данные в виде линейной диаграммы.
) характеризует сезонную волну развития явления во внутригодовой динамике. Для получения наглядного представления о сезонной волне можно изобразить полученные данные в виде линейной диаграммы. ).
). , т.е. исключения действия случайных факторов на основную тенденцию развития явления.
, т.е. исключения действия случайных факторов на основную тенденцию развития явления. ) по следующей формуле:
) по следующей формуле: .
. , где:
, где:


