
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели, характеризующие динамические рядыСодержание книги
Поиск на нашем сайте
1. Абсолютные приросты
базисные (накопленные) цепные (годовые) ∆
2. Темпы (коэффициенты) роста
базисные (накопленные) цепные (годовые)
3. Темпы (коэффициенты) прироста
базисные (накопленные) цепные (годовые)
4. Абсолютное значение 1% прироста
5. Коэффициент наращивания
6. Коэффициент опережения
7. Средний абсолютный прирост
8. Средний темп роста
9. Средний темп прироста
Тенденцию динамики характеризуют абсолютные, относительные и средние показатели. Показатели динамики, исчисленные по отношению к постоянной базе сравнения (у0), называются базисными, а показатели динамики, исчисленные по отношению к переменной базе сравнения, т.е. к предшествующему уровню(у 7.1.1. Абсолютные приросты или изменения базисные (накопленные) и цепные (годовые) обозначаются знаком Δ (дельта) и показывают, на сколько в абсолютном выражении уровень текущего периода больше (меньше) базисного:
у у у
Базисные (накопленные) приросты определяются путем вычитания из каждого уровня ряда у Цепные (годовые) приросты определяются путем вычитания из каждого уровня ряда у Между базисными и цепными абсолютными приростами существует взаимосвязь: сумма цепных абсолютных приростов равна базисному абсолютному приросту последнего периода ряда динамики S DУцепн = DУn.баз.(накопл.) 7.1.2. Темпы роста (базисные и цепные) характеризуют относительную скорость изменения уровня динамического ряда в единицу времени и показывают, сколько процентов уровень текущего периода составляет по отношению к уровню базисного периода или во сколько раз уровень текущего периода больше (меньше) уровня базисного периода. Темпы роста (или снижения) выражаются в процентах или коэффициентах и определяются по формулам:
Базисные темпы (или коэффициенты) роста характеризуют непрерывную линию развития явления. Цепные темпы (коэффициенты) роста характеризуют интенсивность развития явления для каждого исследуемого периода (месяца, квартала, года …). Между базисными и цепными коэффициентами или темпами роста также существует взаимосвязь: произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста, а частное от деления последующего базисного коэффициента роста на предыдущий равно соответствующему цепному коэффициенту роста:
7.1.3. Относительный прирост или темп прироста показывает на сколько процентов уровень текущего периода больше (меньше) уровня базисного периода, это есть отношение соответствующего абсолютного прироста к уровню, принятому за базу сравнения:
7.1.4. Абсолютное значение одного процента прироста (изменения) представляет собой отношение цепного годового абсолютного прироста к цепному годовому темпу прироста и показывает, какая абсолютная величина скрывается за одним процентом прироста; выражается в абсолютных единицах измерения:
Расчет этого показателя имеет экономический смысл только на цепной (годовой) основе.
7.1.5. Темп наращивания (изменения) определяется путем деления абсолютного прироста (годового) на уровень, принятый за постоянную базу сравнения:
На практике этот показатель часто всего используют в статистической информации для характеристики динамики социально-экономических явлений.
7.1.6. Коэффициент опережения показывает, во сколько раз один ряд динамики растет быстрее другого, и определяется сопоставлением коэффициентов роста или прироста двух рядов:
Рассчитывается при статистическом анализе и сопоставлении стохастически взаимосвязанных рядов динамики, характеризующих различные социально-экономические явления.
7.1.7. Среднегодовой абсолютный прирост определяется по следующим формулам:
7.1.8. Среднегодовой (среднеквартальный, среднемесячный…) темп роста характеризует интенсивность развития явления за длительный период времени и определяется по следующей формуле:
Уп – конечный уровень ряда динамики; Уо - базисный уровень ряда динамики; п - число периодов в изучаемом интервале времени, или число членов динамического ряда.
7.1.9. Среднегодовой (среднемесячный, среднеквартальный…) темп прироста можно исчислить на основе среднего темпа роста по формуле:
Показатели среднего темпа роста и среднего абсолютного прироста применяются при краткосрочном статистическом прогнозировании путем экстраполяции уровня развития изучаемого явления на ближайшее будущее.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 725; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |


 ∆
∆ 

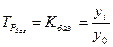


 =
= 



 или
или 
 =
= 

 .
. ) называются цепными.
) называются цепными. у
у  = у
= у 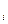 - у
- у  ;
; у
у  = у
= у 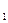 , у
, у  , …, у
, …, у  базисного или первоначального уровня (у0).
базисного или первоначального уровня (у0).

 = Тр.баз.- 100% или Тр.баз. - 1
= Тр.баз.- 100% или Тр.баз. - 1

 ,
,  - больший коэффициент или темп роста;
- больший коэффициент или темп роста; ,
,  - меньший коэффициент или темп роста;
- меньший коэффициент или темп роста; ,
, 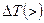 - больший коэффициент или темп прироста;
- больший коэффициент или темп прироста; ,
,  - меньший коэффициент или темп прироста.
- меньший коэффициент или темп прироста.



