
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели асимметрии и эксцесса распределенийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Для сравнительного анализа степени асимметрии нескольких распределений рассчитывается относительный показатель асимметрии (А s). Существует несколько видов расчетов коэффициента асимметрии, например по формуле:
М0 - центральный момент распределения, σ - среднее квадратическое отклонение. Величина показателя асимметрии (Аs)может быть положительной иотрицательной. Положительная величина показателя асимметрии указывает на наличие правосторонней асимметрии (более длинная ветвь вправо). Отрицательный знак показателя асимметрии говорит о наличии левосторонней асимметрии (более длинная ветвь влево). Величина асимметрии может изменяться от -1 до +1 (для одновершинных распределений). Чем больше абсолютная величина коэффициента асимметрии, тем больше степень скошенности вправо или влево. Принято считать, что если коэффициент асимметрии Аs меньше 0,25. то асимметрия незначительная, а если Аs свыше 0,5, то асимметрия значительная. При симметричном распределении Аs = 0, т.к. варианты равноудалены от Заостренность или крутизна графика распределения вычисляется с использованием центрального момента четвертого порядка по формуле:
M4 – центральный момент четвертого порядка,
При измерении асимметрии эталоном служит симметричное распределение, для которого А3 = 0. Для нормального распределения показатель асимметрии четвертого порядка равен 3 (А 4 = 3).
Для сравнения островершинности распределений в качестве эталонного выбирается нормальное распределение, которое сравнивается с фактическим и рассчитывается показатель эксцесса по формуле:
Эксцесс также может быть положительным и отрицательным. У высоковершинных (островершинных) распределений показатель эксцесса (Ех) имеет положительный знак (+), а у низковершинных (плосковершинных) – отрицательный знак (-). Предельным значением отрицательного эксцесса является значение Ех = - 2, величина положительного эксцесса является величиной бесконечной. Так как в нормальном распределении Средняя квадратическая ошибка эксцесса исчисляется по формуле:
n - число наблюдений. Оценка существенности показателей асимметрии и эксцесса позволяет сделать вывод о том, можно ли отнести данное распределение к типу нормального распределения. Распределения, близкие к нормальному распределению, встречаются при изучении самых различных явлений развития природы и общества. Показатели формы распределения Симметричное распределение (нормальное распределение)
При симметричной форме распределении частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой: Аs = 0 Правосторонняя асимметрия
Mo Me Положительная величина показателя асимметрии указывает на наличие правосторонней асимметрии: As > 0
Левосторонняя асимметрия
Отрицательная величина показателя асимметрии указывает на наличие левосторонней асимметрии: As < 0
Решение типовых задач 5.7.1. По данным распределения возраста студентов одного из факультетов ВУЗа определимразмах распределения, среднее линейное отклонение, дисперсию и среднее квадратическое отклонение.
Решение: Прежде всего находим самое маленькое значение возраста студентов Xmin = 17 лет и самое большое Хmax = 23 года (графа А таблицы). Находим разницу между максимальным и минимальным значением признака и получаем величину размаха, которая составляет:
R = 23 – 17 = 6 лет.
Для проведения дальнейших вычислений показателей вариации проведем дополнительные расчеты и запишем их в имеющуюся таблицу: - определяем произведение значений признака(x - рассчитаем среднюю величину по формуле средней арифметической взвешенной:
Для расчета среднего линейного отклонения находим абсолютное отклонение значений признака (x Вычисляем произведения отклонений Делим эту сумму (
Таково в среднем отклонение вариантов признака от их средней величины. Возведем в квадрат отклонения индивидуальных значений признака от их средней Затем квадрат отклонений Разделим эту сумму
Извлечем корень квадратный из дисперсии и получим величину среднего квадратического отклонения:
Таким образом, каждое индивидуальное значение возраста студентов отклоняется от их средней величины на 1,63 года.
5.7.2. Дисперсия признака равна 600. Объем совокупности равен 10. Сумма квадратов индивидуальных значений признака равна 6250. Найдитесреднюю величину совокупности.
Решение: Для нахождения средней величины воспользуемся методом отсчета от условного нуля или методом моментов:
Тогда: Средняя величина признака:
5.7.3. Для характеристики однородности совокупности следует вычислить показатели вариации: дисперсию, среднее квадратическое отклонение, коэффициент вариации (вычисления выполнить в таблице).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 4360; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.008 с.) |

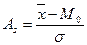 , где:
, где: - средняя величина ряда распределения,
- средняя величина ряда распределения,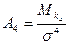 , где:
, где: среднее квадратическое отклонение в четвертой степени.
среднее квадратическое отклонение в четвертой степени.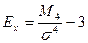
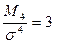 , следовательно, для нормального распределения показатель эксцесса равен нулю (Ех = 0).
, следовательно, для нормального распределения показатель эксцесса равен нулю (Ех = 0).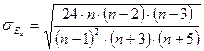 , где:
, где: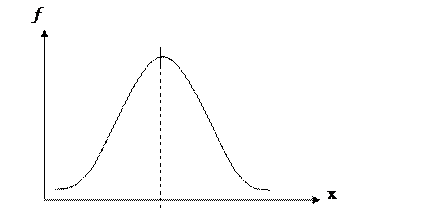
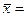 Mo=Me
Mo=Me


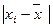
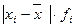
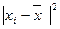
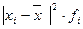
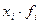
 ) на соответствующие веса (fi) (графа 6). В итоге получаем сумму, равную 13060.
) на соответствующие веса (fi) (графа 6). В итоге получаем сумму, равную 13060. =
= 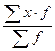 =
= 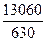 = 20,7 года.
= 20,7 года.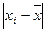 (графа 2).
(графа 2).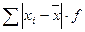 ) на сумму весов (fi), чтобы получить искомую величину
) на сумму весов (fi), чтобы получить искомую величину 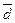 :
: =
= 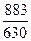 = 1,4 года.
= 1,4 года.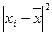 и запишем результат в графу 4 таблицы.
и запишем результат в графу 4 таблицы.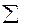 (x
(x  f на сумму весов
f на сумму весов  =
= 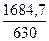 = 2,67
= 2,67 =
= 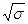 =
= 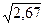 = 1,63 года
= 1,63 года =
= 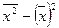 , где
, где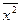 - средняя арифметическая из квадратов индивидуальных значений признака;
- средняя арифметическая из квадратов индивидуальных значений признака;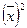 - квадрат среднего значения признака.
- квадрат среднего значения признака.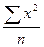 =
= 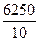 = 625.
= 625.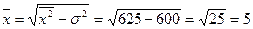 .
.


