
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристики структуры распределенияСодержание книги
Поиск на нашем сайте Мода- величина признака, кот встречается в ряду распределения чаще всего. Бимодальное распред. -распределение значений признака Унимодальное -одна ярко выраженная мода Если ряд ранжированный-переводим его в дискретный. Мода в дискретном ряду считается- считаем частоту по каждому признаку и выбираем наиболее часто встречаемый. Медиана —значение, расположенное посередине ранжированного вариационного ряда. Порядковый номер(ранг)= (n+1)/2 Квантили - значения признака, которые делят совокупность на 4 равные по числу единиц части. Квинтили, деление на 5 частей Сикстили- деление на 6 частей Децили- на 10 Перцентли -10 Нормальное распределение теоретически гладкая гистограмма. Идеальный набор данных, в которых большинство чисел сконцентрировано в средней части диапазона значений. Значения наблюдений не ограничены по своей величине. ü диапазон ±1 S - 68,26% площади (значений). ü диапазон ±2 S – 95,44% площади (значений). ü диапазон ±3 S - 99,72% площади (значений). Расстояние по горизонтальной оси, измеренное в единицах стандартного отклонения от среднего арифмет-го всегда даёт одинаковую площадь под кривой. Показатели формы распределения: Асимметрия.
Правосторонняя As > 0; Левосторонняя As < 0 Эксцесс.
Асимметрия НР=0 и Эксцесс=0 Более вытянутая вершина графика эксцесс >0, более пологий график эксцесс<0
Показатели изменчивости. 1.Размах - абсолютная разность между максимальным и минимальным значениями признака в изучаемой совокупности. R=Хmax-Хmin. Размах исп-ся для поиска ошибок в данных. Акцентируется внимание на экстремальных значениях. 2. Среднее линейное отклонение: простая взвешенная
3. Среднее квадратическое отклонение = стандартное отклонение. Отражает типичное расстояние между средним значением и отдельными значениями набора данных (если знач.пост.,то изменчивость=0). Показывает степень случайности в расположении отдельных значений относительно их среднего. Простое и взвешенное стандартное отклонение. для выборки Простое Взвешенное
для ген. сов-ти Простое Взвешенное
4.Дисперсия- квадрат ср.квадр.откл.
(квадрат среднего-среднее квадрата)
5.Коэф-ент осцилляции. к-т осцилляции (относительный размах вариации)
6.Коэф-нт вариации - мера относительного разброса случайной величины; показывает, какую долю среднего значения этой величины составляет ее средний разброс.
Vσ< 33% => совокупность однородная
Задача сглаживания эмпирического распределения заключается в определении вероятности попадания случайной величины на заданный интервал. Вероятность того, что значение попадет в интервал = площади соответствующей области под кривой НормРасп. Стандартизованная теоретическая кривая НР:
Таблица нормального распред-я = таблица Z значений Правило определения вероятностей случайной величины наз-ся распределением вероятностей. Площадь в табл. НР – это вероятность. Критерии согласия - критерии для проверки гипотезы о нормальности распределения или оценка близости эмпирических и теоретических частот.
df=(r-1)*(c-1) Количество степеней свободы - количество значений в распределении, которые свободны для изменений. Если χэмп2 < χкр0,012 ® Критерий согласия А.Н. Колмогорова используется при определении максимального расхождения между частотами эмпирического и теоретического распределения. λ= D/√n, где D -максимальная разность накопленных теоретических f’ и экспериментальных f частот. Если λ<0,3 => P(λ)=1 => отклонения между теоретическим и эмпирическим нет Критерий согласия В.И. Романовского
K – число степеней свободы R < 3 => расхождение между теоретическим и эмпирическим – случайное R > 3 => неслучайное, существенное Критерий Ястремского.
r – число групп
lфакт < 3 => расхождение между теоретическим и эмпирическим – случайное lфакт > 3 => неслучайное, существенное Θ = 0,6 при числе групп< 20 Выбор вида распределения. Нормальное распределение – непрерывные величины
Характеристики: 1.Среднее или ожидаемое значение дискретной случайной величины X:
2.Стандартное отклонение дискретной случайной величины X (риск, неопределенность ситуации)
Биномиальное распределение - если количество наступлений событий выражается как процент от общего количество возможностей. Применение: -В каждой из n попыток вероятность наступления события π одна и та же; -Все попытки независимы друг от друга. Примеры Количество дефектных изделий среди 10 единиц выпущенной продукции; Количество женщин, работающих в отделе со штатом 75 человек… Распределение Пуассона -распределение дискретной величины, которое зависит только от ожидаемого среднего количества наступления событий Применение: события происходят: -Случайно -Независимо -Среднее число наступления события с ростом числа попыток не изменяется Примеры Количество заказов, которые фирма получит завтра; Количество дефектов в произведенной продукции; Экспоненциальное распределение- Непрерывное распределение с сильной асимметрией Применение: события происходят: -Случайно -Независимо -С постоянной частотой Время ожидания между 2-мя последовательно наступающими событиями Примеры Длительность типичного телефонного разговора; Время безотказной работы кинескопа
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 352; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.36.9 (0.009 с.) |





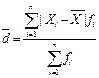
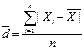








 (станд.откл.)
(станд.откл.)
 1.Критерий согласия Пирсона, который можно представить как сумму отношений квадратов расхождений между f' и f к теоретическим частотам:
1.Критерий согласия Пирсона, который можно представить как сумму отношений квадратов расхождений между f' и f к теоретическим частотам:




