
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие, предмет, задачи статистики.Содержание книги
Поиск на нашем сайте
ВОПРОСЫ К ЭКЗАМЕНУ ПО КУРСУ «СТАТИСТИКА»
1. Основные понятия статистики. 1.1. Предмет статистики. Цели. Составные части. 1.2. Статистическая закономерность. Закон больших чисел. 1.3. Статистическая совокупность. Единица статистической совокупности. 1.4. 4 этапа статистического анализа. 1.5. Виды рядов. 1.6. Классификация признаков. 1.7. Статистические показатели. Абсолютные и относительные показатели. 2. Выборки. 2.1. Виды выборок. 2.2. Способы формирования выборок. 2.3. Репрезентативность. 2.4. Ошибка выборки. 3. Наблюдения 3.1. План статистического наблюдения. 3.2. Виды статистического наблюдения. 3.3. Контроль данных. 3.4. Выбросы и стратегия их обработки. 4. Вариационные ряды. 4.1. Понятие и виды вариационных рядов. 4.2. Построение вариационных рядов и их структурные характеристики (медиана, мода, квартили, квинтили…). 4.3. Графическое изображение вариационных рядов. 4.4. Показатели размера и интенсивности вариации (размах, среднее линейное отклонение, простое и взвешенное стандартное отклонение, дисперсия для выборки и ГС, коэффициенты осцилляции и вариации). 5. Методы средних величин. 5.1. Средние арифметические и их свойства. 5.2. Степенные средние. 5.3. Правило мажорантности средних. 6. Распределение наблюдений. 6.1. Построение нормального распределения по эмпирическому ряду. 6.2. Основные параметры нормального распределения. 6.3. Показатели формы распределения (центральные моменты, показатели асимметрии, показатель эксцесса). 6.4. Z-распределение. 6.5. Стандартная ошибка среднего (простая, для малой ГС, для стратифицированной выборки). 6.6. Доверительный интервал, определение необходимого размера выборки 6.7. Доказательство «нормальности» распределения. 6.8. Биномиальное распределение и его характеристики. 6.9. Распределение Пуассона и его характеристики. 6.10. Экспоненциальное распределение и его характеристики. 7. Гипотезы. 7.1. Статистическая проверка гипотез. Классы гипотез. 7.2. Классификация методов проверки гипотез. Понятие числа степеней свободы. 7.3. Ошибка 1 рода и ошибка 2 рода. 7.4. T-статистика и t-тест. 7.5. Критерии согласия, назначение и примеры: Критерии Колмогорова-Смирнова, Романовского, Ястремского. 7.6. Непараметрические методы проверки гипотез (Критерий Розенбаума, критерий Манна-Уитни, критерий χ2 Пирсона).
8. Корреляционный анализ. 8.1. Понятие корреляции. Виды корреляционной связи (парная линейная, параболическая, гиперболическая, множественная, корреляция рангов). 8.2. Коэффициенты корреляции. 8.3. Оценка надежности коэффициента корреляции. 8.4. Измерение связи неколичественных признаков (К-нт ассоциации, к-нт контингенции, к-нт сопряженности Пирсона, к-нт сопряженности Чупрова, к-нт корреляции рангов Спирмена, к-нт корреляции Фехнера). 9. Регрессионный анализ. 9.1. Цели, виды. 9.2. Ошибка выбранной модели. 10. Кластерный анализ. 10.1. Цели. Евклидово расстояние. Стандартизация. 10.2. Методы объединения объектов. 10.3. Дендрограмма. Основные характеристики кластеров. 11. Факторный анализ: цели, этапы, методы вращения факторных нагрузок. 12. Дисперсионный анализ: цели, область применения, основные методы. 13. Графические методы анализа данных. 14. Динамические ряды. 14.1. Основные понятия, элементы, виды. 14.2. Модель динамического ряда. 14.3. Исключение случайных колебаний (Методы механического сглаживания). 14.4. Методы аналитического выравнивания. 14.5. Авторегрессионная модель. 14.6. Выбор адекватной модели прогнозирования. 14.7. Сезонные колебания (Индекс сезонности, поправка на сезон). 14.8. Показатели изменения уровней динамических рядов (базисные, цепные, абсолютные, относительные и средние характеристики тенденции динамики). 15. Контроль качества. 15.1. Понятие процесса. Анализ процесса. 15.2. Диаграмма Парето. 15.3. Анализ гистограмм. 15.4. Контрольные карты Шухарта. 15.5. Индекс пригодности процесса. 15.6. Стратегии совершенствования процесса. 16. Индексы. 16.1. Понятие индекса. Назначение. Составные части индекса. Индивидуальные и сводные индексы, средние взвешенные и агрегатные индексы. 16.2. Индексы цен (индивидуальный), товарооборота, физического объема продукции, себестоимости продукции. 16.3. Индексы Ласпейреса и Пааше. Формулы и назначение. 16.4. Агрегатный и территориальный индексы цен. Средний взвешенный индекс цен. 16.5. Статистика доходов. 16.5.1. Уровень жизни населения. Понятие и виды. 16.5.2. Основные показатели уровня жизни (НДД, РаспДД, РеалДД, СДД, уровень покупательской способности). 16.5.3. Коэффициент дифференциации доходов (Децильный КДД, к-нт фондов, к-нт Джини, кривая Лоренца). 16.5.4. Прожиточный минимум, коэффициент бедности. 16.6. Статистика потребления населением товаров и услуг. 16.6.1. Структура товаров и услуг. 16.6.2. Индекс объема потребления. 16.6.3. Коэффициент эластичности. 16.6.4. Статистика инфляции. Дефлятор ВВП, Индекс инфляции, Норма инфляции, Темп инфляции, Годовой индекс инфляции. 16.7. Статистика населения и занятости 16.7.1. Показатели естественного прироста. Коэффициент рождаемости, коэффициент смертности, к-нт естественного прироста. 16.7.2. Статистика миграции. Миграционный прирост, миграционный отток, к-нт прибытия, к-нт выбытия, к-нт миграционного прироста, к-нт интенсивности миграционного оборота, к-нт эффективности миграции. 16.7.3. Занятость. К-нт занятости, к-нт безработицы. 16.7.4. Индекс развития человеческого потенциала. 16.8. Статистика национального богатства – Это тема САМОСТОЯТЕЛЬНОГО изучения. Необходимый минимум находится по адресу: http://www.hi-edu.ru/e-books/xbook096/01/index.html?part-014.htm – Тема 14. 16.8.1. Состав национального богатства. 16.8.2. Статистика основных фондов. К-нт годности, к-нт износа, к-нт обновления. Показатель фондоотдачи. Показатель фондоемкости. 16.8.3. Статистика материальных оборотных фондов. Обеспеченность производственными запасами. Средний остаток оборотных фондов. К-нт оборачиваемости. К-нт закрепления оборотных фондов.
Примеры задачек к экзамену:
ЗАДАЧА 1.
Пользуясь формулой Стерджесса, определите интервал группировки сотрудников фирмы по уровню доходов, если общая численность сотрудников составляет 20 человек, а минимальный и максимальный доход соответственно равен 500 и 3000 у.е. ЗАДАЧА 2. Производство сахарного песка в РФ в январе – апреле 2011г. характеризуется следующими данными:
Рассчитайте абсолютные и относительные показатели динамики. ЗАДАЧА 3. Сколько клиентов студенческой столовой нужно опросить, если исследуется сумма, которые студенты готовы потратить на комплексный обед. Ошибиться Вы хотите не более чем на 25 рублей, а предварительная оценка минимальной суммы равна 60 рублям, максимальной – 200 рублям. ЗАДАЧА 4. Имеются следующие данные об успеваемости студентов ВУЗа:
Определите долю отличников (в процентах) в общей численности студентов ВУЗа. ЗАДАЧА 5. Имеется следующий ряд распределения телеграмм, принятых отделением связи по числу слов:
Рассчитайте абсолютные и относительные показатели вариации. Понятие, предмет, задачи статистики. Статистика - искусство и наука сбора и анализа данных. Предмет статистики - массовые варьирующиеся явления. Варь приз.- приз, меняющ свое знач при переходе от одной совок к др. Задача стат - установить общ св-ва единиц совок-ти, изучить имеющиеся взаимосвязи и законом-ти развития. Достигается это с помощью расчёта стат показат и их анализа Основные этапы статистического анализа. 1.Планирование сбора данных- нужно гарантировать, что сбор данных будет беспристрастным, все объекты имеют шанс быть собранными. 2.Сбор данных Способы сбора данных: 1.опрос,анкетирование, 2.наблюдение, 3.эксперимент, 4.изучение офиц.источников. 3.Систематизация собранных данных. Первичная оценка данных и оценки неизвестных величин 4.Проверка гипотезы Закон больших чисел если эксперимент проведен много раз, относит. частота близка к вер-ти. Пр:Монету подбросили. Вер-ть падения решкой? Р=1/2=0,5 (50%) Df: Вер-ть события А=кол-во благопр.исходов/общее кол-во исходов Вер-ть соб А(с чертой)=1-Вер.соб А *Формула Байеса: P(A:B) = P(B:A) * P(A) / ((P(B:A) * P(A) +P(B: Ā) * P(Ā)) Статистич сов-ть сов-ть объектов или явлений одного и того же вида, объединенных наличием общих признаков. Единица стат сов-ти - первич. элемент статистич сов-ти, являющийся носителем признаков, подлежащих исследованию. Признак -св-во, присущее единице сов-ти. Стат.показатель -обобщающая хар-ка всей сов-ти Признаки конкретное св-во единиц совок-ти, которое можно пронаблюдать и измерить. 1-по стадии исследования (первичный, вторичный) 2-по отношению к исследуемому объекту (прямые -характер св-ва, непосредственно присущие объекту исслед-я; косвенные -хар.св-ва, присущие не самому объекту исследования, а объектам, связанным с объектом исследования) 3-по форме выражения (количестенные (непрерывные - могут приним любое знач, дискретные - могут приним определённые заранее известные значения) качественные (порядковые; номинальные) 4-по хар-ру взаимосвязи (факторные влияют на рез-т,; результативные) 5-по хар-ру вариации (альтернативные - призн, кот приним 2 значен; с кол-вом вариантов >2-х). Абсолютные величины - показатель, представляющий собой количеств. хар-ки изучаемых явлений. Относительные величины -показатели, получаемые сопоставлением абсолютн. или относит. величин. Виды:ОВ структуры-определ.долю части в общем V сов-ти(часть единиц сов-ти/общий V сов-ти) § ОВ координации –соотношение между 2-мя частями исследуемой сов-ти (одна часть сов-ти/др.часть этой же сов-ти, обычно в числит.меньш.число) § ОВ выполн.плана (фактич.ур-нь явления/плановый ур-нь явления) § ОВ сравнения-соотношение одноименных абсолютных показателей, относящихся к разным объектам, но к одному и тому же времени) (одна сов-ть/др сов-ть) Одноименные!!! § ОВ интенсивности-отношение между разноименными абсол.величинами (одна сов-ть/др сов-ть) Разноименные!!! (л.молока/поголовье скота) Статистическое наблюдение § сбор сведений по заранее разработанному плану. Реализуется посредством отчетности-по установл.формам, в установленный срок; посредством спец.организ.обследований). § Виды статистического наблюдения § 1)По охвату единиц сов-ти (сплошное/несплошное). § 2) По времени регистрации (текущее/единовременное/ периодическое). § 3)По способу регистрации: корреспондентский, экспедиционный, анкетный, саморегистрация, явочный § 4) По источникам получения информации (наблюдение/Документальный способ/Опрос) § План статистического наблюдения § 1)Программно-методологическая часть: 1. Цель и задачи 2. Объект и единицы 3. Время начала - окончания 4. Программа § 2)Организационная часть: 1. Сроки и место 2. Кадровое обеспечение 3. Организация сбора данных 4. Технология обработки 5. Орг.-хоз. мероприятия § § 2. Выборочное наблюдение § разновидность наблюдения, охватывает отобранную часть единиц генеральной совокупности. Цель - по отобранной части единиц дать характеристику всей генеральной совокупности. § Выб. набл. должно быть репрезентативным. Репрезентативность - каждое св-во и в выборке и в генер.совокупности имеет одинаковые частоты. § Способы отбора: 1)Перепись(n=N), 2)Без возврата или с возвратом, 3)Неслучайная или случайная, 4)Стратифицированная (исп-ем естеств.подгруппы-страты) § § 9. Ошибки наблюдения: § 1. Репрезентативности- соотношение результатов не совпадает с тем, что есть; § 2. Регистрации: преднамеренные -непреднамеренные: а) случайные б) систематические § Контроль данных: Логический (может поставить под сомнение правильность полученных данных, поскольку основан на логической взаимосвязи между признаками) и Арифметический (для проверки итоговых сумм). § Выбросы. 1. ошибки (некорректно введённые данные), 2. отличающиеся значения (данные не относятся к исследуемому набору/исключительное явление).
При исключении выбросов всегда объяснять причину!
Группировка распределение единиц по группам т.о., чтобы различия между единицами отнесенными к одной группе были <, чем различия между единицами отнесенными к разным группам. Статист. представление инф-ции: -статистические таблицы -статист.графики
3. Вариация многообразие значений признака у единиц данной совокупности. Вариационный ряд - упорядоченное распределение единиц совокупности (ряд распределения). Показатели вариации - числовые характеристики статистического распределения, демонстрирующие степень рассеяния наблюдаемых значений измеряемого показателя относительно их среднего значения. Чем выше показатели вариации, тем больший наблюдается разброс в значениях измеряемого показателя, и тем менее надежны результаты измерений. Размах, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэф-т осцилляции, коэф-т вариации. 5 базовых показателей вариационного ряда: min, max,1-й квартиль, медиана, 3-й квартиль. . Виды вариационных рядов Ранжированный (если объектов не много) Ранжирование позволяет легко разделить кол-ые данные по группам, сразу обнаружить наим.и наиб.значения признака, выделить значения, кот.чаще всего повторяются.
Дискретный (если объектов много, а признак принимает небольшое число возм-ых значений). Интервальный (если признак может принимать большое количество значений или эти значения могут быть дробными-объединяем значения признака в интервал).
Интервальный ряд если признак может принимать большое количество значений или эти значения могут быть дробными- объединяем значения признака в интервал. Формула Стерджеса:К=1+3,322lg(n) i=R/K R=(xmax-xmin) (размах) K – количество интервалов (групп), n – кол-во единиц совокупности, i – величина интервала. 5 Средняя величина обобщающая величина изучаемого признака совокупности 1.(Простое)Выборочное среднее = сумма значений элементов данных/количество элементов данных. Для ранжированного ряда
для генеральной совокупности- μ
Взвешенное среднее
Степенные средние. Виды: Простые Взвешенные
(k-степень ср. величины) Среднее гармоническое (К = -1): простое взвешенное
Применяем для оценки средних затрат труда, времени, расстояния, материалов на единицу продукции. Среднее геометрическое (К=0): простое взвешенное
П -произведение Применяем для интегрального сравнения объектов Среднее квадратическое (К=2): простое взвешенное
Для исчисления среднего квадратического отклонения. Среднее кубическое (К=3 ): простое взвешенное
Правило мажорантности средних: (Хгарм<Xгеом<Харифм<Хквадр<Хкуб)
6. Ряды распределения В зависимости от того, какой признак (количественный или качественный) взят за основу группировки данных, различают: Атрибутивный ряд распределения - качественный признак Вариационный - количественныйу признак. Построить вариационный ряд - значит упорядочить количественное распределение единиц совокупности по значениям признака, а затем подсчитать числа единиц совокупности с этими значениями. Вариационные ряды: Ранжированный (если объектов не много) Дискретный (если признак принимает небольшое число значений). В основу построения положены признаки с прерывными изменениями (дискретные признаки-кол-во детей в семье, число работников на предпр-ии,.Строится табл., где каждая строчка значения признака- кол-во единиц совокупности с данным значением признака.Табл.состоит из 2-х граф. В 1-ой-указ-ся конкретное значение признака, а во 2-ой-число единиц сов-ти с опред.значением признака. Интервальный (если признак может принимать большое количество значений или эти значения могут быть дробными- объединяем значения признака в интервал). Если признак имеет непрерывное изменение (размер дохода, стаж работы). Групповая таблица имеет 2 графы. В 1-ой указ-ся значение признака в интервале «от-до»(вар-ты), во 2-ой-число единиц, входящих в интервал(частота). Формула Стерджеса К=1+3,322lg n i=R/K R=(xmax-xmin) K – количество интервалов, n – кол-во единиц совокупности, i – величина интервала. . Характеристики центра распределения Средняя величина - обобщающая величина изучаемого признака совокупности, характеризующая типичный уровень совокупности. Мода- величина признака, кот встречается в ряду распределения чаще всего. Бимодальное распред. -распределение значений признака Унимодальное -одна ярко выраженная мода Если ряд ранжированный-переводим его в дискретный. Мода в дискретном ряду считается- считаем частоту по каждому признаку и выбираем наиболее часто встречаемый. Медиана —значение, расположенное посередине ранжированного вариационного ряда. Порядковый номер(ранг)= (n+1)/2 Соотношение среднего, моды и медианы: Хср<Ме<Мо- левосторонняя асимметрия Мо<Ме<Хср- правосторонняя Мо=Ме=Хср- классическое нормальное распределении.
Нормальное распределение теоретически гладкая гистограмма. Идеальный набор данных, в которых большинство чисел сконцентрировано в средней части диапазона значений. Значения наблюдений не ограничены по своей величине. ü диапазон ±1 S - 68,26% площади (значений). ü диапазон ±2 S – 95,44% площади (значений). ü диапазон ±3 S - 99,72% площади (значений). Расстояние по горизонтальной оси, измеренное в единицах стандартного отклонения от среднего арифмет-го всегда даёт одинаковую площадь под кривой. Показатели формы распределения: Асимметрия.
Правосторонняя As > 0; Левосторонняя As < 0 Эксцесс.
Асимметрия НР=0 и Эксцесс=0 Более вытянутая вершина графика эксцесс >0, более пологий график эксцесс<0
Показатели изменчивости. 1.Размах - абсолютная разность между максимальным и минимальным значениями признака в изучаемой совокупности. R=Хmax-Хmin. Размах исп-ся для поиска ошибок в данных. Акцентируется внимание на экстремальных значениях. 2. Среднее линейное отклонение: простая взвешенная
3. Среднее квадратическое отклонение = стандартное отклонение. Отражает типичное расстояние между средним значением и отдельными значениями набора данных (если знач.пост.,то изменчивость=0). Показывает степень случайности в расположении отдельных значений относительно их среднего. Простое и взвешенное стандартное отклонение. для выборки Простое Взвешенное
для ген. сов-ти Простое Взвешенное
4.Дисперсия- квадрат ср.квадр.откл.
(квадрат среднего-среднее квадрата)
5.Коэф-ент осцилляции. к-т осцилляции (относительный размах вариации)
6.Коэф-нт вариации - мера относительного разброса случайной величины; показывает, какую долю среднего значения этой величины составляет ее средний разброс.
Vσ< 33% => совокупность однородная
Задача сглаживания эмпирического распределения заключается в определении вероятности попадания случайной величины на заданный интервал. Вероятность того, что значение попадет в интервал = площади соответствующей области под кривой НормРасп. Стандартизованная теоретическая кривая НР:
Таблица нормального распред-я = таблица Z значений Правило определения вероятностей случайной величины наз-ся распределением вероятностей. Площадь в табл. НР – это вероятность. Критерии согласия - критерии для проверки гипотезы о нормальности распределения или оценка близости эмпирических и теоретических частот.
df=(r-1)*(c-1) Количество степеней свободы - количество значений в распределении, которые свободны для изменений. Если χэмп2 < χкр0,012 ® Критерий согласия А.Н. Колмогорова используется при определении максимального расхождения между частотами эмпирического и теоретического распределения. λ= D/√n, где D -максимальная разность накопленных теоретических f’ и экспериментальных f частот. Если λ<0,3 => P(λ)=1 => отклонения между теоретическим и эмпирическим нет Критерий Ястремского.
r – число групп
lфакт < 3 => расхождение между теоретическим и эмпирическим – случайное lфакт > 3 => неслучайное, существенное Θ = 0,6 при числе групп< 20 Выбор вида распределения. Нормальное распределение – непрерывные величины
Характеристики: 1.Среднее или ожидаемое значение дискретной случайной величины X:
2.Стандартное отклонение дискретной случайной величины X (риск, неопределенность ситуации)
Биномиальное распределение - если количество наступлений событий выражается как процент от общего количество возможностей. Применение: -В каждой из n попыток вероятность наступления события π одна и та же; -Все попытки независимы друг от друга. Примеры Количество дефектных изделий среди 10 единиц выпущенной продукции; Количество женщин, работающих в отделе со штатом 75 человек… Распределение Пуассона -распределение дискретной величины, которое зависит только от ожидаемого среднего количества наступления событий Применение: события происходят: -Случайно -Независимо -Среднее число наступления события с ростом числа попыток не изменяется Примеры Количество заказов, которые фирма получит завтра; Количество дефектов в произведенной продукции; Экспоненциальное распределение- Непрерывное распределение с сильной асимметрией Применение: события происходят: -Случайно -Независимо -С постоянной частотой Время ожидания между 2-мя последовательно наступающими событиями Примеры Длительность типичного телефонного разговора; Время безотказной работы кинескопа Стандартная ошибка выборки. Стандартная ошибка среднего:
Поправка для малой ГС Расчет объема выборки. Размер выборки зависит: -от размера ГС -от точности кот. хотим получить.
σ ≈ N/6 t-уровень достоверности, критическое значение для которого считаем t=2,57 для 0,99, t=1,96 для 0,95. Пример: Сколько человек нужно опросить, если всего у компании 200 постоянных клиентов? Чем точнее хотим получить результат, т.е чем меньше разница между средним Гс по выборке и ГС, тем больше выборка. Если объем выборки составляет 10% и больше от объема ГС, то рассчитывается окончательная коррекция совокупности:
n — объем выборки до применения окончательной коррекции; nкорр— объем выборки после применения окончательной коррекции. Пример: Сколько человек нужно опросить, если всего у Вашей компании 50 постоянных клиентов?
Если изучаемая статистика является не средним, а долей: 29. Гипотеза недоказанное утверждение, предположение или догадка. Можно проверить гипотезы:-о различиях между группами \выборками, -о различиях между признаками, -о зависимостях между признаками, -о форме распределения. Н0 – гипотеза об отсутствии различий (нулевая). Н1 – гипотеза о значимости различий (альтернативная). Гипотезы: Направленные: Н0 (рост мужчин не больше, чем женщин), Н1 (муж. выше жен.) Ненаправленные:Н0 (рост муж. и жен. одинаковый), Н1 (рост муж. и жен. разный) Проверка гипотезы – решающее правило, обеспечивающее принятие истинной и отклонение ложной гипотезы с высокой вероятностью. Критерий проверки гипотезы: решающее правило, обеспечивающее принятие истинной и отклонение ложной гипотезы с высокой вероятностью: 1.Непараметрические (в формуле исп-ся частоты и ранги)Ранжировать-упорядочивать. 2. Параметрические (в формуле исп-ся параметры распределения, среднее и станд.откл.) Критерий Розенбаума. Цель: Оценка различий между 2 выборками в уровне признака. Условие: Количество измерений в каждой выборке n1, n2 ≥ 11; n1 ≈ n2 Qэмп = S1 + S2 Алгоритм: 1. Упорядочить значения по степени возрастания признака. Выборка 1значения предполагаются >. 2. Определить макс значение в выборке 2. 3. Подсчитать количество значений в выборке 1, которые выше макс значения выборки 2: S1 4. Определить мин значение в выборке 1. 5. Подсчитать количество значений в выборке 2, которые ниже мин значения выборке 1: S2 6. Qэмп = S1+S2 7. По таблице определить критические значения Q для n1, n2. Если Q эмп >= Q 0,05, H0 отвергается. 8. При n1, n2 >=26 H0 отвергается, если Qэмп = 8 (p<=0,05), =10 (p<=0,01).
Критерий Манна-Уитни. -Оценка различий между двумя выборками по уровню количественно измеренного признака. Размеры выборок: n1, n2 ³ 3 или n1=2, n2 ³ 5; n1, n2 ≤ 60
Uэмп < U кр0,05 ® H1 Uэмп≥ U кр0,01® H0 Параметрический метод. Критерий χ2 Пирсона. Цель: 1. Сопоставление эмпирического распределения с теоретическим – Разница между фактическими и ожидаемыми частотами. 2. Сопоставление 2-х и более эмпирических распределений.
Хэмп² ≥ Хкр0,05² ® H1, χэмп2 < χкр0,01² ® H0 df=(r-1)*(c-1) Количество степеней свободы - количество значений в распределении, которые свободны для изменений.. Особые случаи: 1.Если признак принимает 2 значения: k=2(2 строки в таблице) 2. Если признак варьируется в широком диапазоне: укрупняйте разряды признаков. 32. Виды связей между признаками Статистическая - связь, где воздействие отдельных факторов проявляется только как тенденция. Корреляция – мера зависимости переменных. Сила взаимосвязи данных. (Коэф-ты Пирсона, Фехнера, Спирмэна)
33. Показатели тесноты парной связи Коэф-т корреляции Пирсона:
Интерпретация Пирсона: Отклонение признака-фактора от его среднего на величину стандартного отклонения в среднем приводит к отклонению признака-результата от своего среднего на величину r его стандартного отклонения. Коэффициент корреляции Пирсона -1 ≤ Rxy ≤ 1. Rxy = -1Строгая отрицательная корреляция, Rxy = 1Строгая положительная корреляция, Rxy = 0Отсутствие корреляции 0,7 ≤ | Rxy | ≤ 1 Сильная корреляция, 0,5 ≤ | Rxy | ≤ 0,7 Средняя корреляция, 0,3 ≤ | Rxy | ≤ 0,5 Слабая корреляция, 0 ≤ | Rxy | ≤ 0,3 Незначимая корреляция Меры тесноты парной связи:
C – количество совпадающих знаков отклонений от средних H – количество несовпадающих знаков отклонений от средних C + H = n Алгоритм расчета: -расчет среднего для X и Y -сравнение индивид.значений xi и yi со средними значениями с обязат.указаниями знака (+ или -). Если совпад., то относим к «С», если не совпад.,то к «Н». -считаем кол-во совпад.или несовпад. Коэффициент Спирмена: Не параметр.показатель, с помощью кот.пытаемся выявить связи между рангами соответ.величин.
где di – разность рангов по обоим признакам для каждого объекта.
Множественная корреляция Корреляция – мера зависимости переменных. Сила взаимосвязи данных. Меры тесноты парной связи: Коэф-т Пирсона, Спирмена, Фехнера. Множественная корреляция.
Использование метода множественной корреляции позволяет обнаружить объедин. эффект. влияния всех независимых переменных к зависимой. Корреляционный анализ показывает тесноту связи, только если связь линейная. Доказательство линейности связи. Чтобы подтвердить линейный характер связи необходимо сравнить η² и R². Корреляционное отношение
степень аппроксимации
R² коэфф.детерминации,указывает, какая доля вариации результативного признака объясняется влиянием всех X – переменных.
35. Регрессия – это предсказание значения одного признака на основе значения другого.Регрессионный анализ проводится при наличии корреляционной связи между признаками. Оценка ошибки выбранной математической модели.
y – эмпирическое значение, y* - теоретическое значение, p – число параметров уравнения. Доказательство линейности связи. Чтобы подтвердить линейный характер связи необходимо сравнить η² и R². Корреляционное отношение
36. 37. Парная линейная рег-я: Y = Сдвиг + Наклон * X; Y = a + b*X Параметры уравнения парной линейной регрессии вычисляются с помощью метода наименьших квадратов.
Сумма квадратов отклонений эмпирических значений зависимой переменной от вычисленных по уравнению регрессии должна быть мин. Параметры линейной регрессии находятся из системы:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 338; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.227.73 (0.015 с.) |



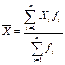

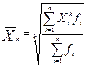




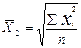








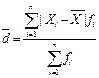
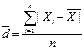








 (станд.откл.)
(станд.откл.)
 1.Критерий согласия Пирсона, который можно представить как сумму отношений квадратов расхождений между f' и f к теоретическим частотам:
1.Критерий согласия Пирсона, который можно представить как сумму отношений квадратов расхождений между f' и f к теоретическим частотам:


 Условия: 1)Количество измерений: n ≥ 30; 2) Теоретическая частота: f ≥ 5
Условия: 1)Количество измерений: n ≥ 30; 2) Теоретическая частота: f ≥ 5
 Коэф-т Фехнера: мера тесноты связи виде отклонения разности числа пар совпадений и несовпадений признаков отклон. от среднего.
Коэф-т Фехнера: мера тесноты связи виде отклонения разности числа пар совпадений и несовпадений признаков отклон. от среднего.





 степень аппроксимации
степень аппроксимации



