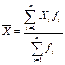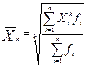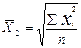Основные этапы статистического анализа.

1.Планирование сбора данных- нужно гарантировать, что сбор данных будет беспристрастным, все объекты имеют шанс быть собранными.

2.Сбор данных

Способы сбора данных: 1.опрос,анкетирование, 2.наблюдение, 3.эксперимент, 4.изучение офиц.источников.

3.Систематизация собранных данных. Первичная оценка данных и оценки неизвестных величин

4.Проверка гипотезы

Закон больших чисел

если эксперимент проведен много раз, относит. частота близка к вер-ти.

Пр:Монету подбросили. Вер-ть падения решкой? Р=1/2=0,5 (50%)

Df: Вер-ть события А=кол-во благопр.исходов/общее кол-во исходов

Вер-ть соб А(с чертой)=1-Вер.соб А

*Формула Байеса: P(A:B) = P(B:A) * P(A) / ((P(B:A) * P(A) +P(B: Ā) * P(Ā))

Статистич сов-ть

сов-ть объектов или явлений одного и того же вида, объединенных наличием общих признаков. Единица стат сов-ти - первич. элемент статистич сов-ти, являющийся носителем признаков, подлежащих исследованию.

Признак -св-во, присущее единице сов-ти.

Стат.показатель -обобщающая хар-ка всей сов-ти

Признаки

конкретное св-во единиц совок-ти, которое можно пронаблюдать и измерить.

1-по стадии исследования (первичный, вторичный)

2-по отношению к исследуемому объекту (прямые -характер св-ва, непосредственно присущие объекту исслед-я; косвенные -хар.св-ва, присущие не самому объекту исследования, а объектам, связанным с объектом исследования)

3-по форме выражения (количестенные (непрерывные - могут приним любое знач, дискретные - могут приним определённые заранее известные значения)

качественные (порядковые; номинальные)

4-по хар-ру взаимосвязи (факторные влияют на рез-т,; результативные)

5-по хар-ру вариации (альтернативные - призн, кот приним 2 значен; с кол-вом вариантов >2-х).

Абсолютные величины - показатель, представляющий собой количеств. хар-ки изучаемых явлений.

Относительные величины -показатели, получаемые сопоставлением абсолютн. или относит. величин.

Виды:ОВ структуры-определ.долю части в общем V сов-ти(часть единиц сов-ти/общий V сов-ти)

§ ОВ координации –соотношение между 2-мя частями исследуемой сов-ти (одна часть сов-ти/др.часть этой же сов-ти, обычно в числит.меньш.число)

§ ОВ выполн.плана (фактич.ур-нь явления/плановый ур-нь явления)

§ ОВ сравнения-соотношение одноименных абсолютных показателей, относящихся к разным объектам, но к одному и тому же времени) (одна сов-ть/др сов-ть) Одноименные!!!

§ ОВ интенсивности-отношение между разноименными абсол.величинами (одна сов-ть/др сов-ть) Разноименные!!! (л.молока/поголовье скота)

Статистическое наблюдение

§ сбор сведений по заранее разработанному плану. Реализуется посредством отчетности-по установл.формам, в установленный срок; посредством спец.организ.обследований).

§ Виды статистического наблюдения

§ 1)По охвату единиц сов-ти (сплошное/несплошное).

§ 2) По времени регистрации (текущее/единовременное/ периодическое).

§ 3)По способу регистрации: корреспондентский, экспедиционный, анкетный, саморегистрация, явочный

§ 4) По источникам получения информации (наблюдение/Документальный способ/Опрос)

§ План статистического наблюдения

§ 1)Программно-методологическая часть: 1. Цель и задачи 2. Объект и единицы 3. Время начала - окончания 4. Программа

§ 2)Организационная часть: 1. Сроки и место 2. Кадровое обеспечение 3. Организация сбора данных 4. Технология обработки 5. Орг.-хоз. мероприятия

§

§ 2. Выборочное наблюдение

§ разновидность наблюдения, охватывает отобранную часть единиц генеральной совокупности. Цель - по отобранной части единиц дать характеристику всей генеральной совокупности.

§ Выб. набл. должно быть репрезентативным. Репрезентативность - каждое св-во и в выборке и в генер.совокупности имеет одинаковые частоты.

§ Способы отбора: 1)Перепись(n=N), 2)Без возврата или с возвратом, 3)Неслучайная или случайная, 4)Стратифицированная (исп-ем естеств.подгруппы-страты)

§

§ 9. Ошибки наблюдения:

§ 1. Репрезентативности- соотношение результатов не совпадает с тем, что есть;

§ 2. Регистрации: преднамеренные -непреднамеренные: а) случайные б) систематические

§ Контроль данных: Логический (может поставить под сомнение правильность полученных данных, поскольку основан на логической взаимосвязи между признаками) и Арифметический (для проверки итоговых сумм).

§ Выбросы. 1. ошибки (некорректно введённые данные), 2. отличающиеся значения (данные не относятся к исследуемому набору/исключительное явление).

 

При исключении выбросов всегда объяснять причину!

 

Группировка

распределение единиц по группам т.о., чтобы различия между единицами отнесенными к одной группе были <, чем различия между единицами отнесенными к разным группам.

Статист. представление инф-ции:

-статистические таблицы

-статист.графики

 

3. Вариация

многообразие значений признака у единиц данной совокупности.

Вариационный ряд - упорядоченное распределение единиц совокупности (ряд распределения).

Показатели вариации - числовые характеристики статистического распределения, демонстрирующие степень рассеяния наблюдаемых значений измеряемого показателя относительно их среднего значения.

Чем выше показатели вариации, тем больший наблюдается разброс в значениях измеряемого показателя, и тем менее надежны результаты измерений. Размах, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэф-т осцилляции, коэф-т вариации.

5 базовых показателей вариационного ряда: min, max,1-й квартиль, медиана, 3-й квартиль.

. Виды вариационных рядов

Ранжированный (если объектов не много)

Ранжирование позволяет легко разделить кол-ые данные по группам, сразу обнаружить наим.и наиб.значения признака, выделить значения, кот.чаще всего повторяются.

 

Дискретный (если объектов много, а признак принимает небольшое число возм-ых значений). Интервальный (если признак может принимать большое количество значений или эти значения могут быть дробными-объединяем значения признака в интервал).

 

Интервальный ряд

если признак может принимать большое количество значений или эти значения могут быть дробными- объединяем значения признака в интервал.

Формула Стерджеса:К=1+3,322lg(n)

i=R/K R=(xmax-xmin) (размах)

K – количество интервалов (групп), n – кол-во единиц совокупности, i – величина интервала.

5 Средняя величина

обобщающая величина изучаемого признака совокупности

1.(Простое)Выборочное среднее = сумма значений элементов данных/количество элементов данных. Для ранжированного ряда

 

для генеральной совокупности- μ

Взвешенное среднее

 

 

Степенные средние.

Виды:

Простые Взвешенные

 

(k-степень ср. величины)

Среднее гармоническое (К = -1):

простое взвешенное

 

Применяем для оценки средних затрат труда, времени, расстояния, материалов

на единицу продукции.

Среднее геометрическое (К=0):

простое взвешенное

 

 

П -произведение

Применяем для интегрального сравнения объектов

Среднее квадратическое (К=2):

простое взвешенное

 

Для исчисления среднего квадратического отклонения.

Среднее кубическое (К=3 ):

простое взвешенное

 

 

Правило мажорантности средних:

(Хгарм<Xгеом<Харифм<Хквадр<Хкуб)

6. Ряды распределения

В зависимости от того, какой признак (количественный или качественный) взят за основу группировки данных, различают:

Атрибутивный ряд распределения - качественный признак

Вариационный - количественныйу признак.

Построить вариационный ряд - значит упорядочить количественное распределение единиц совокупности по значениям признака, а затем подсчитать числа единиц совокупности с этими значениями.

Вариационные ряды:

Ранжированный (если объектов не много)

Дискретный (если признак принимает небольшое число значений). В основу построения положены признаки с прерывными изменениями (дискретные признаки-кол-во детей в семье, число работников на предпр-ии,.Строится табл., где каждая строчка значения признака- кол-во единиц совокупности с данным значением признака.Табл.состоит из 2-х граф. В 1-ой-указ-ся конкретное значение признака, а во 2-ой-число единиц сов-ти с опред.значением признака.

Интервальный (если признак может принимать большое количество значений или эти значения могут быть дробными- объединяем значения признака в интервал). Если признак имеет непрерывное изменение (размер дохода, стаж работы). Групповая таблица имеет 2 графы. В 1-ой указ-ся значение признака в интервале «от-до»(вар-ты), во 2-ой-число единиц, входящих в интервал(частота).

Формула Стерджеса К=1+3,322lg n

i=R/K R=(xmax-xmin)

K – количество интервалов, n – кол-во единиц совокупности, i – величина интервала.

. Характеристики центра распределения

Средняя величина - обобщающая величина изучаемого признака совокупности, характеризующая типичный уровень совокупности.

Мода- величина признака, кот встречается в ряду распределения чаще всего.

Бимодальное распред. -распределение значений признака

Унимодальное -одна ярко выраженная мода

Если ряд ранжированный-переводим его в дискретный. Мода в дискретном ряду считается- считаем частоту по каждому признаку и выбираем наиболее часто встречаемый.

Медиана —значение, расположенное посередине ранжированного вариационного ряда.

Порядковый номер(ранг)= (n+1)/2

Соотношение среднего, моды и медианы:

Хср<Ме<Мо- левосторонняя асимметрия

Мо<Ме<Хср- правосторонняя

Мо=Ме=Хср- классическое нормальное распределении.