
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели центра распределенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Средняя арифметическая взвешенная:
где
В связи с тем, что в Excel отсутствует формула для вычисления средней арифметической взвешенной в ячейку В84 запишем выражение = СУММПРОИЗВ (V3:V7). Мода и медиана относятся к структурным средним. Их значения находятся из выражений:
где
Формулы (15,16 и17) записаны в ячейках B84,В85 и В86 соответственно. В первом пункте задания сделан вывод о правосторонней асимметрии, а по сгруппированным данным получается, что асимметрия левосторонняя, т.к. Противоречие объясняется некоторым произволом в выборе количества групп. Для каждой из 4-х представленных на рис. 5,6, 7, 9 диаграммах будут свои значения
Показатели вариации 1. Размах вариации (формула 15, ячейка В76). 2. Среднее линейное отклонение (ячейка В87):
3. Дисперсия (ячейка В88):
4. Среднее квадратическое отклонение (ячейка В89):
5. Коэффициент осцилляции (ячейка В90):
6. Линейный коэффициент вариации (ячейка В91):
7. Коэффициент вариации (ячейка В92):
8. Относительный показатель квартильной вариации (ячейка В93):
где
В практике из показателей вариации получили широкое применение дисперсия, среднее квадратическое отклонение и коэффициент вариации. Показатели дифференциации 1. Коэффициент фондовой дифференциации
где Формула (26) реализована в ячейке В94. Средние значения активов «богатых» банков превышают средние значения активов «бедных» в 1,5 раза. 2. Коэффициент децильной дифференциации
где
Выражения (27-29) реализованы в ячейке В95. Из двух показателей предпочтение следует отдать коэффициенту фондовой дифференциации. Его значение более устойчиво (при соблюдении правил округления) по сравнению с коэффициентом децильной дифференциации, зависящего от количества групп в структурной группировке. Кроме того, оба показателя являются ненормированными. Вследствие этого одно и тоже значение каждого из них можно толковать по-разному. Для устранения указанной неопределенности условимся вычислять значения
Оценку степени дифференциации можно осуществить по шкале Чеддока:
Учитывая, что расчетное значение
Показатели концентрации 1. Кривая Лоренца В статистике для изучения степени неравномерности распределения определенного суммарного показателя между единицами отдельных групп вариационного ряда используется кривая Лоренца (или кривая концентрации). Для ее построения распределение единиц совокупности (числа банков) и распределение суммарного показателя (суммы активов в банках) должны быть представлены в долях или процентах, а затем для обоих распределений рассчитываются накопленные (кумулятивные) итоги. В данном примере суммы активов в j-ой группе банков приведены в ячейках Z2: Z7, которые рассчитаны с помощью функции СУММ. Их соответствующие частости помещены в ячейки АА2: АА7. Кумулятивные итоги в частостях размещены в ячейках Y2: Y7 и АВ2: АВ7, а в процентах – AD2: AD7, AE2: AE7. Кривая Лоренца приведена на рис.7. Она построена с помощью мастера диаграмм, тип «точечная». Диалоговое окно приведено на рис. 8. Рисунок 7
Рисунок 8
2. Коэффициент Джини Рассчитывается на основе кривой Лоренца
где Формула (30) реализована в ячейке В96. Учитывая, что коэффициент Джинни равен 0,09, концентрация активов банков практически отсутствует.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 634; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.006 с.) |

 , (16)
, (16)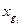 - значения j-ой середины интервалов;
- значения j-ой середины интервалов;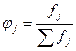 - частости j-го интервала.
- частости j-го интервала. (17)
(17) (18)
(18) - нижние границы модального и медианного интервалов;
- нижние границы модального и медианного интервалов; - ширина модального и медианного интервалов;
- ширина модального и медианного интервалов; - частость модального интервала;
- частость модального интервала; - частость интервала, предшествующему модальному;
- частость интервала, предшествующему модальному;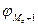 - частость интервала следующего за модальным;
- частость интервала следующего за модальным;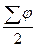 - половина суммы накопленных частостей (равна 0,5);
- половина суммы накопленных частостей (равна 0,5); - накопленная частость до медианного интервала;
- накопленная частость до медианного интервала; - частость медианного интервала.
- частость медианного интервала.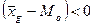 .
. , отличающиеся друг от друга. Если существует возможность вычислить значения
, отличающиеся друг от друга. Если существует возможность вычислить значения 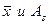 по несгруппированным данным, то ее необходимо использовать.
по несгруппированным данным, то ее необходимо использовать. . (19)
. (19) . (20)
. (20)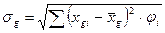 . (21)
. (21) . (22)
. (22)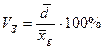 . (23)
. (23) . (24)
. (24) , (25)
, (25)
 ;
;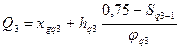 ;
;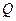 - квартильное отклонение;
- квартильное отклонение; - соответственно первая и третья квартили распределения;
- соответственно первая и третья квартили распределения;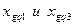 - нижние границы интервалов, в которых находятся первая и третья квартили;
- нижние границы интервалов, в которых находятся первая и третья квартили; - ширины интервалов первой и третьей квартили;
- ширины интервалов первой и третьей квартили; и
и 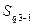 - сумма накопленных частостей в интервалах предшествующих интервалам, в которых находятся первая и третья квартили;
- сумма накопленных частостей в интервалах предшествующих интервалам, в которых находятся первая и третья квартили;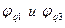 - частости интервалов, в которых находятся первая и третья квартиль.
- частости интервалов, в которых находятся первая и третья квартиль. , (26)
, (26) - средние значения для 10% банков с наибольшими и для 10% с наименьшими значениями активов.
- средние значения для 10% банков с наибольшими и для 10% с наименьшими значениями активов. , (27)
, (27) - максимальное значение активов у 10% банков с наименьшими активами;
- максимальное значение активов у 10% банков с наименьшими активами; - минимальное значение активов у 10% банков с наибольшими активами;
- минимальное значение активов у 10% банков с наибольшими активами; ; (28)
; (28) ; (29)
; (29)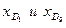 - нижние границы интервалов, в которых находятся первая и девятая децили;
- нижние границы интервалов, в которых находятся первая и девятая децили; - ширины интервалов первой и девятой децили;
- ширины интервалов первой и девятой децили; - сумма накопленных частостей в интервалах, предшествующих интервалам, в которых находятся первая и девятая децили;
- сумма накопленных частостей в интервалах, предшествующих интервалам, в которых находятся первая и девятая децили; - частости интервалов, в которых находятся первая и девятая децили.
- частости интервалов, в которых находятся первая и девятая децили. и
и  по формулам:
по формулам: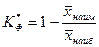


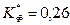 , степень дифференциации банков по стоимости активов является слабой.
, степень дифференциации банков по стоимости активов является слабой.

 , (30)
, (30)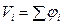 ,
,  .
.


