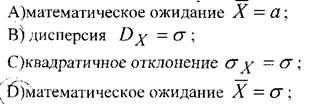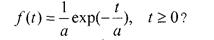Какими показателями измеряется разброс наработки на отказ.

В)Дисперсией;

С)Квадратичным отклонением

D)Коэффициентом вариации

10.3а время наблюдения за работой станка получено, что суммарное времяработы было равно t_p, а суммарное время восстановления отказов станка оказалось равным t_B. Как оценить удельное время восстановления?

11.3a время наблюдения за работой станка получено, что суммарное время работы было равно t_p, а суммарное время восстановления отказов станка оказалось равным t_в. Как оценить коэффициент готовности?

12.3а время наблюдения за работой станка получено, что суммарное время работы было равно t_p, суммарное время восстановления отказов станка оказалось равным t_B, суммарное время организационных простоев равно t_op. Как оценить коэффициент технического использования?

13.Укажите ошибочные утверждения. Станок может находиться в нескольких состояниях i -1,..., N с вероятностями P₁ ,..,P_N, q₁,..,q_N - производительности станка в отмеченных состояниях.

14.Укажите ошибочные утверждения. Станок может находиться в нескольких состояниях i - 1,...,N с вероятностями P₁,...,P_N, q₁,..,q_N - производительности станка в отмеченных состояниях.

15.Станок может находиться в нескольких состояниях i= 1,...,N с вероятностями P₁,...,P_N, q₁,..,q_N - производительности станка в отмеченных состояниях. Что верно?

А)Номинальная производительность станка

16.Станок может находиться в нескольких состояниях 1 = 1,..., N с вероятностями P₁,...,P_N, q₁,..,q_N - производительности станка в отмеченных состояниях. Что верно?.

А)Средняя производительность станка

РАЗДЕЛ 6 Распределения.

Какие законы распределения целесообразно применять для характеристики надежности режущего инструмента.

В)3акон Вейбулла-Гнедеико.

Плотность какого распределения называется нормальной?

Плотность какого распределения называется показательной?

Плотность какого распределения имеет закон Вейбулла?

Плотность какого распределения называется гамма распределением?

Какими свойствами обладает показательное распределение? Укажите ошибочное утверждение.

D)Опасность отказов пропорциональна наработке объекта.

Какими свойствами обладает распределение Вейбулла? Укажите ошибочное утверждение.

С)Опасность отказов не зависит от наработки объекта.

Какими свойствами обладает нормальное распределение? Укажите ошибочное утверждение..

В)Накопленные величины случайных процессов имеют в пределе нормальное распределение

9.Какую плотность распределения имеет неслучайная величина Х=а?

B) -Дельта функция Дирака.

Какие характеристики имеет неслучайная величина Х-а? Укажите ошибочное утверждение.

B)Диcперcия равна 1;

11.Правильно ли, что неслучайная величина X = а имеет функцию распределения F(x) равную О-при х < а и 1 при х > а?

A) Да;

12.Укажите ошибочное утверждение. Если X — а неслучайная величина то:

B)дисперсия Dx = 1;

13.Что верно? Если X = а неслучайная величина с плотностью распределения f(x) = S(x - а), то:

А)математическое ожидание X = а;

Нормально распределенная величина X имеет плотность распределения

Что верно?

Нормально распределенная величина X имеет плотность распределения

. Что ошибочно?

РАЗДЕЛ 7 Распределения 2.

Какими свойствами обладает нормальное распределение?

А)Сумма независимых случайных величин с ростом числа слагаемых стремится к нормальному

распределению;

С)Нормальное распределение обладает свойством безграничной делимости;

Когда на практике целесообразно применять нормальное распределение?

А)Как распределение накапливающихся случайных величин;

З.Как выражается плотность случайной величины X с показательнымраспределением?

4.Как выражается функция надежности объекта с показательным распределением наработки на отказ Т, если средняя наработка на отказ

5.Чему равно математическое ожидание случайной величины Т с плотностью распределения

Чему равна дисперсия случайной величины Т с плотностью распределения