
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Какое восстановление называется профилактическим?Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте С)Восстановление называется профилактическим, если оно проводится после наступления частичного отказа объекта. D)Восстановление называется профилактическим, если оно проводится после выработки объектом планового ресурса. 12.
13.
14.В1,..., Вп- удельные времена восстановления структурных единиц системы простой структуры. Как определяется удельное время восстановления системы при последовательном восстановлении?
15.В1,...,Вп- удельные времена восстановления структурных единиц системы простой структуры. Как определяется коэффициент готовности системы при последовательном восстановлении?
16. P1 (t),…, Рп(t)- функции надежности структурных единиц системы простой структуры. Как определится функция надежности системы простой структуры при параллельном восстановлении?
17. P1 (t),…, Рп(t)- функции надежности структурных единиц системы простой структуры. Как определится средняя наработка на отказ системы при параллельном восстановлении?
18.
19.Инструменты наладки из N одинаковых инструментов имеют функцию надежности
20.Инструменты наладки из N=16 одинаковых инструментов имеют функцию надежности
21.Инструменты наладки из N=16 одинаковых инструментов имеют функцию надежности
22.Инструменты наладки из N=16 одинаковых инструментов имеют функцию надежности
23.Наладка состоит из N одинаковых инструментов, восстанавливаемых параллельно, T1 -средняя стойкость одного инструмента. При каком значении коэффициента вариации стойкости инструмента Ку стойкость наладки Т = Т1? C)Кv=0 Зависит ли средняя стойкость наладки с несколькими инструментами при последовательном восстановлении от коэффициентов вариации стойкости отдельных инструментов? А)3ависит; Зависит ли средняя стойкость наладки с несколькими инструментами при параллельном восстановлении от коэффициентов вариации стойкости отдельных инструментов? В)Не зависит; РАЗДЕЛ 12 Профилактика 1.Укажите ошибочное утверждение; С)Профилактическое восстановление хуже восстановления по отказу, если коэффициент вариации наработки на отказ объекта больше или равен единице. D)Профилактическое восстановление хуже восстановления по отказу, если опасность отказов объекта имеет стареющий тип. Какие преимущества и недостатки имеет система профилактики с жестким графиком? Укажите ошибочное утверждение. В)Профилактика с жестким графиком более экономична по сравнению с другими вариантами организации; С)Профилактика с жестким графиком имеет смысл только при возрастающей опасности отказов. 3.Можно ли применять профилактическое восстановление для объекта спадающей опасностью отказов и почему? B)не выгодно.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 534; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 - интенсивности отказов структурных единиц системы простой структуры. Как определяется общая интенсивность отказов системы при последовательном восстановлении?
- интенсивности отказов структурных единиц системы простой структуры. Как определяется общая интенсивность отказов системы при последовательном восстановлении?


 (подойти сказать В, а не Кг)
(подойти сказать В, а не Кг)

 - функции надежности структурных единиц системы простой структуры. Как определится средняя наработка на отказ системы Т при параллельном восстановлении, если Тi - собственные средние наработки на отказ структурных единиц, 1,…, N?
- функции надежности структурных единиц системы простой структуры. Как определится средняя наработка на отказ системы Т при параллельном восстановлении, если Тi - собственные средние наработки на отказ структурных единиц, 1,…, N?
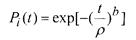 (закон Вейбулла). Чему будет равна средняя стойкость наладки при параллельном восстановлении, если Тi- средняя стойкость одного инструмента?
(закон Вейбулла). Чему будет равна средняя стойкость наладки при параллельном восстановлении, если Тi- средняя стойкость одного инструмента?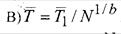
 (закон Вейбулла) с параметром b=2. Чему будет равна средняя стойкость наладки при параллельном восстановлении, если Ti- средняя стойкость одного инструмента?
(закон Вейбулла) с параметром b=2. Чему будет равна средняя стойкость наладки при параллельном восстановлении, если Ti- средняя стойкость одного инструмента?
 (закон Вейбулла) с параметром b=2. Чему будет равна средняя стойкость наладки при последовательном восстановлении, если Т\ - средняя стойкость одного инструмента?
(закон Вейбулла) с параметром b=2. Чему будет равна средняя стойкость наладки при последовательном восстановлении, если Т\ - средняя стойкость одного инструмента?
 (закон Вейбулла) с параметром b=2. Чему будет равна средняя стойкость наладки при параллельно-последовательном восстановлении, если Ti- средняя стойкость одного инструмента, которые разбиты на 4 группы с параллельным восстановлением по 4 инструмента в группе?
(закон Вейбулла) с параметром b=2. Чему будет равна средняя стойкость наладки при параллельно-последовательном восстановлении, если Ti- средняя стойкость одного инструмента, которые разбиты на 4 группы с параллельным восстановлением по 4 инструмента в группе?



