
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка правила сложения дисперсий и оценка степени влияния факторного признака на величину результативного.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Правило сложения дисперсий заключается в равенстве общей дисперсии сумме средней из внутригрупповых и межгрупповой дисперсий, т.е.:
где
Значение общей средней приведено в ячейке D65, а в ячейках D66 и D67 – среднее квадратическое отклонение и дисперсия зависимой переменной. Групповые средние приведены в ячейках АУ3:АУ7. Внутригрупповые дисперсии вычисляются с использованием функции ДИСПР, например, в ячейке АК3 записана формула = ДИСПР (С10:С15). Средняя из внутригрупповых дисперсий отображена в ячейке D68, в которой записана формула: = СУММПРОИЗВ (АК3:АК7;Х3:Х7). Для вычисления межгрупповой дисперсии в ячейку D69 записана формула = СУММПРОИЗВ (СТЕПЕНЬ(AJ3:АJ7-$D$65;2);X3:X7). Как следует из данных табл. 2 правило сложения дисперсий выполняется, т.к. 11,25=1,62+9,63. Для того, чтобы выяснить влияет ли контролируемый фактор на результативный признак, а при наличии такого влияния оценить его степень можно применить однофакторный дисперсионный анализ. Его логика рассуждений сводится к следующему: Пусть В связи с тем, что числовые значения математических ожиданий неизвестны, то возникает задача проверки гипотезы
Проверить данную гипотезу можно при соблюдении следующих требований при каждом значении уровня фактора: 1) наблюдения независимы и проводятся в одинаковых условиях; 2) результативный признак имеет нормальный закон распределения с постоянной для различных уровней генеральной дисперсией. Для ответа на второй вопрос вычислим значения относительных показателей асимметрии и эксцесса (ячейки В71, В72). Учитывая, что каждый из них меньше 1,5 эмпирическое распределение прибыли банков не противоречит нормальному. Проверим выполнение гипотезы:
с помощью критерия Бартлетта:
где l=n-m;
k=m-1; (55)
При выполнении гипотезы о равенстве дисперсий, величина w имеет распределение близкое к При соблюдении условия
Здесь Проверка гипотезы о равенстве математических ожиданий основывается на сравнении оценок
имеет F – распределения с числом свободы k=m-1 и
При использовании F – критерия строится правосторонняя область ( Рассчитаем значение перечисленных показателей. В ячейке D72 записана формула = n-m, т.е. вычисляется значение Ячейка D73 содержит формулу =СУММПРОИЗВ(СТЕПЕНЬ(W3:W7-1;(-1))) – вычисляется значение Ячейка D74: =1/D72 – вычисляется значение Ячейка D75: =СУММПРОИЗВ(W3:W7-1;AK3:AK7)*D74 – вычисляется значение Ячейка D76: =1+(D73-D74)/(3*4) – вычисляется значение q; Ячейка D77: =СУММПРОИЗВ(W3:W7-1;LN($D$75/AK3:AK7))/D76 – вычисляется значение критерия Бартлетта; Ячейка D78: =ХИ20БР(0,05;4) – определяется значение правосторонней критической точки В связи с тем, что
Обратимся к режиму работы «Однофакторный дисперсионный анализ». Значения параметров, установленные в одноименном диалоговом окне, показаны на рис. 15.
Рисунок 15
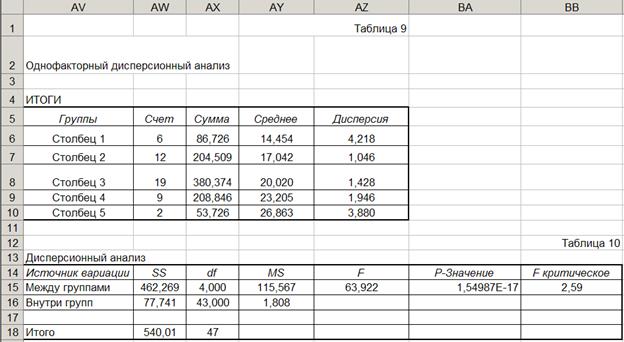
Показатели, рассчитанные в ходе проверки гипотезы приведены в табл. 9 и 10.
Как видно из табл. 10 расчетное значение F – критерия Рассмотрим более подробно алгоритм расчета основных показателей, представленных в табл. 10. В ячейке AW15 (показатель SS между группами) рассчитывается взвешенная сумма квадратов отклонений групповых средних от общей выборочной средней:
В ячейке AW16 (показатель SS внутри групп) вычисляется остаточная сумма квадратов отклонений наблюдаемых значений уровня от своей выборочной средней:
В ячейке AW18 (показатель SS итого) общая сумма квадратов отклонений наблюдаемых значений от общей выборочной средней: В ячейках АХ15, АХ16 и АХ17 (показатель df) определяются степени свободы:
В ячейках AY15:AY16 (показатель MS) вычисляются несмещенные оценки
В ячейке AZ15 (показатель F) вычисляется расчетное значение критерия
В ячейке ВА15 (показатель Р – значение) определяется Р – значение, соответствующее расчетному значению критерия =FРАСП(AZ15;AX15;AX16) В ячейке ВВ15 (показатель F критическое) рассчитывается значение правосторонней критической точки =FРАСПОБР(0,05;АХ15;АХ16). Разделив левую и правую части выражения (42) на общую дисперсию получим следующее равенство:
Т.е. доли средней из внутригрупповых и межгрупповой дисперсий в сумме равны единице. Второе слагаемое именуется эмпирическим коэффициентом детерминации
Он характеризует долю объясненной дисперсии в общей. Следовательно 86% (ячейка D70) вариации прибыли банков объясняются величиной их активов. Для оценки тесноты зависимости используется эмпирическое корреляционное отношение
Учитывая, что При недостаточном количестве данных в выделенных группах к рассчитанной величине корреляционного отношения водится поправка на группировку:
откуда Таким образом можно сделать вывод, что эмпирический коэффициент детерминации является значимым и его можно применять для оценки влияния суммы активов банков на величину их прибыли.
Оценка степени взаимной согласованности между суммой активов банков и величиной их прибыли с помощью линейного коэффициента корреляции. Проверка его значимости и возможности использования линейной функции в качестве формы уравнения. Линейный коэффициент корреляции в EXCEL можно вычислить используя режим «Корреляция» только для несгруппированных данных. Поэтому в ячейке D83 записана формула =(СУММПРОИЗВ(V3:V7:AY3:FY7;X3:X7)-B84*D65)/(B89*D66) или в принятых обозначениях Значение коэффициента детерминации (
Рисунок 16
Из приведенных результатов следует, что степень взаимной согласованности между суммой активов банков и величиной их прибыли весьма высокая. В связи с тем, что линейный коэффициент корреляции определен по выборочным данным, то его значение может существенно отличаться от аналогичного показателя в генеральной совокупности. Поэтому необходимо определить значимость выборочного линейного коэффициента корреляции. При наличии значимости определяются границы доверительного интервала линейного коэффициента корреляции и его можно использовать для оценки степени тесноты связи. Оценку значимости линейного коэффициента корреляции выполним на основе t – критерия Стьюдента
где При этом проверяется гипотеза Так как рассчитанное значение При недостаточном объеме выборки для построения доверительного интервала коэффициент корреляции преобразуют в величину
Данное выражение имеет название «z – преобразование Фишера». Интервальная оценка для z определяется из выражения
где Приведем реализацию изложенного алгоритма. · ячейке D91 содержится формула =ФИШЕР(D83) – вычисляется значение · в ячейках D92 и D93 содержатся формулы =D91-НОРМСТОБР((0,95+1)/2)*КОРЕНЬ(1/45) и =D91+ НОРМСТОБР((0,95+1)/2)*КОРЕНЬ(1/45) – рассчитываются интервальные оценки z; · ячейки D94 и D95 содержатся формулы =ФИШЕРОБР(D92) и ФИШЕРОБР(D93). Таким образом, с вероятностью 0,95 линейный коэффициент корреляции заключен в интервале от 0,87 до 0,96 со стандартной ошибкой 0,06. Проверка возможности использования линейной функции в качестве формы уравнения заключается в определении разности квадратов
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 587; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.42.59 (0.01 с.) |

 , (42)
, (42)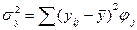 общая дисперсия; (43)
общая дисперсия; (43)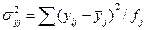 внутригрупповые дисперсии; (44)
внутригрупповые дисперсии; (44)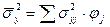 средняя из внутригрупповых дисперсий; (45)
средняя из внутригрупповых дисперсий; (45)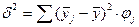 межгрупповая дисперсия; (46)
межгрупповая дисперсия; (46) внутригрупповые средние; (47)
внутригрупповые средние; (47)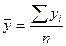 общая средняя. (48)
общая средняя. (48) - математическое ожидание результативного признака, соответственно в группах
- математическое ожидание результативного признака, соответственно в группах 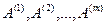 . Если при изменении уровня фактора групповые математические ожидания не изменяются, то результативный признак не зависит от фактора А, в противном случае такая зависимость имеется.
. Если при изменении уровня фактора групповые математические ожидания не изменяются, то результативный признак не зависит от фактора А, в противном случае такая зависимость имеется.
 (49)
(49) (50)
(50) ; (51)
; (51) ; (52)
; (52) ; (53)
; (53)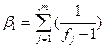 ; (54)
; (54) - дисперсия в j-ой группе.
- дисперсия в j-ой группе. с к=m-
с к=m-  степенями свободы.
степенями свободы. гипотеза (49) подтверждается. (56)
гипотеза (49) подтверждается. (56)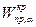 - правосторонняя критическая точка при заданном уровне значимости
- правосторонняя критическая точка при заданном уровне значимости  , определяющая критический интервал (
, определяющая критический интервал (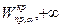 ).
). и
и  . В математической статистике доказывается, что если гипотеза о равенстве математических ожиданий подтверждается, то величина
. В математической статистике доказывается, что если гипотеза о равенстве математических ожиданий подтверждается, то величина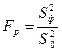 (57)
(57)
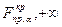 ), т.к. обычно
), т.к. обычно  . Если расчетное значение F – критерия
. Если расчетное значение F – критерия  попадает в указанный интервал, то гипотеза о равенстве групповых математических ожиданий отвергается, т.е. считаем, что фактор А влияет на результативный признак Y и можно измерить степень этого влияния с помощью выборочного коэффициента детерминации.
попадает в указанный интервал, то гипотеза о равенстве групповых математических ожиданий отвергается, т.е. считаем, что фактор А влияет на результативный признак Y и можно измерить степень этого влияния с помощью выборочного коэффициента детерминации. ;
; ;
;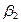 ;
;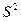 ;
; =3,18 не попадает в критическую область (9,49;
=3,18 не попадает в критическую область (9,49;  ), то гипотеза
), то гипотеза 

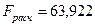 , а критическая область образуется правосторонним интервалом (2,59:
, а критическая область образуется правосторонним интервалом (2,59:  .
. .
. или
или 
 ;
; ;
;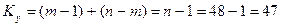 .
. и
и 


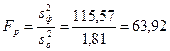 .
. с помощью формулы:
с помощью формулы: . (58)
. (58) . (59)
. (59)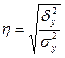 . (60)
. (60) (ячейка D71) теснота зависимости (по шкале Чеддока) весьма высокая.
(ячейка D71) теснота зависимости (по шкале Чеддока) весьма высокая. , (61)
, (61) (ячейки D81 и D82).
(ячейки D81 и D82). . (61)
. (61) ) приведено в ячейке D84. Для сравнения в ячейке D86 и D87 приведены значения перечисленных показателей для несгруппированных данных, вычисленные с использованием функции ПИРСОН (В10: В57; С10:С57), диалоговое окно которого приведено на рис. 16.
) приведено в ячейке D84. Для сравнения в ячейке D86 и D87 приведены значения перечисленных показателей для несгруппированных данных, вычисленные с использованием функции ПИРСОН (В10: В57; С10:С57), диалоговое окно которого приведено на рис. 16.
 , (62)
, (62) - стандартная ошибка линейного коэффициента корреляции (ячейка D96) (63)
- стандартная ошибка линейного коэффициента корреляции (ячейка D96) (63) о равенстве нулю коэффициента корреляции (
о равенстве нулю коэффициента корреляции (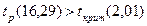 , гипотеза
, гипотеза  , имеющую приблизительно нормальное распределение и рассчитываемую по формуле
, имеющую приблизительно нормальное распределение и рассчитываемую по формуле (64)
(64) (65)
(65) - табулированые значения для стандартного нормального распределения, зависимые от
- табулированые значения для стандартного нормального распределения, зависимые от 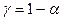 . На основе обратного
. На основе обратного 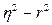 , если она меньше 0,1, то считается возможным использовать линейное уравнение корреляционной зависимости. В данном случае эта разность составляет 0,004 (ячейка D85).
, если она меньше 0,1, то считается возможным использовать линейное уравнение корреляционной зависимости. В данном случае эта разность составляет 0,004 (ячейка D85).


