
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение уравнения парной регрессииСодержание книги
Поиск на нашем сайте
При линейной связи параметры уравнения парной регрессии:
находится из системы уравнений:
которая получается применением метода наименьших квадратов. Из первого уравнения системы следует, что:
Подставив полученное выражение во второе уравнение, получим:
Коэффициент корреляции определяется по формуле:
Учитывая (69) и (70)
или Зная значения r,
Статистический анализ модели Оценка параметров парной регрессии выполняется исходя из следующих предпосылок [8]. Допустим, что в генеральной совокупности связь между x и y линейна. Наличие случайных отклонений, вызванных воздействием на переменную y множества других, неучтенных в уравнении факторов и ошибок измерения, приведет к тому, что связь наблюдаемых величин
Здесь
Для того, чтобы оценки 1. математическое ожидание 2. величина 3. значения 4. дисперсия 5. Остатки распределены по нормальному закону (свойство используется для проверки статистической значимости и построения доверительных интервалов при прогнозировании) Известно, что если данные условия выполняются, то оценки, сделанные с помощью метода наименьших квадратов, обладают следующими свойствами: 1. оценки являются несмещенными, т.е. математическое ожидание оценки каждого параметра равно его истинному значению:
Это вытекает из того, что
2. оценки состоятельны, т.к. дисперсии оценок параметров при возрастании числа наблюдений стремятся к нулю: 3. оценки эффективны, т.е. они имеют наименьшую дисперсию по сравнению с любыми другими оценками данного параметра. Если предположения 3 и 4 нарушены, т.е. дисперсия возмущений непостоянна или значения Отметим, что аппроксимировать уравнением парной регрессии у на х, имеет смысл только в том случае, если существует достаточно тесная статистическая зависимость между случайными величинами и линейный коэффициент корреляции является значимым, что и имеет место в рассматриваемом примере.
Оценка качества построенной модели Близость точек исходных данных и линий регрессии на графике корреляционного поля (рис. 17) позволяет судить о качестве модели, но более строгий подход, кроме визуальной оценки, предполагает использование и других критериев. Рисунок 17
Выбор функции для моделирования взаимосвязи между факторами осуществляется на основе формального и неформального подходов. Формальный подход позволяет определить соответствие модели исходному объекту (адекватность) и степень близости ее к фактическим данным (точность). Неформальный подход заключается в логическом исследовании соответствия математической функции, принятой в качестве модели, исследуемой зависимости. При выборе модели можно сначала на основе содержательного анализа исключить заведомо неподходящие функции, а затем выбрать лучшую из оставшихся моделей и по ней осуществлять моделирование. Можно подойти к выбору модели иначе: сначала оценить параметры всех моделей и выбрать лучшую из них по формальным признакам, а затем решать вопрос о ее соответствии исследуемой зависимости в содержательном плане. Формально качество модели определяется ее адекватностью и точностью. Эти свойства исследуются на основе анализа ряда остатков (отклонений расчетных значений от фактических):
При этом адекватность является более важной составляющей качества, но сначала рассмотрим характеристики точности и нормальности ряда остатков, так как некоторые из них используются при расчете различных критериев адекватности.
Характеристики точности Под точностью понимается величина случайных ошибок. Сравнительный анализ точности имеет смысл только для адекватных моделей: среди них лучшей признается модель с меньшими значениями характеристик точности, к которым относятся: - максимальная ошибка - средняя абсолютная ошибка
показывает, насколько в среднем отклоняются фактические значения от модели; - остаточная дисперсия
- средняя квадратическая ошибка
Средняя квадратическая ошибка является наиболее часто используемой характеристикой точности (что объясняется ее связью с остаточной дисперсией, которая играет центральную роль в регрессионном анализе). Значение средней квадратической ошибки всегда несколько больше значения средней абсолютной ошибки, но они имеют схожий смысл – характеризуют среднюю удаленность расчетных значений модели от фактических исходных данных. Обычно точность модели признается удовлетворительной если выполняется условие:
К характеристикам точности можно отнести также множественный коэффициент детерминации
характеризующий долю дисперсии зависимой переменной, объясненный с помощью регрессии, и множественный коэффициент корреляции (индекс корреляции):
В случае парной линейной регрессии значение множественного коэффициента корреляции совпадает с линейным коэффициентом корреляции. Проверка нормальности ряда остатков может быть выполнена приближенно по условиям (6) (ячейки D106 и D107). В связи с тем, что каждый из относительных показателей формы распределения меньше 1,5 эмпирическое распределение ряда остатков не противоречит нормальному.
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 373; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.57.54 (0.01 с.) |

 (66)
(66) , (67)
, (67) . (68)
. (68)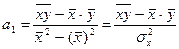 . (69)
. (69)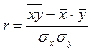 (70)
(70) (71)
(71) (72)
(72)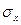 и
и 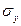 можно вычислить по выражениям (72) и (68) параметры
можно вычислить по выражениям (72) и (68) параметры  и
и 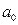 линейного уравнения регрессии.
линейного уравнения регрессии. и
и 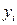 приобретает вид:
приобретает вид: (73)
(73) - случайные ошибки (отклонения, возмущения). Если были бы известны точные значения отклонений
- случайные ошибки (отклонения, возмущения). Если были бы известны точные значения отклонений  и
и  . Так как они неизвестны, то по наблюдениям
. Так как они неизвестны, то по наблюдениям  (74)
(74)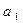 обладали адекватностью ряд остатков
обладали адекватностью ряд остатков  должен удовлетворять следующим требованиям:
должен удовлетворять следующим требованиям: для всех i, j;
для всех i, j;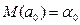
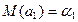
 и свидетельствует об отсутствии систематической ошибки в определении положения линии регрессии;
и свидетельствует об отсутствии систематической ошибки в определении положения линии регрессии; ;
; 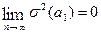 , т.е. надежность оценки при увеличении выборки растет;
, т.е. надежность оценки при увеличении выборки растет;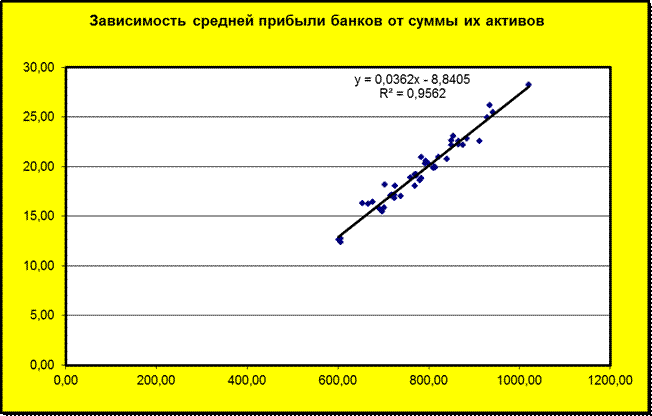
 (75)
(75) соответствует максимальному значению расчетных значений от физических;
соответствует максимальному значению расчетных значений от физических;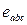
 (76)
(76) ; (77)
; (77)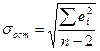 . (78)
. (78) . (79)
. (79) , (80)
, (80) . (81)
. (81)


