
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частные дисперсии и относительные частные дисперсииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Как следует из вышеизложенного в параграфах 3.1 и 4.2, точная форма кривой дисперсии показателя преломления достаточно сложна. Кроме того, эта форма для каждого конкретного оптического материала определяется параметрами свойственного только ему набора осцилляторов и поэтому в какой-то степени варьирует от одного оптического материала к другому (и тем более – от одного типа стекол к другому). Следовательно, такие сложные кривые не могут быть детально охарактеризованы с помощью всего лишь трех точек nl 1, nl 2и nl 3, используемых для рассмотренных выше основных оптических характеристик – главного показателя преломления nl 1, средней дисперсии nl 2- nl 3и коэффициента дисперсии nl 1. В частности, возможны ситуации, когда значения этих оптических характеристик двух материалов практически совпадают, а значения показателя преломления при других длинах волн различаются в достаточной степени. Поэтому наряду с основными оптическими характеристиками в практике применения оптических материалов существенную роль играют и другие оптические характеристики – так называемые частные дисперсии и относительные частные дисперсии. Они служат для детализации изменений показателя преломления материала с длиной волны.
а:
б:
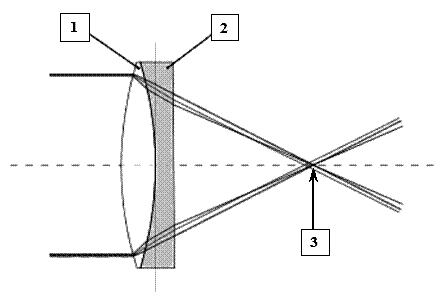
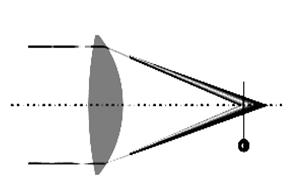
Рис. 31. Двухлинзовый объектив с исправленными хроматическими аберрациями для длин волн синего и красного лучей (простой ахромат). а. Ход синего, зеленого и красного лучей. 1 - положительная (собирающая) линза из материала типа крон, 2 - отрицательная (рассеивающая) линза из материала типа флинт, 3 - положения совмещенной точки фокусов для синего и красного лучей. б. Вторичный спектр (остаточный цветной кружок меньшего диаметра, не содержащий синего и красного лучей) на экране, помещенном в фокальную плоскость желтого луча. Частные дисперсии – это разности nl 4- nl 5двух значений показателя преломления при некоторых произвольно выбранных длинах волн l 4 и l 5, не совпадающих с l 2 и l 3 (как правило, ширина спектральных интервалов l 4 - l 5 существенно меньше, чем ширина интервала l 2 и l 3). Относительные частные дисперсии Pl 4 l 5– это отношения частных дисперсий к средней дисперсии:
Значения частных и/или относительных частных дисперсий также учитываются и при выборе материалов для совершенных оптических систем, и при их расчете. Наиболее важную роль для практики играют частная дисперсия для синего участка спектра ng – nF или ng – nF¢ (здесь ng - показатель преломления для фиолетовой g -линии ртути) и соответствующая ей относительная частная дисперсия PgF (или Pg F¢), поскольку в пределах именно этого участка показатель преломления материала изменяется с длиной волны наиболее значительно. 7.5. Правило Аббе. Нормальная прямая и "особые" стекла. Для наглядного представления специфики относительных частных дисперсий различных оптических материалов Эрнстом Аббе была предложена диаграмма «относительная частная дисперсия – коэффициент дисперсии». Эту диаграмму не принято называть именем автора, чтобы отличать ее от описанной выше диаграммы Аббе. Для участка lg - lF пример диаграммы PgF - nd из современного каталога оптических стекол фирмы Шотт представлен на рис. 32. Эрнстом Аббе было показано, что точки оптических стекол на любой диаграмме Pl 4 l 5- nl 1в основном группируются вокруг некоторой прямой, получившей название «нормальной прямой». Такая нормальная прямая для диаграммы PgF - nd представлена на рис. 32. Тенденцию группировки точек оптических материалов вокруг нормальных прямых на диаграммах Pl 4 l 5- nl 1принято называть правилом Аббе. Оптические материалы, достаточно хорошо подчиняющиеся правилу Аббе (а именно те, точки которых отклоняются от нормальных прямых на величину ÷D nl 1÷ £ 3.0), принято называть «нормальными». Сравнительно немногочисленные оптические материалы, точки которых отклоняются от нормальных прямых на величину ÷D nl 1÷ > 3.0, принято называть «особыми» (в зарубежных каталогах – ”abnormal”).
Рис. 32. Диаграмма PgF - nd из современного каталога оптических стекол фирмы Шотт. Используя символы относительных частных дисперсий, значение упоминавшегося в предыдущем параграфе вторичного спектра D s тонкого двухлинзового объектива можно оценить по формуле
где f ¢ - фокусное расстояние объектива, а индексы 1 и 2 относятся к относительным частным дисперсиям и коэффициентам дисперсии оптических материалов первой и второй линз. Отношение Какие же оптические материалы являются «нормальными», какие - «особыми», и какими физическими, химическими или иными причинами обусловливается попадание материала в число «нормальных» или «особых»? Достаточно давно были разработаны два типа «особых» оптических стекол, объединяемые собирательными терминами «лангкроны» (кроны с увеличенными относительными частными дисперсиями) и «курцфлинты» (флинты с уменьшенными относительными частными дисперсиями). Приставки «ланг-» и «курц-» происходят от немецких слов, обозначающих «длинный» и «короткий» соответственно. До сравнительно недавнего времени в каталоге фирмы Шотт сохранялись некоторые «особые» кроны и флинты с соответствующими обозначениями их типов – LgK, LgSK, KzF, KzFS. В российском каталоге «особые» кроны и флинты обозначались символами ОК и ОФ соответственно. В дальнейшем оказалось, что «особые» свойства являются неотъемлемой чертой оптических стекол некоторых новых типов. В частности, все стекла каталога фирмы Шотт типов LaK, LaF и LaSF и российские стекла типов СТК и ТБФ с достаточно высоким содержанием окиси лантана являются курцфлинтами. Как видно из рис. 32, точки стекол, отклоняющихся от нормальной прямой в сторону более высоких значений относительной частной дисперсии (лангкронов), располагаются в области очень высоких значений коэффициента дисперсии, а стекол, отклоняющихся от нормальной прямой в сторону более низких значений относительной частной дисперсии (курцфлинтов) - в области средних значений коэффициента дисперсии. Кроме них, имеются также немногочисленные стекла, отклоняющиеся от нормальной прямой в сторону более высоких значений относительной частной дисперсии (лангфлинты) и при этом лежащие в области очень низких значений коэффициента дисперсии. Среди «особых» стекол самый большой интерес для конструкторов оптических систем представляют «особые» кроны (лангкроны) с наиболее высокими значениями коэффициента дисперсии и, тем более, оптические кристаллы ряда фторидов (NaF, CaF2, SrF2и BaF2), так как именно они характеризуются максимальными отклонениями относительных частных дисперсий PgF от нормальных прямых. Рекордсменом здесь является кристалл флюорита (фтористого кальция) с nd» 1.43 и nd» 95, для которого значение D nd на участке lg - lF составляет» +22.4. Ряд фторофосфатных и чисто фторидных «особых» кронов (включая уже упоминавшееся стекло N-FK56 из каталога фирмы Шотт) разрабатывались именно с целью максимально приблизить их оптические характеристики к свойственным флюориту и тем самым получить стеклообразные заменители последнего. Отклонения «особых» флинтов (курцфлинтов) от нормальной прямой не столь значительны (-3 > D nd ³ -7.5). Никакой спецификой химического состава они не обладают. «Особые» флинты с повышенными (D nd £ +16) значениями относительной частной дисперсии (лангфлинты) – это либо тяжелые и сверхтяжелые флинты с максимальным содержанием окиси свинца, либо титановые флинты с высоким содержанием окиси титана. Таким образом, расположение «особых» стекол на диаграмме «относительная частная дисперсия – коэффициент дисперсии» следует, строго говоря, не нормальной прямой, а некоторой кривой с очень большим радиусом кривизны. Как было показано путем моделирования значений оптических характеристик с помощью аналитической модели диэлектрической проницаемости стекол [29], геометрическим местом точек оптических стекол на этой диаграмме является не прямая, а отрезок гиперболы, которая пересекает нормальную прямую в двух точках. Поэтому «особые» свойства значительной части «особых» стекол (в том числе всех курцфлинтов) определяются чисто математическими факторами (попаданием точки на диаграмме «относительная частная дисперсия – коэффициент дисперсии» в ту или иную зону гиперболы) и не связаны напрямую с особенностями их химического состава и/или структуры. Разброс точек стекол вокруг гиперболы, являющейся их геометрическим местом, обусловлен в первую очередь вариациями вкладов колебательных возбуждений (с собственными частотами, лежащими в среднем ИК диапазоне) в значения диэлектрической проницаемости при частотах видимого диапазона. Особенностью вышеупомянутых фторидных кристаллов и фторсодержащих лангкронов являются аномально низкие значения вкладов колебательных возбуждений, что и определяет их еще более высокие относительные частные дисперсии по сравнению с ожидаемыми для такой гиперболы.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 716; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.57.5 (0.009 с.) |

 . (7.4.1)
. (7.4.1)
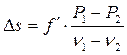 , (7.5.1)
, (7.5.1)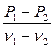 в формуле (7.5.1) есть не что иное, как тангенс угла наклона нормальной прямой на диаграмме Pl 4 l 5- nl 1, то есть величина постоянная для данной диаграммы. Отсюда следует практически важный вывод: для любой пары «нормальных» оптических материалов, точки которых лежат вокруг нормальной прямой, значение вторичного спектра D s также есть величина практически постоянная, и ее нельзя заметно уменьшить, выбирая какие угодно сочетания таких материалов. Таким образом, ахроматизацию объектива для более чем двух длин волн (то есть уменьшение вторичного спектра D s) возможно осуществить лишь за счет использования «особых» оптических материалов, точки которых достаточно существенно отклоняются от нормальной прямой. Только в этом случае можно увеличить знаменатель формулы (7.5.1), не увеличивая одновременно ее числитель (или уменьшить числитель, не уменьшая знаменатель), и тем самым снизить значение D s.
в формуле (7.5.1) есть не что иное, как тангенс угла наклона нормальной прямой на диаграмме Pl 4 l 5- nl 1, то есть величина постоянная для данной диаграммы. Отсюда следует практически важный вывод: для любой пары «нормальных» оптических материалов, точки которых лежат вокруг нормальной прямой, значение вторичного спектра D s также есть величина практически постоянная, и ее нельзя заметно уменьшить, выбирая какие угодно сочетания таких материалов. Таким образом, ахроматизацию объектива для более чем двух длин волн (то есть уменьшение вторичного спектра D s) возможно осуществить лишь за счет использования «особых» оптических материалов, точки которых достаточно существенно отклоняются от нормальной прямой. Только в этом случае можно увеличить знаменатель формулы (7.5.1), не увеличивая одновременно ее числитель (или уменьшить числитель, не уменьшая знаменатель), и тем самым снизить значение D s.


