
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Следствия неупорядоченности структуры для оптических свойствСодержание книги
Поиск на нашем сайте
Изложенное в предыдущем параграфе представляет собой лишь общую схему структуры стекла, на которую затем накладываются различного рода микроскопические флуктуации, типичные для стеклообразного состояния. Однако именно эта общая схема, а не флуктуации или иные частности, определяет принципиальные отличия оптических и спектроскопических свойств стекол. Во-первых, как уже упоминалось во введении, континуальная неупорядоченность структуры стекла обеспечивает полную изотропность всех свойств и соответственно оптическую однородность стекол, лишенных технологических дефектов. Во-вторых, континуальная неупорядоченность структуры стекла означает случайный характер электрического и силового поля, действующего на каждый электронный или колебательный осциллятор. Для электронных возбуждений, локализованных на объектах атомных размеров (ионах примесей и активаторов или на собственных точечных дефектах) это ведет к хорошо известному эффекту так называемого неоднородного уширения спектральных линий за счет случайного распределения частот соответствующих оптических возбуждений, вызываемого случайным характером упомянутых полей (см., например, [22]). Для колебательных возбуждений картина несколько более сложна, однако и в этом случае, как было показано позднее, в итоге возникает уширение спектральных полос за счет случайного распределения частот колебаний. Более подробно этот вопрос рассматривается позднее в одной из специальных дисциплин. Довольно долгое время эти эффекты не находили адекватного отражения в уравнениях для комплексной диэлектрической проницаемости. В качестве первого простейшего шага использовалось представление контура полосы поглощения с помощью плотности вероятности нормального (гауссова) распределения:
где μ - центр распределения и σ - среднеквадратичное отклонение. Величина σ2 именуется также дисперсией распределения:[16] График функции p (x) имеет вид максимума с более широкой вершиной и более крутыми крыльями, что представлялось более удобным для описания уширенных полос (см. рис. 20). Основываясь на уравнении (5.1.1), гауссов контур полосы в спектре коэффициента поглощения записывается в виде:
где роль переменной играет текущая частота w, положение центра полосы w 0 занимает место центра распределения, а среднеквадратичное отклонение σ определяет половину полуширины полосы. Однако такое переобозначение параметров носит чисто формальный характер; кроме того, такая важная характеристика оптического возбуждения, как коэффициент затухания g, определяющий время жизни возбужденного состояния, вообще не участвует в уравнении (5.1.2). Поэтому уравнение (5.1.2) следует считать чисто эмпирическим. В качестве определенного оправдания для пренебрежения участием коэффициента затухания в выражении для контура линии часто указывается предположение, что σ >> g. Тем не менее, стандартные методы разложения сложного оптического спектра на компоненты, использующие гауссов контур этих компонент, до сих пор используются достаточно широко.
Рис. 20. Форма максимумов плотности вероятности гауссова распределения при различных значениях дисперсии распределения s 2.
Помимо вышеуказанной «нефизичности» исходного уравнения (5.1.2), эти методы имеют и другой недостаток. Дело в том, что гауссовы контуры часто имеют более крутые крылья, чем полосы в разлагаемом спектре, и это создает соблазн добавлять лишние контуры в разложение для устранения слишком глубоких провалов между полосами. Для описания неоднородно уширенных полос использовались и другие (в том числе асимметричные) функции, но все они также носили эмпирический характер. 5.3. Дисперсионное уравнение для комплексной диэлектрической проницаемости стеклообразных веществ (аналитическая модель свертки) Можно достаточно строго и непротиворечиво учесть влияние распределения осцилляторов по частоте при разупорядочении материала на вид уравнения для диэлектрической проницаемости, используя классическую модель Друде (4.2.1а-в) как исходную основу. Эта возможность была впервые реализована в российских первоисточниках, цитированных в [23], и полученное дисперсионное уравнение с тех пор широко применяется для количественного описания дисперсии диэлектрической проницаемости стеклообразных веществ [8,15,16,23]. Не останавливаясь на деталях вывода этого дисперсионного уравнения, отметим здесь, что плотность вероятности гауссова распределения (5.1.1) была использована только для представления распределения числа осцилляторов каждого вида по частоте, и затем эти распределения были введены в классическую модель Друде (4.2.1а-в). Таким образом, была получена аналитическая модель дисперсии комплексной диэлектрической проницаемости, учитывающая влияние разупорядочения структуры на ширину спектральных компонент в спектрах стекол:
Говоря языком математики, уравнение (5.3.1а) содержит так называемую свертку лоренцевой и гауссовой функций. Поэтому для краткости аналитическую модель дисперсии комплексной диэлектрической проницаемости стекол, описываемую уравнением (5.3.1а), принято называть моделью свертки. Действительная и мнимая части комплексной диэлектрической проницаемости, задаваемой уравнением свертки (5.3.1а), имеют вид:
и
Таким образом, в аналитической модели свертки (5.3.1а-в) каждый осциллятор характеризуется уже четырьмя параметрами, а не тремя, как в случае классической модели Друде. При этом физический смысл некоторых параметров, присутствовавших также и в исходной классической модели, в модели свертки принципиально отличается от физического смысла параметров классической модели. Обсудим этот вопрос более подробно. Два параметра сохраняют в модели свертки (5.3.1а-в) точно тот же физический смысл, что и в исходной классической модели (4.2.1а-в). Это - абсолютная интенсивность j -го осциллятора (оптического возбуждения) Sj и коэффициент затухания осциллятора g j. Напротив, физический смысл параметра, сохраняющего обозначение w j, принципиально изменяется. Напомним, что w j в исходной классической модели (4.2.1а-в) - это собственная частота осциллятора (частота его оптического возбуждения). Однако при переходе к модели свертки собственная частота осциллятора вообще исчезает как постоянный параметр. Как видно из уравнений (5.3.1а-в), собственные частоты всех осцилляторов превращаются в единую переменную интегрирования x. Таким образом, обозначение w j присваивается по сути дела новому параметру; таким параметром является центральная частота непрерывного распределения осцилляторов. Идентичность обозначения центра распределения осцилляторов в модели свертки (5.3.1а-в) тому, которое использовалось для собственной частоты осцилляторов в классической модели (4.2.1а-в), была сохранена ради того, чтобы в обоих случаях символ w j соответствовал примерному положению центра максимума мнимой части комплексной диэлектрической проницаемости. Наконец, новый четвертый параметр s j, появляющийся в модели свертки – это среднеквадратичное отклонение для непрерывного распределения осцилляторов, характеризующее половину полуширины максимума этого распределения. Рис. 21 и 22 показывают, как влияет переход от лоренцева осциллятора, описываемого классической моделью Друде (4.2.1а-в), к осциллятору, описываемому моделью свертки (5.3.1а-в), на контуры показателя преломления, показателя поглощения, действительной и мнимой частей комплексной диэлектрической проницаемости. Расчет в модели свертки выполнялся для значения s / w 0, равного 0.035, которое достаточно типично для фундаментальных ИК спектров стекол. Как видно из рис. 21, модель свертки (5.3.1а-в) дает очень значительное уширение центральных частей контуров e¢(w) и e¢¢(w) по сравнению с классической моделью Друде (4.2.1а-в). В результате такого уширения минимум e¢(w) перестает достигать области отрицательных значений. В спектрах n(w) и k(w), рассчитанных с помощью модели свертки (5.3.1а-в), также наблюдается сильное уширение контуров вокруг точки w = w 0 (см. рис. 21), тогда как на крыльях различия между значениями n(w) и k(w), вычисляемыми с помощью сравниваемых моделей, становятся несущественными уже при значениях w / w 0 порядка 0.85 или 1.15. Такое уширение спектральных контуров оптических постоянных преимущественно вокруг точки w = w 0 очень хорошо соответствует реальному характеру уширения полос в экспериментальных спектрах стекол. Как будет показано ниже (см. параграф 6.2), только модель свертки (5.3.1а-в) позволяет столь точно описывать экспериментальные спектры отражения и поглощения стекол, что все отклонения расчетного спектра от экспериментального укладываются в пределы погрешности измерения. Напротив, применение к стеклам классических моделей Друде или Лоренц-Лорентца (а также иных моделей, предназначенных для кристаллов) ведет к расхождениям расчета и эксперимента, далеко выходящим за пределы погрешности измерения.
Рис. 21. Сравнение контуров действительной и мнимой частей комплексной диэлектрической проницаемости вблизи частоты w 0 единственного осциллятора при значениях s / w 0, равных нулю и 0.035. Значения S / w 02, g / w 0 и
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 427; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.119.163 (0.006 с.) |

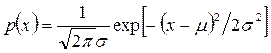 , (5.1.1)
, (5.1.1)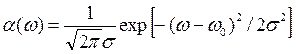 , (5.1.2)
, (5.1.2)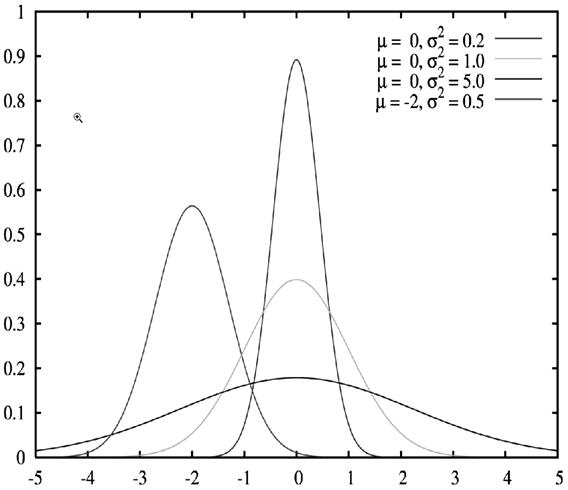
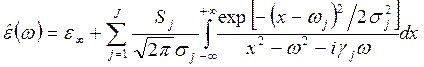 . (5.3.1а)
. (5.3.1а)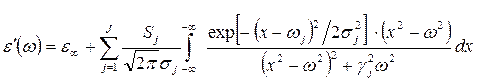 , (5.3.1б)
, (5.3.1б)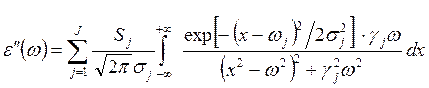 . (5.3.1в)
. (5.3.1в)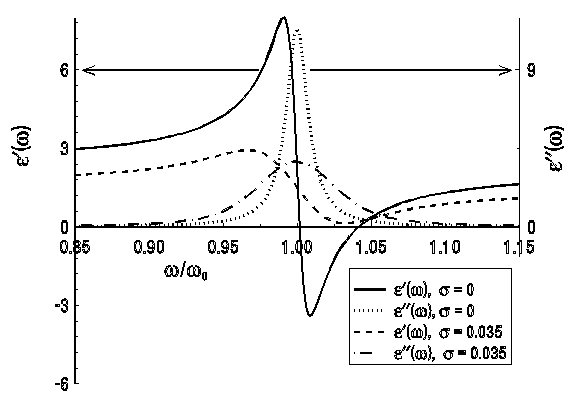
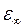 те же, что и на рис. 15.
те же, что и на рис. 15.


